Обобщенная теорема Чебышева

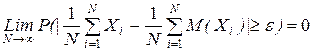, X_i - i-ая случайная величина

Теорема Маркова. Обобщенная теорема Чебышева справедлива и для зависимых случайных величин, если

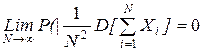
Центральная предельная теорема. Если X₁ , X₂,..., X_n - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(X_i)=a и дисперсию s², то при N ® ¥ закон распределения суммы 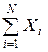неограниченно приближается к нормальному:

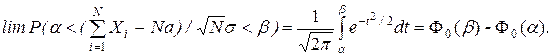
Приведем пример применения методов статистического моделирования.

Пример. Проводится s=10 независимых выстрелов по мишени, причем вероятность попадания при одном выстреле задана и равна p. Требуется оценить вероятность того, что число попаданий в мишень будет четным.

Аналитическое решение этой задачи:

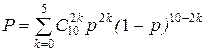
Схема алгоритма (статистическое моделирование) (рис. 12):

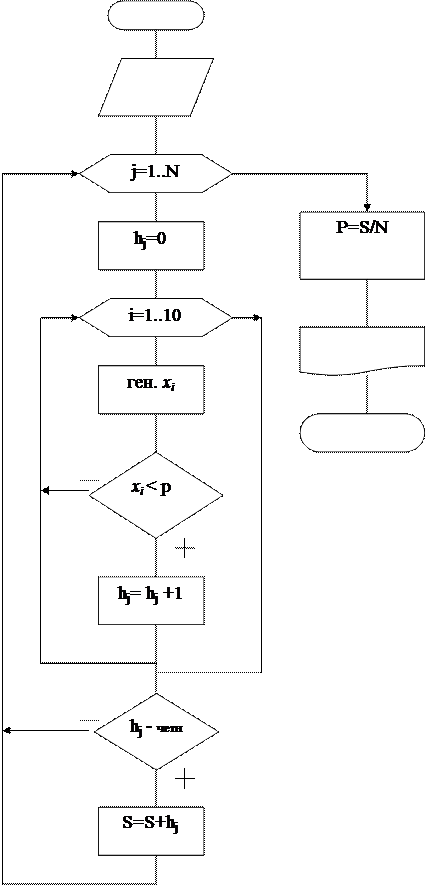
Рис. 12.

8.2. Обработка результатов моделирования

В процессе имитационного моделирования формируется большое количество реализаций, являющихся исходным статистическим материалом для нахождения приближенных значений показателей эффективности или, как говорят, их оценок.

Оценкой вероятности является частота 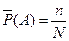. Для ее получения обычно организуют на программном уровне 2 счетчика: один для подсчета общего количества экспериментов N, второй – для подсчета количества положительных исходов n.

В качестве характеристик исследуемой системы выступает закон плотности распределения. Его приближенно можно охарактеризовать гистограммой. Для этого интервал измерения СВ разбивают на отрезки 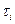, каждому из них сопоставляют счетчик, где накапливают 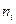- количество попаданий значений СВ в 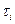. На каждом 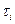строится прямоугольник с высотой 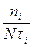. Полученную гистограмму можно сгладить.

Оценку математического ожидания получают как среднее арифметическое значение y_i СВ

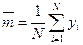
Оценку дисперсии можно вычислять по формуле

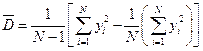
Определение объема выборки.

Объем выборки – это количество реализаций, которое необходимо при имитационном моделировании, чтобы обеспечить стохастическую точность результата.

При вычислении оценки математического ожидания с заданной точностью и достоверностью объем выборки можно вычислить по формуле:

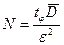
Здесь: 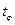- квантиль нормального распределения вероятностей порядка

;

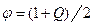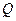- уровень достоверности;

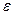- заданная погрешность, с которой необходимо получить оценку математического ожидания.

Здесь 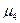- центральный момент четвертого порядка случайно величины.

Количество реализаций для получения оценки 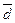с заданной точностью 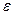можно вычислить по формуле:

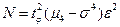
Здесь 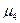- центральный момент четвертого порядка СВ

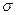- среднеквадратическое отклонение: .

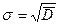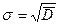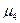Как видно из приведенных формул (2) – (5), для их практического использования необходимо знать и , которые как правило бывают неизвестными. В этом случае используют вместо точных значени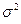й и 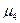их оценки, получаемые предварительно при некотором N. Если при этом заданная точность 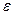не достигнута, то N увеличивают, после чего проводится уточнение оценок. Этот процесс повторяется до тех пор, пока заданная точность будет обеспечена.

Критерий согласия хи-квадрат (Пирсона).

При обработке результатов машинного эксперимента с моделью системы часто возникает задача определения эмпирического закона распределения случайной величины. Общая схема решения этой задачи сводится к тому, что:

· строят по результатам имитационного эксперимента гистограмму (оценку функции плотности распределения вероятностей);

· выдвигают гипотезу о согласии эмпирического закона с каким-либо теоретическим распределением;

· проверяют гипотезу с помощью одного из статистических критериев согласия (Пирсона, Колмогорова, Смирнова и т.д.

В качестве критерия проверки гипотезы по методу Пирсона выбирают величину, которая характеризует степень расхождения эмпирического и теоретического закона следующим образом:

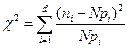
где: 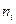- количество значений случайной величины 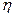, попавших в i – ый подынтервал;

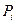- вероятность попадания случайно величины 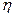в i – ый подынтервал;

d- количество подынтервалов, на которые разбивается интервал измерения в имитационном эксперименте.

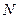- объем наблюдений.

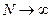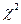
При закон распределения величины хи-квадрат, являющейся мерой расхождения, зависит только от количества подынтервалов и приближается к закону распределения с 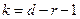степенями свободы, где 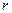- число параметров теоретического закона распределения. Функция распределения 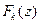величины 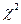табулирована

Проверка гипотезы о согласованности эмпирического и теоретического законов распределения с помощью критерия согласия Пирсона осуществляется в последовательности:

1.Результаты наблюдений 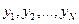группируют в интервальный вариационный ряд. Объем наблюдений должен быть достаточно большим ( 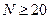). Если частота, соответствующая какому-либо интервалу, окажется меньше 5, то интервал объединяют с соседним, так, чтобы частота попадания значения случайной величины в подынтервал была бы больше или равна 5.

2.Выдвигают гипотезу о виде распределения по виду гистограммы.

3.Задают уровень значимости .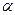

4.Определяют теоретическую вероятность 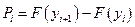попадания случайно величины 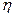в каждый из подинтервалов.

5.Вычисляют величину расхождения законов .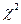

6.Определяют число степеней свободы .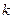

7.По вычисленным значениям 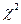и 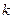по таблицам находят вероятность 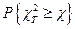. Если она превышает уровень значимости 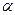, то считают, что гипотеза о виде распределения отвергается.

9. Элементы теории Марковских случайных процессов, используемые при моделировании систем

9.1. Потоки событий

Одним из важных понятий, используемых при моделировании систем является понятие потока событий, который поступает на вход системы.