Переходная характеристика в форме Баттерворта

p² + 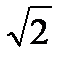w₀ p + w₀² = 0

где Ö2 w₀ = 1 / Т_тп ; К_S = 1/ Т_тп ; К_р = К_S / К_н

ПРИМЕР 2.

САР частоты вращения двигателя постоянного тока, управляемого тиристорным преобразователем по цепи возбуждения при условии I_я = const.

Передаточная функция неизменяемой части системы равна

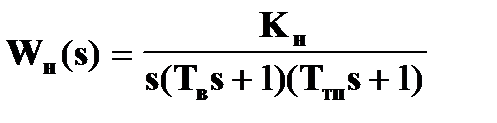
где К_н - коэффициент передачи неизменяемой части САР,

К_н = К_д К_тп К_тг К_п / J ,

J - суммарный момент инерции якоря двигателя и приводного механизма,

Т_в , Т_тп - постоянные времени обмотки возбуждения и тиристорного преобразователя.

Так как объект регулирования по цепи управления в данном случае является астатическим, то для получения астатизма по цепи возмущения необходимо ввести ПИД - регулятор для компенсации постоянной времени обмотки возбуждения и устранения неустойчивости замкнутой САР со стороны задающего воздействия, т.е.

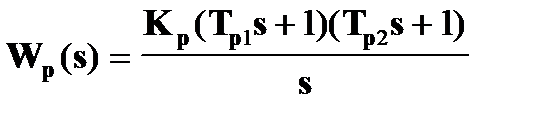
Если Т_р1 = Т_в , то передаточная функция разомкнутой САР будет

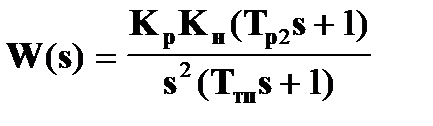
а передаточная функция замкнутой САР по управлению

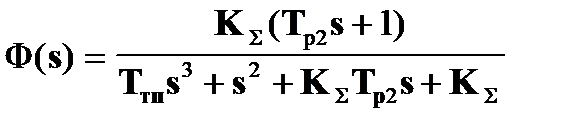
Характеристическое уравнение замкнутой САР

p³ + A₁ w₀ p² + A₂ w₀² p + w₀³ = 0,

где A₁ w₀ = 1 / T_тп , A₂ w₀² = K_S T_p2 / T_тп , w₀³ = К_S / T_тп

1. Биномиальная форма переходной характеристики

p³ + 3 w₀ p² + 3 w₀² p + w₀³ = 0

Тогда 3w₀ = 1 / T_тп , 3 w₀² = К_S Т_р2 / T_тп , w₀³ = K_S / T_тп

К_S = 1 / (27 T_тп²) , Т_р2 = 9Т_тп

2. Переходная характеристика по минимуму среднеквадратичной ошибки

p³ + w₀ p² + 2 w₀² p + w₀³ = 0

Тогда w₀ = 1/ T_тп , 2 w₀² = K_S T_p2 / T_тп , w₀³ = K_S / T_тп

К_S = 1 / T_тп² , Т_p2 = 2 Т_тп

3. Переходная характеристика в форме Баттерворта

p³ + 2 w₀ p² + 2 w₀² p + w₀³ = 0

Тогда 2 w₀ = 1 / T_тп , 2 w₀² = K_S T_p2 / T_тп , w₀³ = K_S / T_тп

К_S = 1/ (8 T_тп²) , Т_p2 = 4 Т_тп

ПРИМЕР 3.

САР напряжения генератора постоянного тока.

Передаточная функция неизменяемой части системы равна

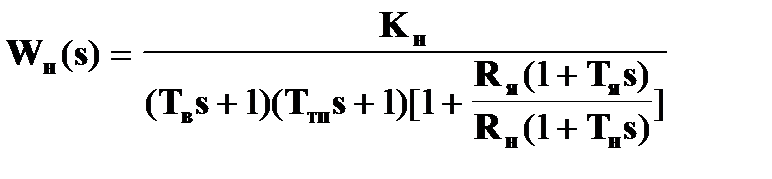
где К_н - коэффициент передачи неизменяемой части САР,

К_н = К_г К_тп К_п ,

К_г - коэффициент передачи генератора,

К_тп - коэффициент передачи тиристорного преобразователя,

К_п - коэффициент передачи потенциометра,

Т_в ,Т_тп ,Т_я ,Т_н - постоянные времени обмотки возбуждения, тиристорного преобразователя, якоря генератора и нагрузки, соответственно.

Так как Т_я и Т_н значительно меньше Т_в и Т_тп ,то ими можно пренебречь.

Тогда выбираем ПИ - регулятор для компенсации наибольшей постоянной времени Т_в и введения астатизма, т.е.

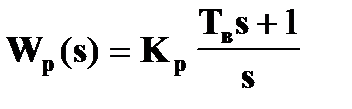
Передаточная функция разомкнутой САР будет

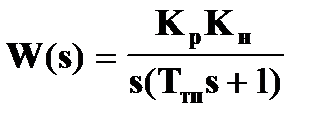
Расчет параметров регулятора проводится аналогично первому примеру.

ПРИЛОЖЕНИЕ

Формулы для расчета переходных процессов.

1. Для случая кратных корней (биномиальные формы):

n = 2 p² + 2w₀p + w₀² = 0

p₁ = p₂ = - w₀

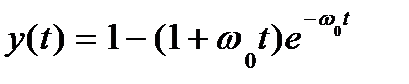
n = 3 p³ + 3w₀ p² + 3w₀² p + w₀³ = 0

p₁ = p₂ = p₃ = - w₀

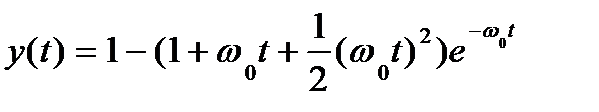
n = 4 p⁴ + 4 w₀ p³ + 6 w₀² p² + 4 w₀³ p + w₀⁴

p₁ = p₂ = p₃ = p₄ = - w₀

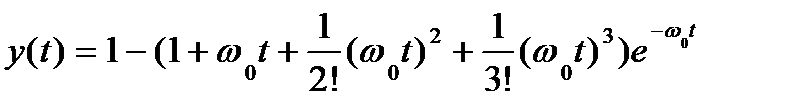
2. Минимум среднеквадратичной ошибки:

n = 2 p² + w₀ p + w₀² = 0

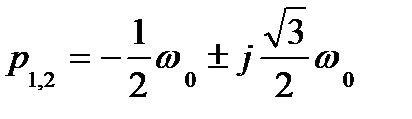
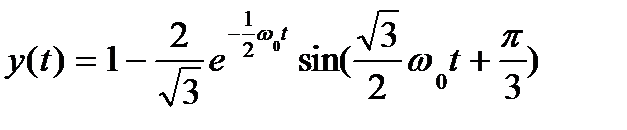
n = 3 p³ + w₀ p² + 2 w₀² p + w₀³ = 0

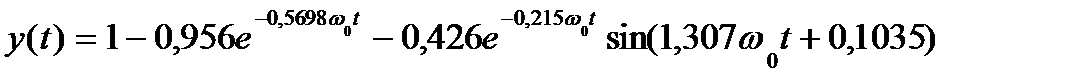
3. Оптимум по модулю (форма Баттерворта):

n = 2 p² + Ö2 w₀ p + w₀² = 0

p_1,2 =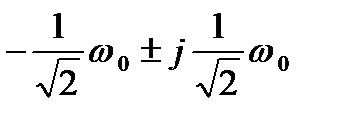

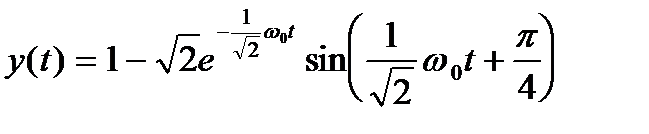
n = 3 p³ + 2w₀ p² + 2 w₀² p + w₀³

p₁ = - w₀ ; p_2,3 =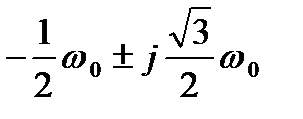

y(t)= 1 -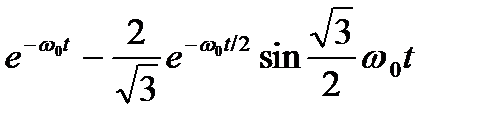

n = 4 p⁴ + 2,6 w₀ p³ + 3,4 w₀² p² + 2,6 w₀³ p + w₀⁴ = 0

p_1,2 = -0,9239 w₀ ± j 0,3827 w₀; p_3,4 = -0,3827w₀ ± j 0,9239 w₀

y(t) = 1 - 2,4142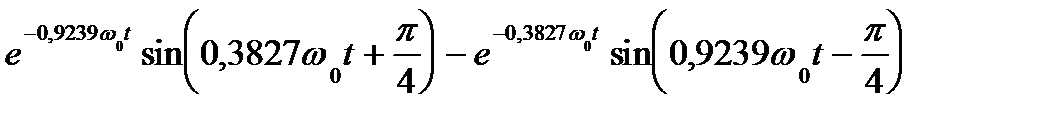

ЛИТЕРАТУРА

1. Тимофеев Ю.К., Крылов А.П. Линейные системы автоматического управления: Учебн.пособие.-СПб.: Изд-во ГМА им.адм. С.О.Макарова, 2008. -190 с.

2. Ерофеев А.А. Теория автоматического управления: Учебник для вузов.-СПб.: Политехника, 2008. -302 с.

3. Сборник задач по теории автоматического регулирования и управления /Под ред. В.А.Бесекерского . Наука.: 1978.- 512 с.

4. Башарин А.В., Голубев Ф.Н., Кепперман В.Г. Примеры расчетов автоматизированного привода. – Л.: Энергия, 1971.- 440 с.