Границе раздела сред

Выясним как изменяются векторы электромагнитного поля вблизи раздела границы двух сред, полагая, что эту границу с достаточной степенью точности можно считать симметричной. Не будем интересоваться свойствами электромагнитного поля в переходном слое границ.

Рассмотрим первое из уравнений Максвелла в интегральной форме:

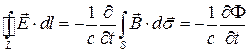
Применим его к бесконечно малому контуру 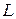, изображённому на рисунке:

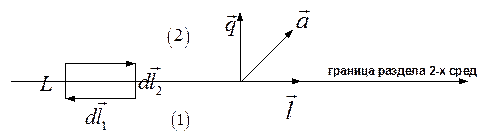
Будем считать сторону 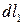бесконечно малой 1-го порядка малости, а 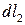бесконечно малой 2-го порядка малости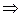

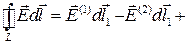бесконечна малая 2-го порядка

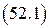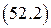Уравнения и дают:

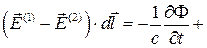бесконечно малая 2-го порядка.

Т.к. 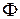- поток через поверхность контура 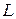и он пропорционален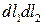 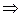он является величиной более чем 2-го порядка малости.

Т.к. 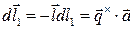, то

.

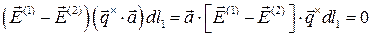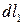
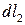
Переходя к пределу 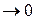и ориентация 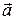произвольна:

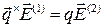
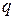- единичный вектор границы раздела.

Применим аналогичный приём к формулам:

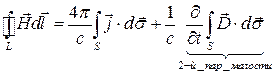
Опустив член 2-го порядка малости, тогда

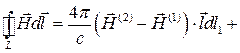б.м. 2-го порядка малости

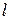- единичный вектор контура, лежащий в плоскости раздела.

Пусть 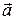- нормаль к поверхности, охваченной контуром 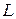, тогда 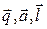связаны соотношением: .

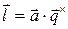Введём понятие поверхностной плотности тока – количество электричества, проходящего в единицу времени через единичную поверхность

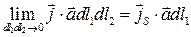
Тогда 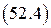даёт: .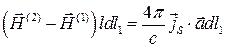

Учитывая произвольность ориентации 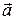в плоскости границы раздела получим:

Туту какая-то лажа..

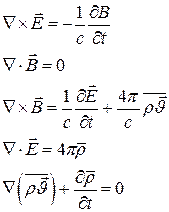
Для того чтобы найт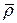и и 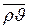требуется ввести некоторые допущения о строении вещества. В теории электромагнитного поля в веществе последняя рассматривается как сплошная среда, свойства которой описываются рядом параметров, макроскопических характеристик: проницаемость, проводимость и т.д.

Окончательное выражение:

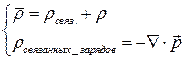
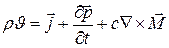
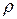и 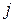объёмная плотность свободных зарядов и плотность тока свободных зарядов. Они не связаны с атомами вещества и не индуцируются полем.

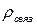- объёмная плотность связанных зарядов, т.е. зарядов входящих в состав атомов, молекул, расположенных в углах кристаллической решетки и потому не способных к свободному перемещению.

Среды, в состав которых входят только связанные заряды называются диэлектрическими.

В состав проводящих сред входят свободные заряды, способные свободно перемещаться в пределах данной среды.

Если свободный заряд поместить на диэлектрик, то его конфигурация сохраняется на диэлектрике определённо долго.

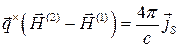
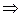при наличии поверхностных токов, поверхностная плотность претерпевает разрыв.

Граничные условия для нормальных составляющих векторов 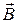и 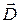получаются из уравнений Максвелла 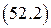и 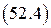, если выбрать малую поверхность.

Площадь оснований 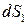б.м. 1-го порядка, а 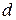(площадь боковой грани) – б.м. 2-го порядка 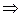из уравнений Максвела

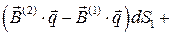б.м. 2-го порядка .

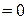Переходим к пределу и находим:

.

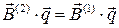Аналогично, из последнего уравнения Максвела находим:

,

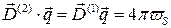где поверхностная плотность заряда 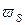определяется:

.
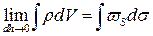