Взаимное расположение прямой и плоскости.

Лекция 7 Плоскость и прямая в пространстве.

Уравнения плоскости в пространстве.

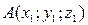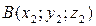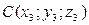1. Общее уравнение плоскости.Пусть плоскость задана тремя точками , и . Тогда ее уравнение имеет вид:

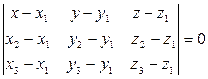. (7.1)

Разложив определитель (7.1) по первой строке, получим уравнение:

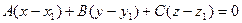, (7.2)

где , , .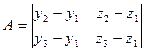

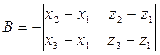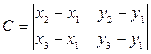Раскрыв скобки в уравнении (7.2) и обозначив 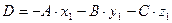, получим общее уравнение плоскости: 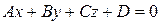. (7.3)

Другие формы уравнения плоскости.

а) Уравнение плоскости, проходящей через точку 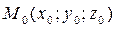и перпендикулярно к вектору 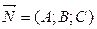, имеет вид: 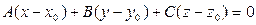. (7.4)

Вектор 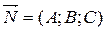называется нормальным вектором плоскости.

б) Уравнение плоскости в отрезках на осях: 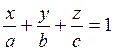, (7.5)

где 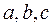– длины отрезков, отсекаемых на координатных осях, взятые с соответствующими знаками.

в) Нормальное уравнение плоскости: 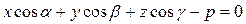, (7.6)

где 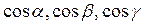– направляющие косинусы перпендикуляра, проведенного из начала координат к данной плоскости, а 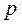– его длина.

Для приведения общего уравнения плоскости (7.3) к нормальному виду (7.6), следует умножить (7.3) на нормирующий множитель 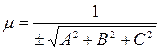, где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.

Угол между плоскостями.

Условия перпендикулярности и параллельности плоскостей.

Расстояние от точки до прямой.

Угол 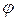между плоскостям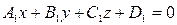и и 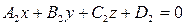определяется по формуле: 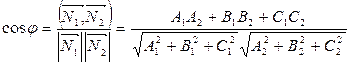. (7.7)

Условием параллельности плоскостей является: 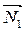|| 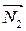, 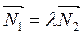или в координатной форме 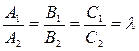. (7.8)

Условием перпендикулярности двух плоскостей будет 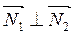, т.е. 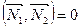или в координатной форме: 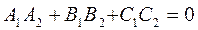. (7.9)

Расстояние d от данной точки 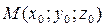до плоскости, заданной уравнением 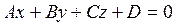, находится по формуле:

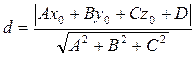. (7.10)

Прямая в пространстве.

Прямую в пространстве можно представить как пересечение двух плоскостей, поэтому аналитически ее можно задать системой двух линейных уравнений вида:

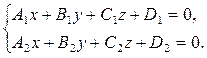(7.11)

Система (7.11) определяет прямую только в том случае, когда коэффициенты 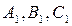не пропорциональны коэффициентам 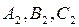и называется общими уравнениями прямой.

Канонические уравнения прямой 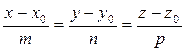(7.12)

определяют прямую, проходящую через точку 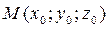параллельно вектору 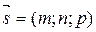, который называется направляющим вектором прямой.

Параметрические уравнения прямойимеют вид: 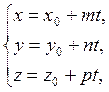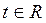. (7.13)

Угол между прямыми.

Взаимное расположение прямых в пространстве.

Угол между прямым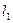и и 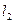, заданными каноническими уравнениям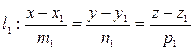и и 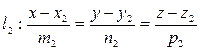, (7.14)

находится по формуле: 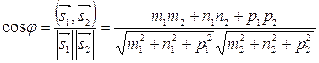. (7.15)

Условие параллельности двух прямых 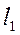и 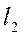записывают в виде:

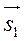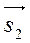|| или 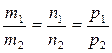. (7.16)

Условие перпендикулярности двух прямых 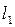и 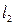записывают в виде:

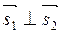, т.е. 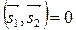, 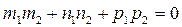. (7.17)

Прямые называются компланарными, если они лежат в одной плоскости. Необходимое и достаточное условие компланарности двух прямых, заданных каноническими уравнениями, записывают в виде:

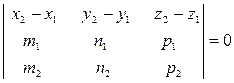. (7.18)

Если условие (7.18) не выполняется, то прямые скрещиваются.

Взаимное расположение прямой и плоскости.

Возможны следующие случаи расположения прямой и плоскости:

1) Прямая параллельна плоскости.

Условие параллельности прямой 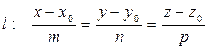и плоскости 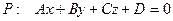(рис. 7.1) означает, что 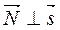, т.е. 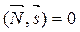или 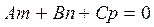. При этом .

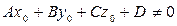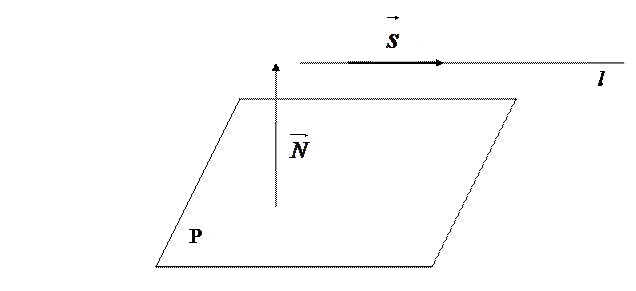
Рис. 7.1

2) Прямая лежит в плоскости.

Условие того, что прямая l лежит в плоскости P означает, что точка 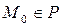и 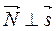(рис. 7.2), откуда имеем: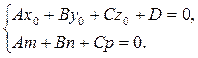

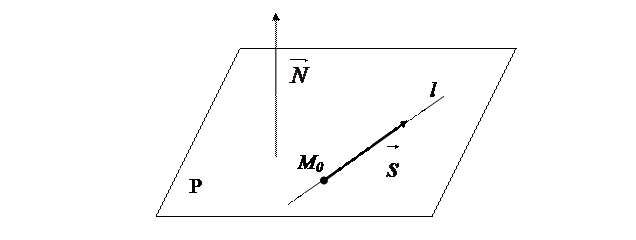
Рис. 7.2

3) Прямая пересекает плоскость, если 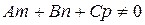.Для определения точки пересеченияпрямой 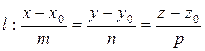с плоскостью 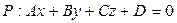надо совместно решить их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой (7.13). В этом случае из уравнения 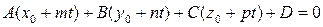находим значение параметра t, соответствующее точке пересечения. Подставляя значение t в параметрические уравнения прямой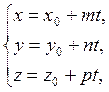 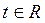, получаем координаты точки 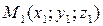пересечения прямой и плоскости.

Частным случаем пересечения прямой и плоскости является их перпендикулярность.

Условие перпендикулярности прямой l и плоскости P (рис.7.3) означает, что 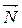|| 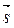, т.е. 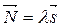или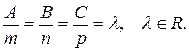

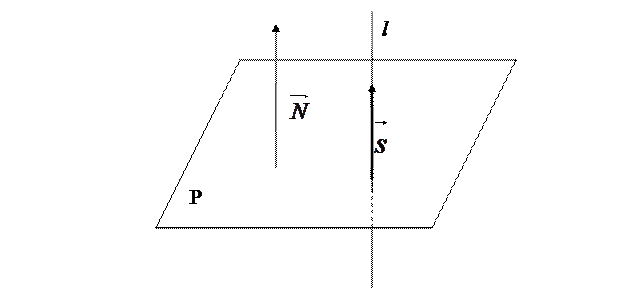
Рис. 7.3

Угол между прямой 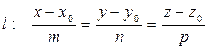и плоскостью 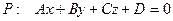находится по формуле:

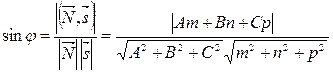, (7.19)

где 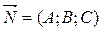; 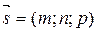(рис. 7.4)

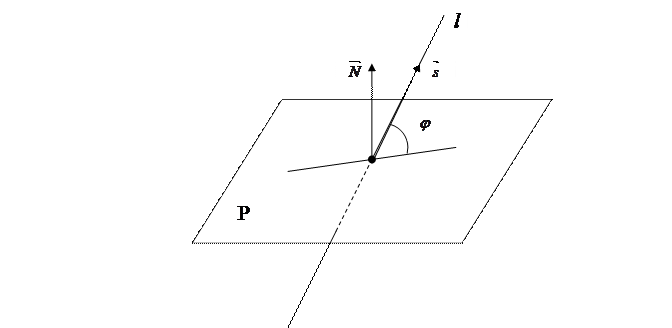
Рис.7.4