II. Решение систем уравнений с помощью обратной матрицы
Сведения из теории.  Система n линейных алгебраических уравнений с n неизвестными имеет такой вид:
Система n линейных алгебраических уравнений с n неизвестными имеет такой вид:
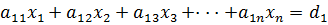 ; ; 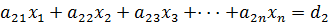 ; ; 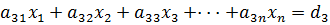 ; ;  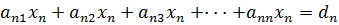 . . | (4.1) |
Мы будем рассматривать только такие системы линейных алгебраических уравнений, у которых число уравнений равно числу неизвестных. В системе уравнений (4.1) неизвестными являются 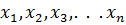 , а коэффициенты
, а коэффициенты 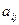
(i, j = 1, 2, 3, 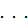 n) при неизвестных и свободные члены di (i = 1, 2, 3,
n) при неизвестных и свободные члены di (i = 1, 2, 3, 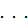 n) – действительные числа.
n) – действительные числа.
Составим матрицу А из коэффициентов 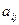 при неизвестных, а также матрицу-столбец х из неизвестных и матрицу-столбец d из свободных членов
при неизвестных, а также матрицу-столбец х из неизвестных и матрицу-столбец d из свободных членов
А = 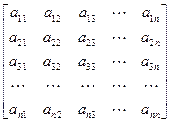 ,
,
x = 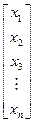 ; d =
; d = 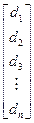 .
.
Учитывая правило умножения матриц и условие равенства двух матриц, систему (4.1) можно записать в виде
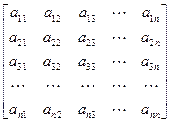 · · 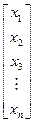 = = 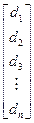 | (4.2) |
или, учитывая введенные обозначения, всю систему уравнений (4.2) можно записать компактно в виде одного матричного уравнения.
| Аx = d. | (4.3) |
Такая запись большого числа линейных уравнений в виде одного уравнения является одним из достоинств матричных обозначений.
На предыдущем практическом занятии мы уделили большое внимание вычислению обратной матрицы. Покажем теперь применение этой операции для решения системы линейных алгебраических уравнений.
Если матрица А – неособенная, то она имеет обратную матрицу 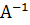 . Умножим слева обе части уравнения (4.3) на
. Умножим слева обе части уравнения (4.3) на 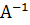 и заметив, что
и заметив, что 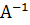 · А = Е – единичная матрица, получим столбец неизвестных х из равенства
· А = Е – единичная матрица, получим столбец неизвестных х из равенства
x = 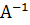 d. d. | (4.4) |
В этой формуле х может быть не только матрицей-столбцом, но и матрицей размера n × m. В этом случае и матрица d составленная из свободных членов, должна тоже иметь размер n × m.
Таким образом, нам стоит только определить элементы 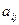 (i, j = 1, 2,
(i, j = 1, 2, 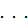 n) обратной матрицы
n) обратной матрицы 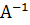 , и задачу определения неизвестных систем (4.1) можно считать решенной. Несколько таких упражнений мы выполним в начале этого практического занятия.
, и задачу определения неизвестных систем (4.1) можно считать решенной. Несколько таких упражнений мы выполним в начале этого практического занятия.
Но здесь же следует заметить, что в случае большого числа n неизвестных вычисление элементов обратной матрицы становится громоздким и затруднительным. Поэтому формула (4.4) имеет больше теоретическое значение, чем практическое, так как по сравнению с формулами Крамера для решения системы линейных алгебраических уравнений она никаких преимуществ в вычислениях не дает.
Эта формула оказывается безусловно полезной тогда, когда рассматриваются такие системы уравнений, у которых матрица коэффициентов при неизвестных одна и та же (такие системы уравнений встречаются, например, в строительной механике). Вычисление обратной матрицы в таком случае приносит большую экономию в вычислительной работе.
Это практическое занятие проведем в таком порядке: сначала будем решать системы уравнений с небольшим числом неизвестных (два, три) по формуле (4.4), а потом укажем удобную компактную схему решения системы (4.1) методом исключения (алгоритм Гаусса), которому дадим матричную трактовку.
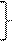 Задача 4.1 Записать систему уравнений
Задача 4.1 Записать систему уравнений
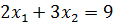 ;
;
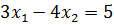
в виде одного матричного уравнения и решить ее по формуле (4.4).
Решение. Систему представим в виде
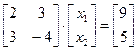 .
.
Здесь матрица
А = 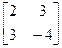 .
.
Найдем обратную ей матрицу по формуле (2.2), ПЗ 2, которая в развернутом виде выглядит так:
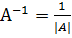 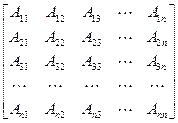 , , | (4.5) |
Где |A| - определитель матрицы А, а элементы 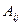 - алгебраические дополнения ее элементов
- алгебраические дополнения ее элементов 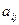 , причем матрица в правой части формулы (4.5) есть союзная матрица
, причем матрица в правой части формулы (4.5) есть союзная матрица 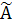 для А. Но здесь еще раз подчеркнем, что когда n > 3, то формулой (4.5) для обращения обыкновенно не пользуются, а применяют методы, рассмотренные на предыдущих практических занятиях.
для А. Но здесь еще раз подчеркнем, что когда n > 3, то формулой (4.5) для обращения обыкновенно не пользуются, а применяют методы, рассмотренные на предыдущих практических занятиях.
Воспользуемся формулой (2.2) для определения обратной матрицы
|A| = 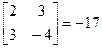 ;
;
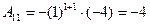 ;
; 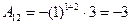 ;
;
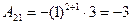 ;
; 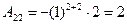 .
.
Составим матрицу, союзную матрице А
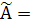
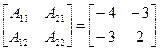 ,
,
и поэтому по формуле (2.2)
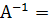
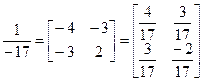 ,
,
Теперь по формуле (4.4)
x = 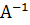 d.
d.
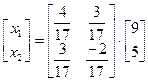
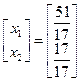 ;
;
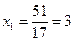 ;
; 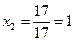 .
.
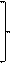 Задача 4.2 Решить систему уравнений
Задача 4.2 Решить систему уравнений
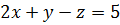 ;
;
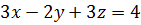 ;
;
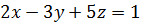 .
.
пользуясь формулой (7.4).
Решение. Запишем систему в виде одного матричного уравнения
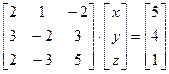 .
.
Здесь матрица коэффициентов
А = 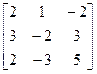 ,
,
а неизвестные x, y и z найдутся из формулы
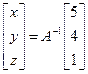 .
.
Обратим матрицу А, для чего применим формулу (2.7)
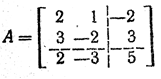 |
Здесь
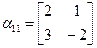 ;
; 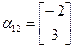 ;
; 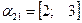 ;
; 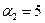 .
.
1) 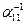 находим непосредственно
находим непосредственно
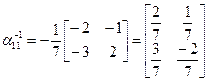 ;
;
2) 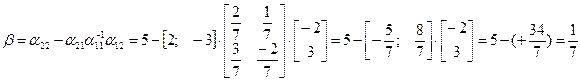
Итак, 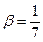 ;
; 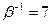 .
.
3) 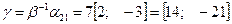 .
.
4) 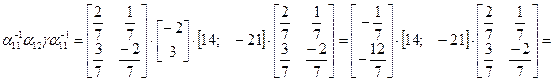
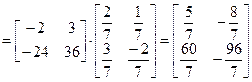 ;
;
5) 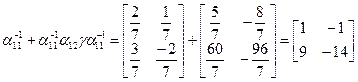 ;
;
6) 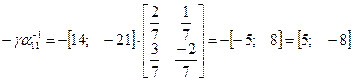 ;
;
7) 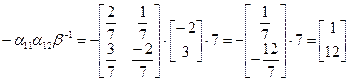 .
.
Теперь все элементы обратной матрицы известны и по формуле (2.7)
А-1 = 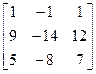 .
.
Заметим, что вычисление по формуле (2.2) оказалось бы более громоздким. Следовало бы вычислить 9 определителей второго, один определитель третьего порядка и образовать союзную матрицу А.
Подставляя матрицу А-1 в формулу (а), получим
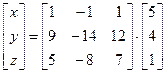 ,
,
откуда
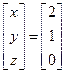 ,
,
т. е. x = 2; y = 1; z = 0.
Задача 4.3 Решить системы уравнений
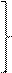
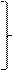
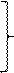 1)
1) 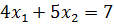 ; 2)
; 2) 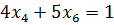 ; 3)
; 3) 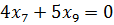 ;
;
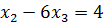 ;
; 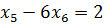 ;
; 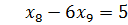 ;
;
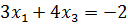 ;
; 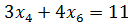 ;
; 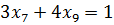 .
.
Решение. Запишем все три системы в виде одного матричного уравнения
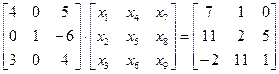 .
.
Из этого следует, что матрица неизвестных
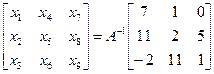 ,
,
где 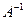 - обратная матрица для матрицы коэффициентов
- обратная матрица для матрицы коэффициентов
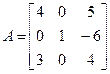 .
.
Найдем для этой матрицы обратную. В данном случае, учитывая характер этой матрицы, удобнее воспользоваться общей формулой (2.2) для определения обратной матрицы. Определитель матрицы А
|A| =1.
Алгебраические дополнения
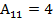 ; ; | 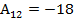 ; ; | 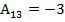 ; ; |
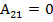 ; ; | 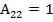 ; ; | 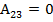 ; ; |
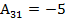 ; ; | 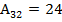 ; ; | 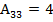 . . |
Составляем матрицу из алгебраических дополнений
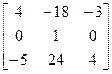 ,
,
транспонируем ее, чтобы получить союзную матрицу 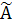 и делим на |A| = 1. Учитывая, что на основании формулы (2.2)
и делим на |A| = 1. Учитывая, что на основании формулы (2.2)
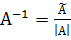 ,
,
получаем
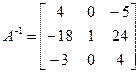 .
.
Из равенства (а) следует, что
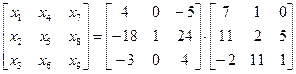 .
.
Отсюда, выполняя умножение матриц в правой части, получаем
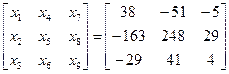 ,
,
Учитывая условия равенства матриц, находим
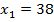 ; ; | 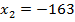 ; ; | 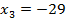 ; ; |
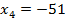 ; ; | 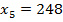 ; ; | 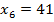 ; ; |
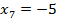 ; ; | 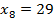 ; ; | 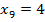 . . |
Отметим безусловную выгоду, которую мы извлекли, применяя в данном случае определение обратной матрицы и используя формулу (4.4). Если бы эти системы решать по формулам Крамера, то пришлось бы вычислять 10 определителей третьего порядка. Однако подчеркнем, что экономия в вычислениях получилась вследствие того, что матрица коэффициентов во всех трех системах была одной и той же.
IV. Алгоритм Гаусса (компактная схема)
Сведения из теории. Из большого числа известных методов решения систем линейных алгебраических уравнений мы будем пользоваться только одним из наиболее распространенных методов – методом исключения, который обычно называется методом Гаусса.
Метод Гаусса в матричном виде позволяет указать удобную для практики компактную схему решения, которая сводиться к представлению матрицы коэффициентов в виде произведения двух треугольных матриц, а эту задачу мы уже подробно разобрали на предыдущем практическом занятии.
В матричном виде система линейных алгебраических (4.1) записывается так (4.3):
Ах = d,
где А – матрица коэффициентов системы (4.1)
Представим матрицу А в виде произведения нижней треугольной матрицы С на верхнюю треугольную матрицу В, причем интересующие нас формулы выведем применительно к случаю, когда диагональные элементы матрицы В равны 1.
А = СВ
Тогда уравнение (4.3) запишется в виде
| СВх = d. | (4.6) |
Произведение Вх матрицы В на х – матрицу-столбец неизвестных, - будет матрицей-столбцом, который мы обозначим через y
| Вх = y. | (4.7) |
Уравнение (4.6) перепишется в виде
| Сy = d. | (4.8) |
После того, как из уравнения (4.8) будет определена матрица-столбец y, из уравнения (4.7), в котором, таким образом, правая часть окажется известной, можно определить матрицу-столбец x, чем и закончится решение задачи.
Распишем подробно уравнение (4.8), учитывая, что С – нижняя треугольная матрица:
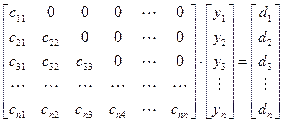 | (4.9) |
Здесь элементы 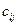 (i, j = 1, 2,
(i, j = 1, 2, 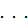 , n) известны, так как матрица А коэффициентов при неизвестных считается уже разложенной на произведение двух треугольных матриц С и В.
, n) известны, так как матрица А коэффициентов при неизвестных считается уже разложенной на произведение двух треугольных матриц С и В.
 Перемножив матрицы в левой части (4.9) с учетом условия равенства двух матриц, получаем такие уравнения для определения неизвестных
Перемножив матрицы в левой части (4.9) с учетом условия равенства двух матриц, получаем такие уравнения для определения неизвестных 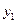 ,
, 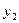 . . . ,
. . . , 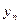 :
:
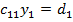 ; ; 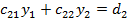 ; ; 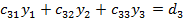 ; ; 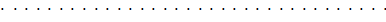 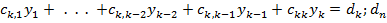 . . 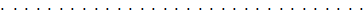 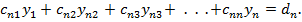 | (4.10) |
Из этой системы уравнений, начиная с первого, получаем значения неизвестных 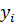 :
:
из 1- го уравнения 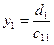 ;
;
из 1- го уравнения 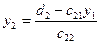 ;
;
из 1- го уравнения 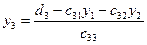 ;
;
из k - го уравнения
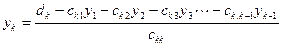
и, наконец, из n-ого уравнения
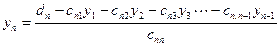 .
.
Все эти уравнения можно объединить в одну
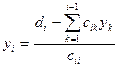 . . | (4.11) |
После того, как все 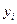 (i = 1, 2,
(i = 1, 2, 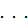 , n) определены по формуле (4.11), их надо подставить в уравнение (4.7), в котором все элементы
, n) определены по формуле (4.11), их надо подставить в уравнение (4.7), в котором все элементы 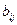 (i, j = 1, 2,
(i, j = 1, 2, 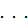 , n) верхней треугольной матрицы В уже известны, так как, повторяем еще раз, что матрица А представлена как произведение двух треугольных.
, n) верхней треугольной матрицы В уже известны, так как, повторяем еще раз, что матрица А представлена как произведение двух треугольных.
В развернутом виде уравнение (4.7) запишется так:
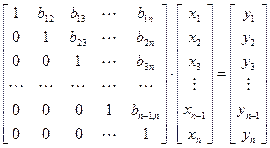 . . | (4.12) |
 Все диагональные элементы матрицы В равны 1. Умножив матрицы в левой части уравнения, получим матрицу-столбец, а учитывая условия равенства двух матриц, будем иметь такую систему уравнений
Все диагональные элементы матрицы В равны 1. Умножив матрицы в левой части уравнения, получим матрицу-столбец, а учитывая условия равенства двух матриц, будем иметь такую систему уравнений
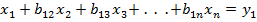 ; ; 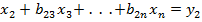 ; ; 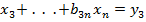 ; ; 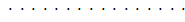 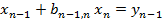 ; ; 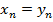 ; ; | (4.13) |
Начиная решение этой системы уравнений с последнего, получим
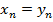
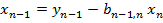 ;
;
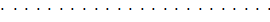
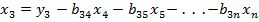 ;
;
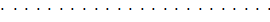
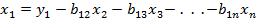 .
.
Общая формула для определения 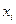 (i = 1, 2,
(i = 1, 2, 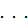 , n) запишется так:
, n) запишется так:
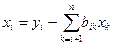 . . | (4.14) |
Для удобства напишем формулы (4.11) и (4.14)
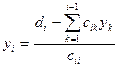
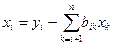
По формуле (7.11) элементы 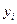 находятся так же, как и элементы
находятся так же, как и элементы 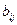 (i < j) верхней треугольной матрицы по формулам (3.21). Ниже приводится так называемая компактная вычислительная схема для применения метода Гаусса решения линейных систем алгебраических уравнений (табл. 1).
(i < j) верхней треугольной матрицы по формулам (3.21). Ниже приводится так называемая компактная вычислительная схема для применения метода Гаусса решения линейных систем алгебраических уравнений (табл. 1).
Таблица 1 указывает компактную схему решения системы линейных алгебраических уравнений. Приведенный аппарат формул для решения системы алгебраических линейных уравнений по способу Гаусса приводит к такому простому правилу:
1. Заготавливаются схемы, аналогичные схеме на следующей странице (табл.1).
2. Вычисления ведутся в такой же последовательности, как и в схеме для формул (3.11) – (3.20) табл. 1 (Практ. зан.З): сначала определяются элементы столбцов, а затем элементы строк, т. е. элементы первого столбца, элементы первой строки; элементы второго столбца, а потом элементы второй строки; элементы третьего столбца, а потом элементы третьей строки и т. д.
3. Чтобы получить элементы, расположенные на главной диагонали или ниже ее, берется соответствующий элемент матрицы А и из него вычитается сумма произведений элементов, расположенных в той же строке и в том же столбце, что и вычисляемый элемент, причем произведения берутся так, что умножается первый элемент в строке на первый элемент в столбце, второй в строке на второй в столбце и т. д.
4. Чтобы получить элемент, стоящий над главной диагональю, поступают так же, как в п. 3, но полученное от вычисления число надо еще разделить на диагональный элемент той же строки, в которой стоит вычисляемый элемент.
5. Искомые неизвестные вычисляются в таком порядке:
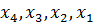
т. е. так называемым «обратным ходом» по формуле (4.14)
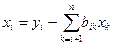
Все вычисления должны быть проконтролированы. Контроль осуществляется так: для него отводится последний столбец и последняя строка вычислительной схемы. Последний столбец делится на две части: верхнюю и нижнюю (см. табл. 1). Элемент верхнего столбца, который мы обозначим через 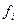 , равен сумме элементов, стоящих с ним в одной и той же строке,
, равен сумме элементов, стоящих с ним в одной и той же строке,
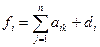 .
.
Элементы же нижнего контрольного, которые мы обозначим через 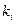 , получаются, как и элементы верхней треугольной матрицы, т. е. по формуле
, получаются, как и элементы верхней треугольной матрицы, т. е. по формуле
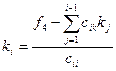 .
.
Таблица 1.
КОМПАКТНАЯ ВЫЧИСЛИТЕЛЬНАЯ СХЕМА ПРИМЕНЕНИЯ СПОСОБА ГАУССА
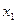 | 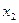 | 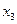 | 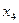 | 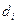 | Контрольный столбец 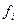 и и 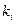 | ||||
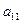 | 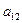 | 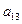 | 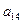 | 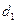 | 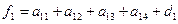 | ||||
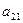 | 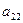 | 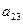 | 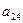 | 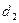 | 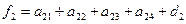 | ||||
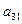 | 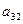 | 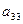 | 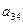 | 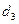 | 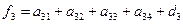 | ||||
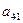 | 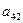 | 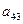 | 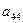 | 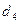 | 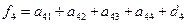 | ||||
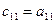 | 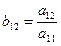 | 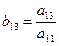 | 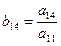 | 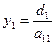 | 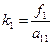 | ||||
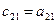 | 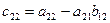 | 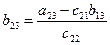 | 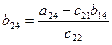 | 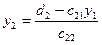 | 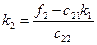 | ||||
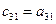 | 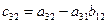 | 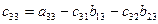 | 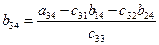 | 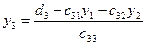 | 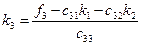 | ||||
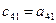 | 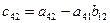 | 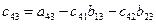 | 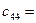 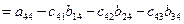 | 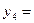 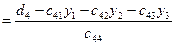 | 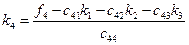 | ||||
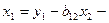 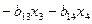 | 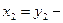 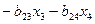 | 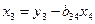 | 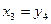 | ||||||
Контроль состоит в том, что элементы контрольного столбца должны быть равны сумме элементов, стоящих в той же строке над главной диагональю. Например, в схеме элементы контрольного столбца должны быть равны:
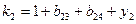 ;
;
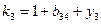 ;
;
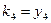 .
.
Контроль должен осуществляться после вычислений каждой строки.
Задача 4.4 Решить по способу Гаусса систему уравнений
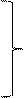
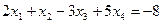 ;
;
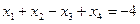 ;
;
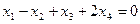 ;
;
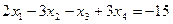 .
.
Решение. Используя указанный аппарат формул (4.11) – (4.14), а также схему, приведенную в табл. 1 на предыдущей странице, располагаем все вычисления, как указано в таблице:
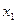 | 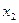 | 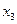 | 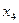 | 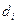 | 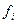 и и 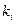 | 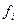 | |||||
| -1 | -8 | ||||||||||
| -1 | -4 | -2 | |||||||||
| -1 | |||||||||||
| -3 | -1 | -15 | -14 | ||||||||
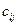 | 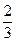 | 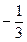 | 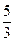 | 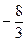 | 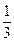 | 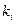 | |||||
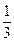 | -2 | -2 | -4 | -7 | |||||||
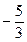 | -2 | 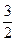 | 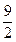 | ||||||||
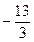 | -9 | 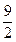 | -2 | -1 | |||||||
| -2 |  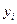 | ||||||||||

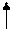
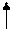

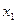
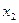
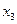
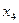
Вычисления проведены в простых дробях для упрощения проверки по ходу решения, следует пользоваться десятичными дробями.
