Циркуляция векторного поля вдоль кривой

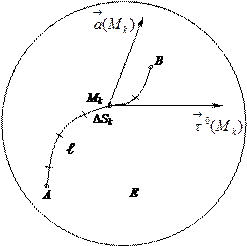Пусть векторное поле 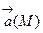определено в пространственной области Е. Выберем в этой области какую-нибудь кривую ℓ. Ориентируем эту кривую, указав на ней положительное направление, для чего установим на ℓ начальную точку А и конечную – В (рис. 1). Пусть 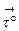– орт касательной в точке М к кривой ℓ, совпадающей по направлению с направлением кривой. Разобьем кривую ℓ любым образом на n "элементарных дуг" длиной DS_k (k=1,2, …,n) в направлении от А к В и в произвольном месте каждой элементарной дуги возьмем по точке M_k .Для k-й элементарной дуги составим произведение

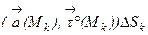(1)

а затем просуммируем все подобные произведения по всем k:

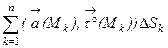(2)

Мы пришли к интегральной сумме первого рода по кривой ℓ. Если функции P, Q, R непрерывны в области Е, а maxDS_k – наибольшая из длин DS_k , то при условии maxDS_k ® 0 сумма (2) стремится к конечному пределу, которым является криволинейный интеграл первого рода от функции 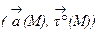по кривой ℓ:

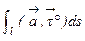. (3)

Вводя в рассмотрение векторный элемент 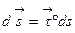линии ℓ с координатами dx, dy, dz, можем представить интеграл (3) в координатной форме:

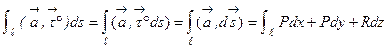. (4)

Особенно большую роль играет в теории поля криволинейный интеграл (4) в случае, когда кривая ℓ, по которой он берется, замкнута, т.е. в случае когда конец В этой кривой совпадает с ее началом А. В этом случае криволинейный интеграл (4) называется циркуляцией векторного поля 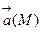по замкнутой кривой ℓ и обозначается символом :

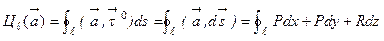. (5)