Дисперсия случайной величины

Математическим ожиданием (ДСВ) X называют сумму произведений всех её возможных значений на их ве­роятности. Для ДСВ X, принимающей значения x₁, x₂, . . ., x_n с вероятностями p₁, p₂,. . ., p_n соответственно, имеем:

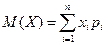
Пусть значения HСB X принадлежат отрезку [а, b]. Математическим ожиданием НCВ X называется величина:

.

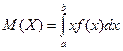Отклонением называют разность между случайной величинойи её математическим ожиданием: X – M(X)

Дисперсией (рассеянием) D(X) ДСВ X называется математическое ожидание квадрата отклонения СВ от ее математического ожидания:

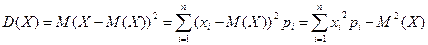
Дисперсией D(X) НСВ X называется величина:

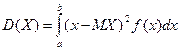
Если возможные значения НСВ X принадлежат всей числовой оси, то пределы интегрирования берутся от -ђ до ђ.

Средним квадратическим отклонением называют корень квадратный из дисперсии:

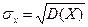
Примеры решения задач

1. Найти вероятность того, что при бросании двух игральных костей выпадет ровно 9 очков.

Решение. Общее число элементарных исходов n=36. Число благоприятных исходов m=4 (3+6, 4+5, 5+4, 6+3). Вероятность:

Р(А) = n/m = 4/36 = 1/9 » 0.111

Ответ: вероятность того, что выпадет 9 очков, равна 0.111.

2. Две зенитные установки выпускают ракеты по самолету. Вероятность попадания первой ракеты 0.8, второй – 0.9. Найти вероятность поражения цели.

Решение. Рассмотрим события: А – попадание первой ракеты, В – попадание второй ракеты. События А и В – совместные. Сумма событий:

Р(А+В) = Р(А) + Р(В) - Р(АВ) = 0.8 + 0.9 - 0.8*0.9 = 0.98

Ответ: вероятность поражения цели 0.98.

3. На склад поступило 3 партии изделий: первая - 2000 штук, вторая - 3000 штук, третья - 1000 штук. Средний процент нестандартных изделий в первой партии 10%, во второй - 5%, в третьей - 15%. Найти вероятность того, что наудачу взятое со склада изделие будет стандартным.

Решение. Всего изделий 2000+3000+1000=6000 штук. Рассмотрим гипотезы: Н₁ – изделие из первой партии, Н₂ – изделие из первой партии, Н₃ – изделие из первой партии. Их вероятности:

Р(Н₁) = 2000/6000=1/3; Р(Н₂) = 3000/6000 = 1/2; Р(Н₃) = 1000/6000 = 1/6

Событие А – наудачу взятое изделие стандартное. Условные вероятности:

Р(А/Н₁) = 0.9; Р(А/Н₂)= 0.95; Р(А/Н₃)= 0.85

Полная вероятность:

Р(А) = Р(Н₁)* Р(А/Н₁) + Р(Н₂)*Р(А/Н₂) + Р(Н₃)*Р(А/Н₃) =

=1/3*0.9 + 1/2*0.95 + 1/6*0.85 = 0.917

Ответ: вероятность того, что наудачу взятое со склада изделие будет стандартным, равна 0.917.

4. В пирамиде 15 снайперских винтовок, из них 5 СС-В и 10 СВД. Вероятность поражения цели из СС-В – 0.9, из СВД – 0.8. Снайпер поразил цель из наудачу взятой винтовки. Что вероятнее, выстрел был произведен из СС-В или из СВД?

Решение. Рассмотрим гипотезы: Н₁ – взята винтовка СС-В, Н₂ – взята винтовка СВД.

Р(Н₁)= 5/15 = 1/3; Р(Н₂)= 10/15 = 2/3

Событие А – цель поражена. Условные вероятности:

Р(А/Н₁)= 0.9; Р(А/Н₂) = 0.8

По формуле Байеса:

Р(Н₁/А)=Р(Н₁)*Р(А/Н₁)/(Р(Н₁)*Р(А/Н₁)+Р(Н₂)*Р(А/Н₂))= 0.36

Р(Н₂/А)=Р(Н₂)*Р(А/Н₂)/(Р(Н₁)*Р(А/Н₁)+Р(Н₂)*Р(А/Н₂))= 0.64

Ответ: вероятность того, что цель была поражена из винтовки СВД, выше, чем из винтовки СС-В.