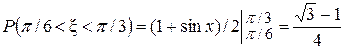Дисперсия случайной величины

Дисперсия непрерывной случайной величины x определяется равенством

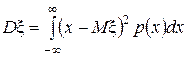(9.7.7)

Дисперсия непрерывной случайной величины имеет те же свойства, что и дисперсия дискретной случайной величины. Величина 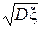называется среднеквадратическим отклонением.

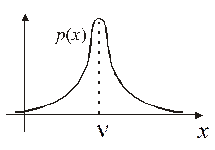
Если график плотности распределения случайной величины x имеет единственный ярко выраженный пик в точке х = n, как на рисунке 4, то это означает, что x принимает с большой вероятностью значения из малого промежутка около х = n (или, иначе, возможные значения x тесно скон­центрированы около числа n). Такая случайная величина имеет относительно малую дисперсию.

Пусть график плотности распре­деления случайной величины x пологий и не имеет выраженного пика, как на рисунке 5. Тогда внутри довольно большой области можно взять различные промежутки одинаковой длины, и вероятности попадания случайной величины в эти промежутки будут отличаться незначи­тельно. В этом случае дисперсия x относительно велика.

Если x – размер детали, выпускаемой автоматическим станком, настроенным на размер n, то график, изображённый на рисунке 4, характерен для случая, когда станок хорошо налажен: отклонения от номинальной величины n встречаются редко или маловероятны. График плотности распределения, изображённый на рисунке 5, свидетельствовал бы о том, что механизм станка расстроен: здесь часто (или с большой вероятностью) встречаются детали с большим отклонением от номинального размера n.

Напомним читателю, что на обоих приведённых рисунках площади фигур, заключённых между горизонтальной координатной осью и графиками плотности распределения, одинаковы и равны единице.

Приведём пример расчёта математического ожидания и дисперсии для случайной величины, равномерно распределённой на промежутке [a; b]. Ранее было получено выражение для плотности распределения такой случайной величины:

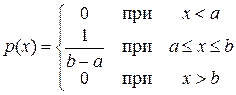
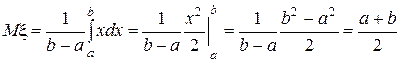
Точка 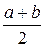лежит в середине промежутка [a; b], и этот результат можно было получить, используя второе из приведённых выше свойств математического ожидания непрерывной случайной величины.

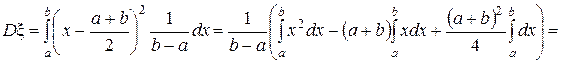
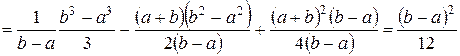(9.7.8)

Отсюда видно, что чем длиннее промежуток, тем больше дисперсия случайной величины, равномерно распределённой на этом промежутке.

Задача 1.

Плотность распределения случайной величины x имеет вид

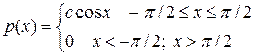
Найти Мx, Dx, F(x), P(p/6 < х < p/3).

Решение.

Сначала определим величину параметра с. По свойству нормировки

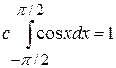
Отсюда следует, что с= 1/2. Математическое ожидание случайной величины равно 0, так как плотность распределения – чётная функция. Дисперсию случайной величины определим по формуле Dx = 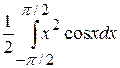. Вычислив определённый интеграл, получаем Dx = p²/4 – 1. Функция F(x) на промежутке (-µ; –p/2) равна нулю, на промежутке (–p/2; p/2) эта функция равна (1 + sinx)/2, на промежутке (p/2; µ) функция равна 1.