Властивості доповнення, різниці та рівності

11) 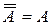;	14) ;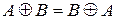
12) 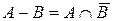;	15) ;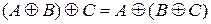
13) 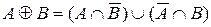;	16) .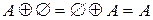

Можна довести, що:

1) Якщо 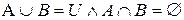, то ;

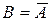2) 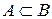тоді і тільки тоді 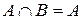тоді і тільки тоді 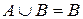тоді і тільки тоді ;

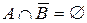3) .

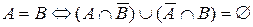Методи доведення тотожностей алгебри множин

Основний метод доведення тотожності в алгебрі множин ґрунтується на застосуванні означення рівності множин і твердження про рівність множин. Такий зручний інструмент, як кола Ейлера може бути використаний для доведення тотожностей алгебри множин тільки після певної формалізації. Ми її не робитимемо, тому використовуватимемо кола Ейлера як ілюстративний інструмент.

Доведемо, наприклад, тотожність 3а) 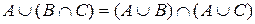, використовуючи твердження про рівність множин. Але спочатку проілюструємо її справжність за допомогою кіл Ейлера. Для цього треба представити на колах Ейлера множину з лівої частини тотожності 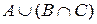і множину з правої частини тотожності 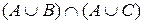і упевнитися в їхній рівності.

Для зображення лівої частини тотожності спочатку закреслюємо штрихом одного напрямку 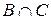, потім штрихом іншого напрямку закреслюємо 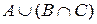. Результатом є область, що закреслена (рис.2.7).

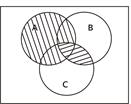
Рис.2.7

Для зображення правої частини тотожності спочатку закреслимо штрихом одного напрямку область 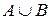, штрихом іншого напрямку область 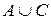. Результатом 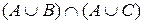буде область подвійного закреслення (рис.2.8).

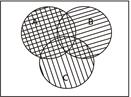
Рис.2.8

Очевидно, що обидві області співпадають (збігаються).

Приклад 2.12. Спочатку доведемо тотожність 3а) 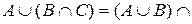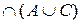, використовуючи твердження про рівність множин.

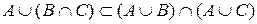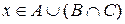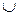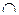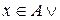
Доведемо, що . Для цього візьмемо будь-яке , тоді за означенням операцій « » і « », 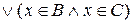. За законом дистрибутивності диз’юнкції відносно кон’юнкції маємо, що 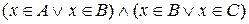, тобт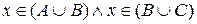о або 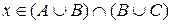, що і було потрібно довести.

Доведемо, що 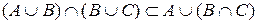. Для цього візьмемо будь-яке 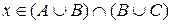. Звідси 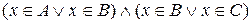або 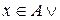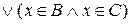, тобто 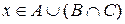, що і було потрібно довести.

Згідно з твердженням про рівність множин 3а) .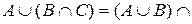

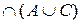Доведемо, що 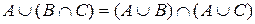за означенням рівності множин. Для цього знову візьмемо будь-яке 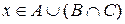, тоді за означенням операцій « 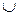» і « 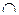», це еквівалентне тому, що 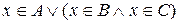. Це в свою чергу за законом дистрибутивності диз’юнкції відносно кон’юнкції еквівалентне тому, що 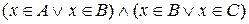, тобт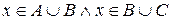о або 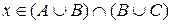. Таким чином ми довели, що

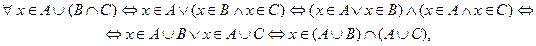
тобто .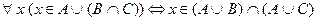

За означенням рівності двох множин це означає, що .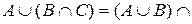

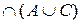Доведемо ту саму тотожність алгебраїчним способом. Нагадаємо, що при цьому ми маємо використовувати основні властивості (тотожності) алгебри множин причому, якщо ми доводитимемо деяку тотожність, то всі інші вважатимемо доведеними.

Адже, треба довести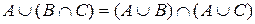

Почнемо з правої частини

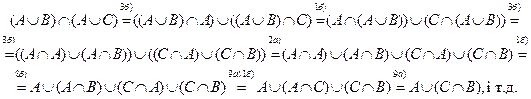
ми отримали ліву частину. Тотожність доведено.

Будь-яка теорема алгебри множин виводиться з тотожностей 2а) і 2б),тобто методом алгебраїчних перетворень.

Приклад 2.13. Доведемо властивість 8а) 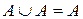, послідовно використовэшргшгщуючи властивості 4б), 5а), 3а), 5б), 4а).

.
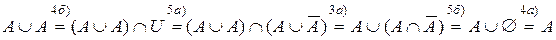