Отображения и функции

Элементы теории функций

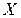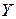Определение 1.Пусть заданы множества и . Отображением множества 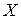в 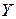или функцией, определенной на множестве 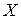и принимающей значения в 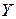, называется соответствие (закон, правило) , по которому каждому элементу 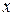из 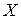сопоставляется один и только один элемент 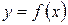из множества .

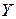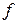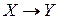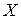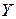Запись : означает, что отображение действует из в . Множество 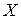называют исходным множеством отображения или областью определения функции , множество 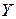- конечным множеством отображения или областью значения функции.

Примеры.

1. «Месяц рождения» может быть правилом, связывающим элементы множества людей 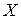с элементами множества месяцев 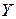. Для каждого элемента 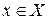существует единственный элемент 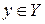, т.к. каждый человек родился в каком-то определенном месяце. В приведенном примере имеет место отображение 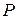множества людей 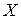в множество месяцев 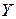, т.е. .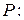

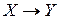2. Рассмотрим два соответствия и 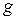, приведенные на рис. 2. Соответствие (рис. 2а) является отображением, т.к. каждому элементу 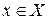сопоставляется единственный элемент 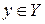. Соответствие 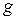(рис. 2б) не является отображением, т.к. элементу 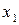(и элементу 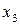) сопоставляется не единственный элемент множества .

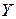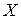
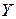
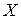
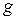
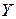
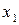
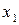
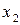
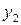
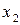
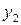
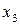
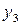
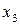
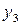
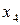
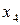
а) б)

Рис. 2

Определение 2.Отображение 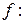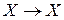, определенное равенством 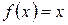называется тождественным и обозначается 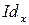, т.е. тождественное отображение 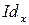: 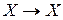оставляет элементы множества 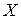на месте.

Определение 3. Отображение 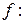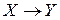называется постоянным, если 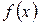для любого элемента 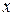из 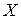является одним и тем же элементом из :

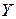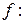
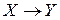, где .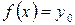

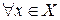Определение 4.Пусть задана функция 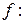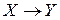. Элемент 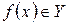, соответствующий элементу 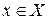при отображении , называется образом элемента 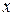или значением функции , соответствующим элементу .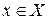

Элемент 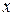обычно называют аргументом функции .