Примеры вычисления двойных интегралов

1. Найти двойной интеграл от функции 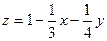по прямоугольной области D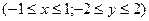

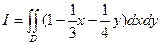
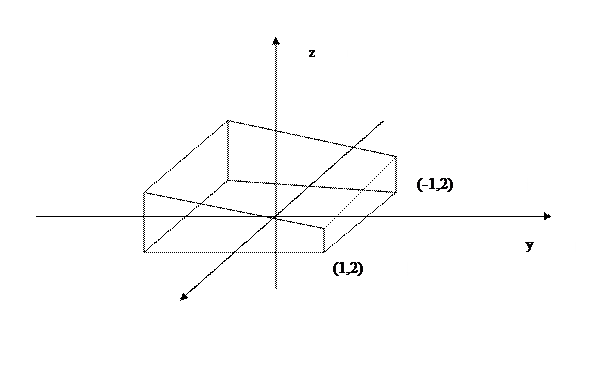
Решение Геометрически I выражает объем четырехугольной призмы, основанием которой служит прямоугольник D, усеченный плоскостью .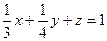

Фигура изображена на следующем рисунке.

х

(1,-2)

Вычислим повторный интеграл сначала по у, затем по х

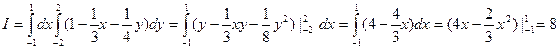
Аналогичный результат получаем, интегрируя сначала по х, затем по у

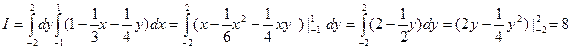
2. Вычислить двойной интеграл 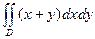по области D, ограниченной линиями y=x и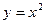

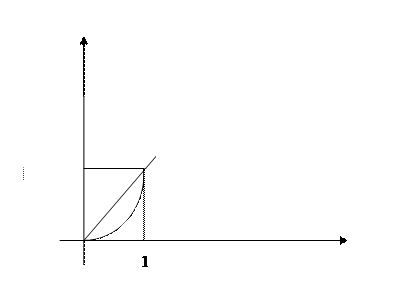
Решение

a) Интегрируем сначала по у, затем по х

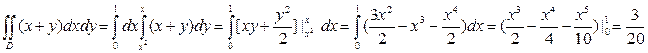
b) Интегрируем сначала по х, затем по у

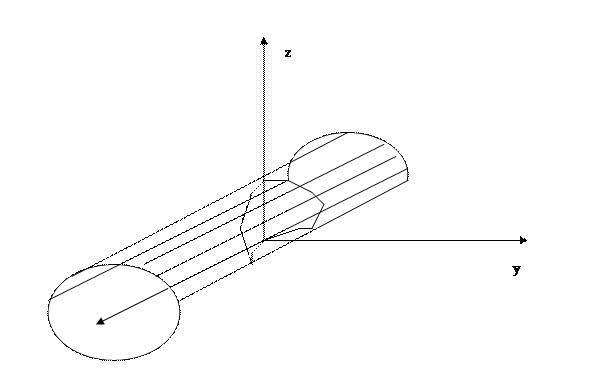
3. Вычислить объем тела, ограниченного цилиндрическими поверхностями 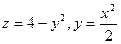и плоскостью z=0

x

Решение

Поверхность, ограничивающая тело сверху имеет уравнение 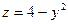. Область интегрирования D получается в результате пересечения параболы 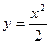с линией пересечения цилиндра 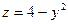и плоскости z=0, то есть с прямой y=2. В виду симметрии тела относительно плоскости OYZ вычисляем половину искомого объема

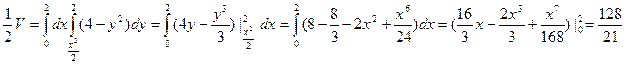
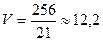
4. Вычислить объем тела, ограниченного поверхностью 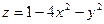и плоскостью OXY.

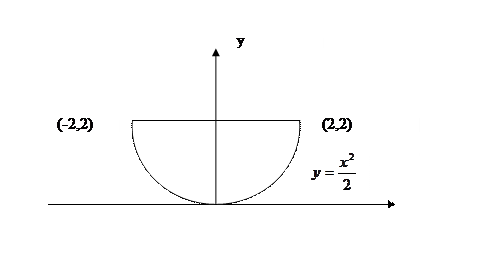
Заданное тело – сегмент эллиптического параболоида, расположенного над плоскостью OXY. Параболоид пересекается с плоскостью OXY по эллипсу 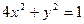. Следовательно, необходимо вычислить объем тела, имеющего своим основанием внутреннюю часть указанного эллипса и ограниченного параболоидом. В силу симметрии относительно плоскостей OXZ и OYZ можно вычислить объем четвертой его части, заключенной в первом октанте. Область интегрирования 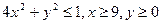(см. рисунок)

Интегрируем сначала по у, затем по х

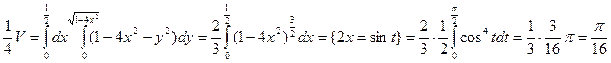
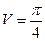
Замена переменных в двойном интеграле

Полярные координаты

При вычислении определенных интегралов важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий имеет место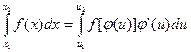

Обычно функция 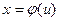монотонна; тогда она осуществляет взаимнооднозначное соответствие между точками интервала 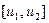изменения переменной u и точками интервала 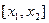изменения переменной х.

Заменяя 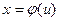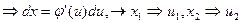. Правило замены переменной в двойном интеграле достаточно сложное. Приведем формулу замены.

При переходе в двойном интеграле от переменных x,y к новым переменным u,v: x=x(u,v), y=y(u,v) (*) формула замены такова

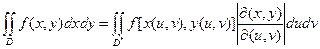(**), где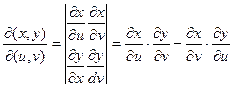

Есть функциональный определитель Якоби (Якобиан) составленный из частных производных функций (*), то есть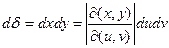

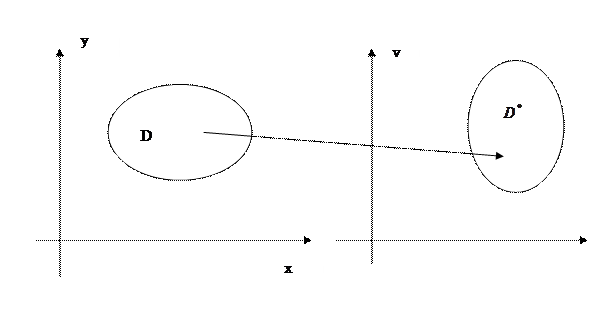
Старая область интегрирования D заменяется на новую область 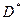по переменным u,v. Новое выражение для 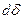называется элементом площади в координатах u,v.

При удачной замене переменных преобразованный интеграл может оказаться проще чем исходный, например, пределы интегрирования могут оказаться постоянными.

u