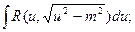Определение: Плоскость, проходящая через касательную и главную нормаль к кривой в точке А называется соприкасающейся плоскостью
Определение: Нормаль к кривой, перпендикулярная к соприкасающейся плоскости, называется бинормалью.Ее единичный вектор- 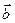 .
.
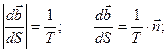
Величина 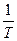 называется кручением кривой.
называется кручением кривой.
Ниже рассмотрим несколько примеров исследования методами дифференциального исчисления различных типов функций.
Пример: Методами дифференциального исчисления исследовать функцию 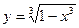 и построить ее график.
и построить ее график.
1. Областью определения данной функции являются все действительные числа (-¥; ¥).
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;
с осью Ох: y = 0; x = 1;
4. Точки разрыва и асимптоты: Вертикальных асимптот нет.
Наклонные асимптоты: общее уравнение y = kx + b;
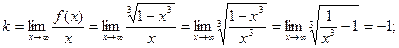
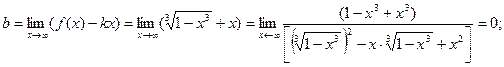
Итого: у = -х – наклонная асимптота.
5. Возрастание и убывание функции, точки экстремума.
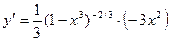 . Видно, что у¢< 0 при любом х ¹ 0, следовательно, функция убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
. Видно, что у¢< 0 при любом х ¹ 0, следовательно, функция убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
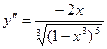 y¢¢ = 0 при х =0 и y¢¢ = ¥ при х = 1.
y¢¢ = 0 при х =0 и y¢¢ = ¥ при х = 1.
Точки (0,1) и (1,0) являются точками перегиба, т.к. y¢¢(1-h) < 0; y¢¢(1+h) >0; y¢¢(-h) > 0; y¢¢(h) < 0 для любого h > 0.
6. Построим график функции.
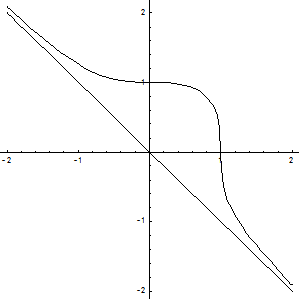
Пример: Исследовать функцию 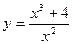 и построить ее график.
и построить ее график.
1. Областью определения функции являются все значения х, кроме х = 0.
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Ох: y = 0; x = 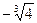
с осью Оу: x = 0; y – не существует.
4. Точка х = 0 является точкой разрыва 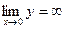 , следовательно, прямая х = 0 является вертикальной асимптотой.
, следовательно, прямая х = 0 является вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.
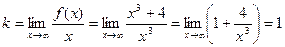
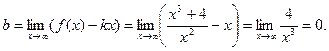
Наклонная асимптота у = х.
5. Находим точки экстремума функции.
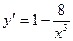 ; y¢ = 0 при х = 2, у¢ = ¥ при х = 0.
; y¢ = 0 при х = 2, у¢ = ¥ при х = 0.
y¢ > 0 при х Î (-¥, 0) – функция возрастает,
y¢ < 0 при х Î (0, 2) – функция убывает,
у¢ > 0 при х Î (2, ¥) – функция возрастает.
Таким образом, точка (2, 3) является точкой минимума.
Для определения характера выпуклости/вогнутости функции находим вторую производную.
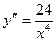 > 0 при любом х ¹ 0, следовательно, функция, вогнутая на всей области определения.
> 0 при любом х ¹ 0, следовательно, функция, вогнутая на всей области определения.
6. Построим график функции.
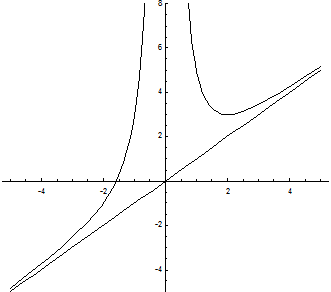
Пример: Исследовать функцию 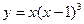 и построить ее график.
и построить ее график.
1. Областью определения данной функции является промежуток х Î (-¥, ¥).
2. В смысле четности и нечетности функция является функцией общего вида.
3. Точки пересечения с осями координат: с осью Оу: x = 0, y = 0;
с осью Ох: y = 0, x = 0, x = 1.
4. Асимптоты кривой.
Вертикальных асимптот нет.
Попробуем найти наклонные асимптоты в виде y = kx + b.
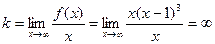 - наклонных асимптот не существует.
- наклонных асимптот не существует.
5. Находим точки экстремума.
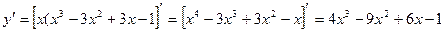
Для нахождения критических точек следует решить уравнение 4х3 – 9х2 +6х –1 = 0.
Для этого разложим данный многочлен третьей степени на множители.
Подбором можно определить, что одним из корней этого уравнения является число
х = 1. Тогда:
 4x3 – 9x2 + 6x – 1 x - 1
4x3 – 9x2 + 6x – 1 x - 1
` 4x3 – 4x2 4x2 – 5x + 1
- 5x2 + 6x
` - 5x2 + 5x
x - 1
` x - 1
Тогда можно записать (х – 1)(4х2 – 5х + 1) = 0. Окончательно получаем две критические точки: x = 1 и x = ¼.
Примечание. Операции деления многочленов можно было избежать, если при нахождении производной воспользоваться формулой производной произведения:
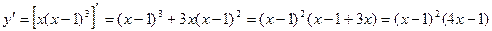
Найдем вторую производную функции: 12x2 – 18x + 6. Приравнивая к нулю, находим:
x = 1, x = ½.
Систематизируем полученную информацию в таблице:
| (-¥ ; ¼) | 1/4 | ( ¼ ; ½) | 1/2 | ( ½ ; 1 ) | (1 ; ¥) | ||
| f¢¢(x) | + | + | + | - | + | ||
| f¢(x) | - | + | + | + | + | ||
| f(x) | убывает вып.вниз | min | возрастает вып.вниз | перегиб | возрастает вып.вверх | перегиб | возрастает вып. вниз |
6. Построим график функции.
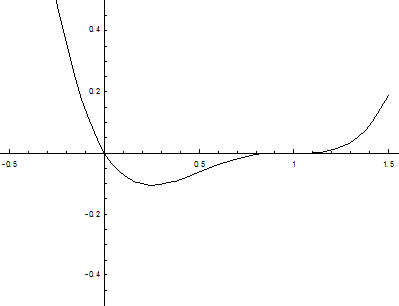
Интегральное исчисление.
Первообразная функция.
Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Определение: Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 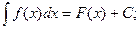
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 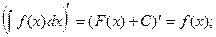
2. 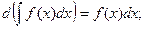
3. 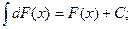
4. 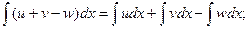 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
6. 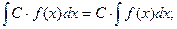
Пример: 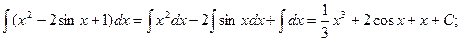
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
| Интеграл | Значение | Интеграл | Значение | ||
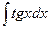 | -ln½cosx½+C | 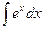 | ex + C | ||
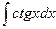 | ln½sinx½+ C | 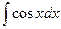 | sinx + C | ||
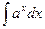 | 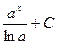 | 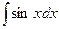 | -cosx + C | ||
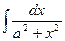 | 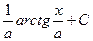 | 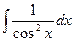 | tgx + C | ||
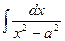 | 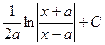 | 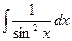 | -ctgx + C | ||
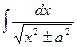 | ln 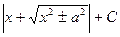 | 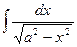 | arcsin 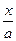 + C + C | ||
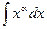 | 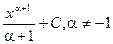 | 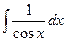 | 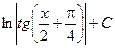 | ||
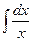 | 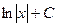 | 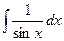 | 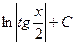 |
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 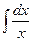 . На основе известной формулы дифференцирования
. На основе известной формулы дифференцирования 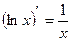 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 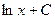 , где С – некоторое постоянное число. Однако, с другой стороны
, где С – некоторое постоянное число. Однако, с другой стороны 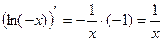 . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод:
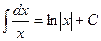
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 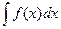 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
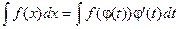
Доказательство: Продифференцируем предлагаемое равенство:
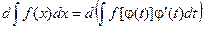
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти неопределенный интеграл 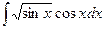 .
.
Сделаем замену t = sinx, dt = cosxdt.
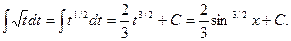
Пример. 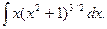
Замена 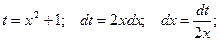 Получаем:
Получаем:
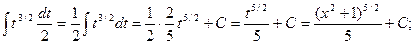
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 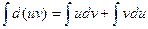 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
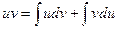 или
или 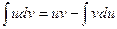 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. 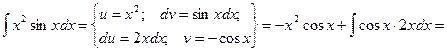
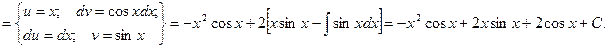
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример. 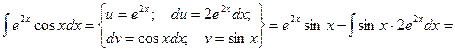
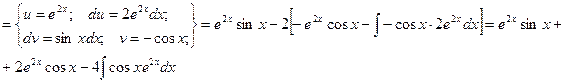
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
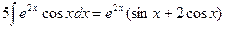
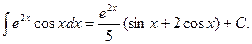
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
Пример.
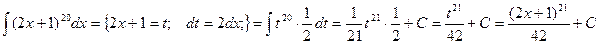
Пример.
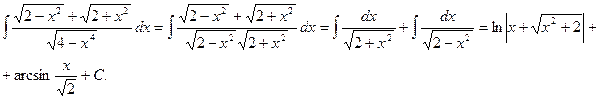
Пример.
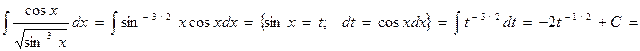
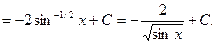
Пример.
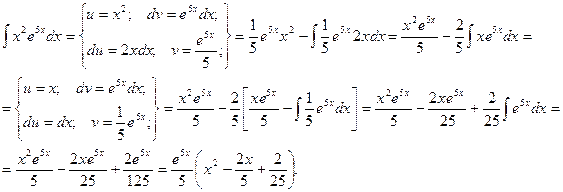
Пример.
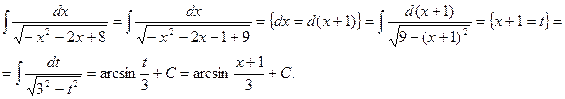
Пример.
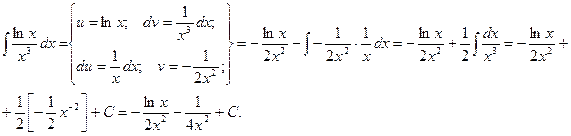
Пример.
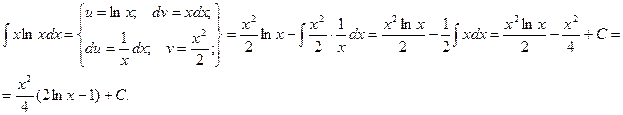
Пример.
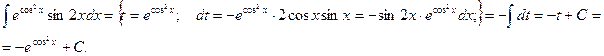
Пример.
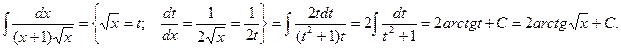
Пример.
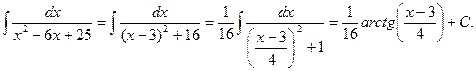
Интегрирование элементарных дробей.
Определение: Элементарныминазываются дроби следующих четырех типов:
I. 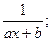 III.
III. 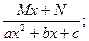
II. 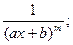 IV.
IV. 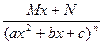
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 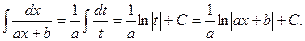
II. 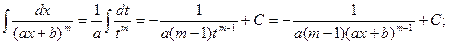
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
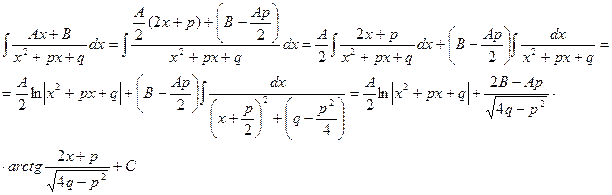
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
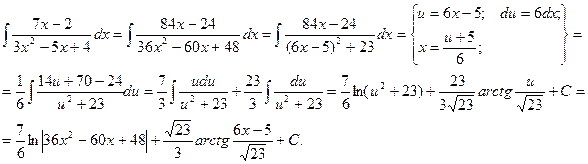
Вообще говоря, если у трехчлена ax2 + bx + c выражение b2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.
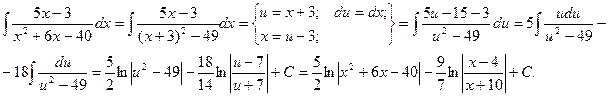
Пример.
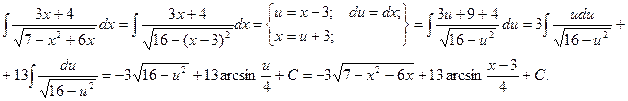
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида 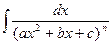 можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 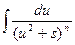 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
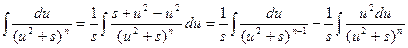 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 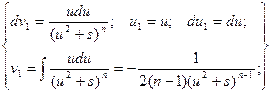
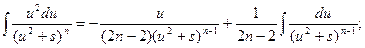
Для исходного интеграла получаем:
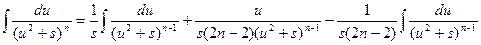
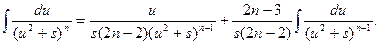
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 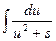 .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
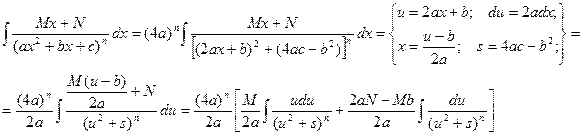
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному 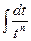 , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример:
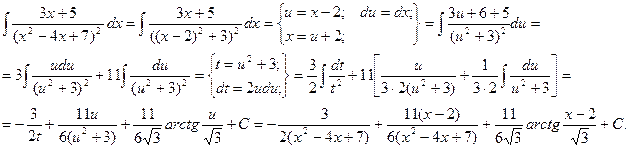
Интегрирование рациональных функций.
Интегрирование рациональных дробей.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если 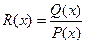 - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
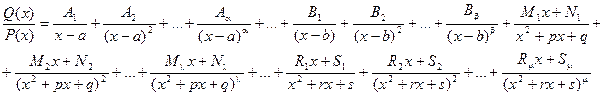
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
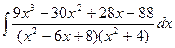
Т.к. ( 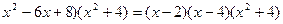 , то
, то
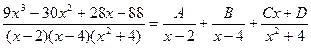
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
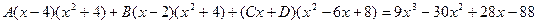
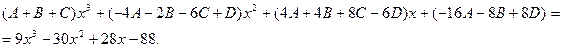
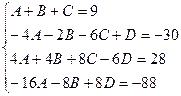
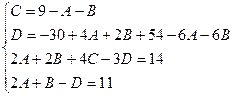
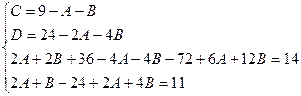
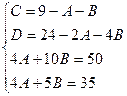
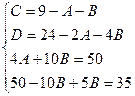
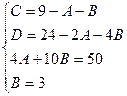
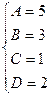
Итого:
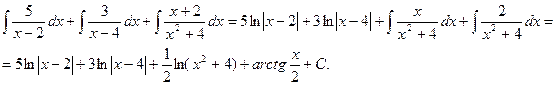
Пример.
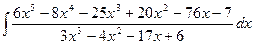
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
 6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
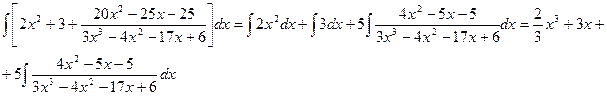
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
 3x3 – 4x2 – 17x + 6 x - 3
3x3 – 4x2 – 17x + 6 x - 3
3x3 – 9x2 3x2 + 5x - 2
5x2 – 17x
5x2 – 15x
- 2x + 6
-2x + 6
Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:
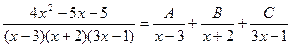
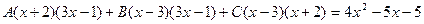
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
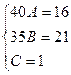
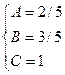
Окончательно получаем:
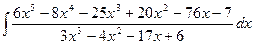 =
= 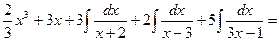
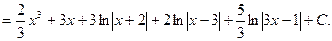
Пример.
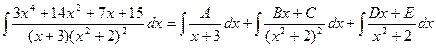
Найдем неопределенные коэффициенты:
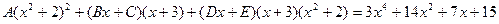
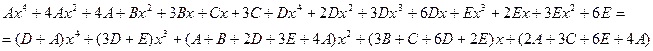
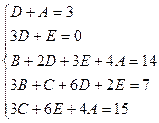
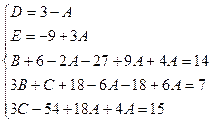
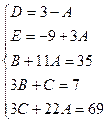
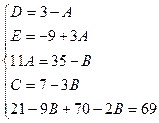
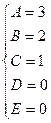
Тогда значение заданного интеграла:
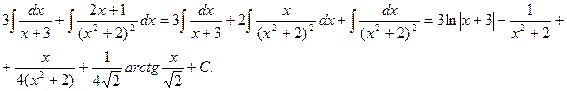
Интегрирование некоторых тригонометрических
функций.
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл вида 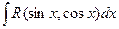 .
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки 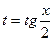 . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
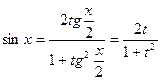 ,
, 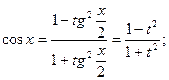
Тогда 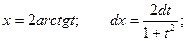
Таким образом: 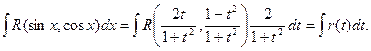
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Пример.
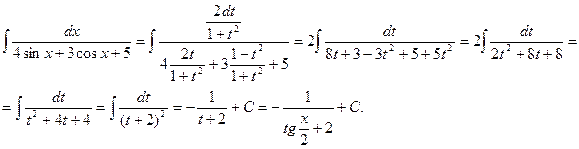
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
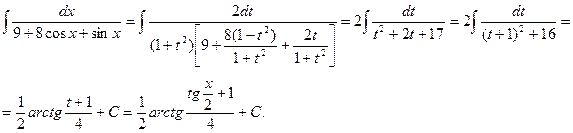
Интеграл вида 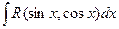 если
если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
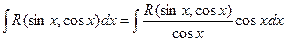
Функция 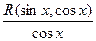 может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
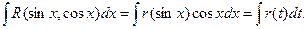
Пример.
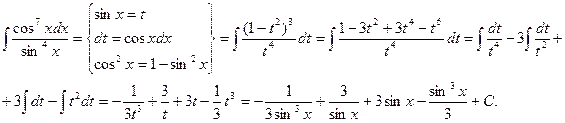
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида 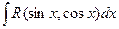 если
если
функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда 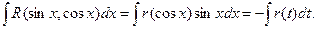
Пример.
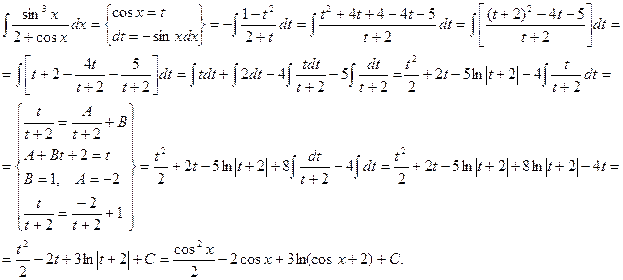
Интеграл вида 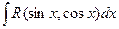
функция R четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда 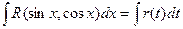
Пример.
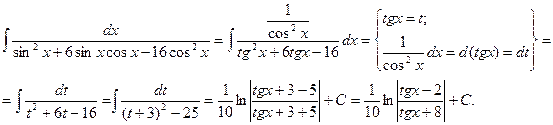
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
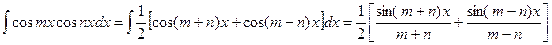
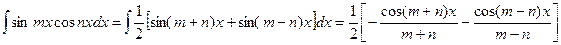
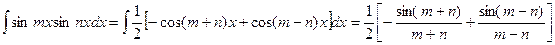
Пример.
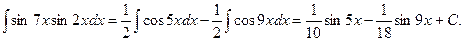
Пример.
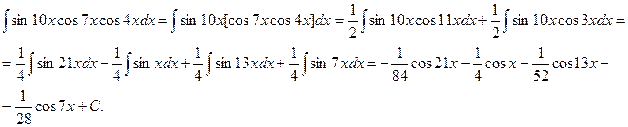
Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.
Пример.
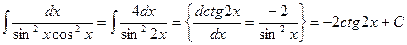
Пример.
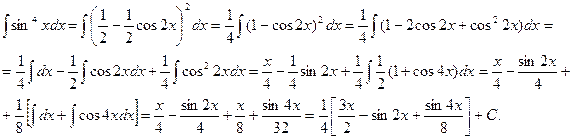
Иногда применяются некоторые нестандартные приемы.
Пример.
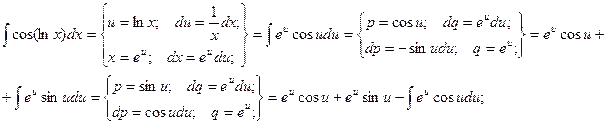
Итого 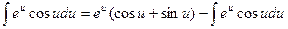
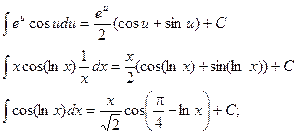
Интегрирование некоторых иррациональных функций.
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл вида 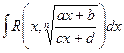 где n- натуральное число.
где n- натуральное число.
С помощью подстановки 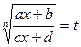 функция рационализируется.
функция рационализируется.
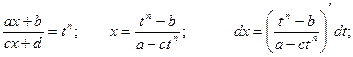
Тогда 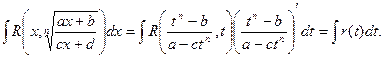
Пример.
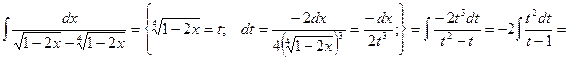
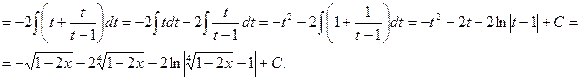
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
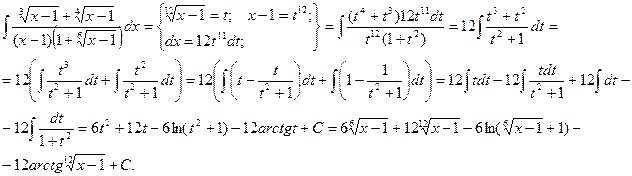
Интегрирование биноминальных дифференциалов.
Определение: Биноминальным дифференциаломназывается выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
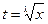 , где l - общий знаменатель m и n.
, где l - общий знаменатель m и n.
2) Если 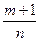 - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой
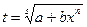 , где s – знаменатель числа р.
, где s – знаменатель числа р.
3) Если 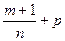 - целое число, то используется подстановка
- целое число, то используется подстановка 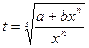 , где s – знаменатель числа р.
, где s – знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы вида 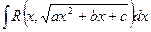 .
.
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
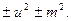
Таким образом, интеграл приводится к одному из трех типов:
1) 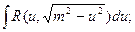
2) 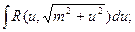
3)