Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью
Прямая и плоскость пересекаются если 
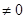 т.е. не параллельны ; перпендикулярны, когда
т.е. не параллельны ; перпендикулярны, когда 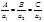 , параллельны, если
, параллельны, если 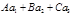 =0, Ах0+Ву0+Сz0+D
=0, Ах0+Ву0+Сz0+D 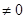 - означает что векторы n и а перпендикулярны,т.е прям .и плоскость параллельны, но точка М0 (х0,у0,z0) прямой не принадлежит плоскости.; совпадают когда
- означает что векторы n и а перпендикулярны,т.е прям .и плоскость параллельны, но точка М0 (х0,у0,z0) прямой не принадлежит плоскости.; совпадают когда 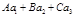 =0, Ах0+Ву0+Сz0+D=0 – прямая лежит в плоскости.
=0, Ах0+Ву0+Сz0+D=0 – прямая лежит в плоскости.
Синус угла между прямой х=х0 +а1t , y=y0+a2t , z=z0+a3t и плоскостью Ах+Ву+Сz+D=0 определяется формулой 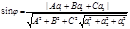
21вопрос Общее уравнение поверхности второго порядка. Поверхности вращения. Конические поверхности. Цилиндрические поверхности.
Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:
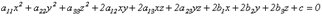 уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии lвокруг неподвижной прямой i - оси вращения поверхности
Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса
Если найти собственные числа и нормированные собственные векторы матрицы квадратичнойформы 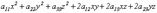 и перейти к системе координат, определяемой базисом из ортонормированных собственных векторов, уравнение (12.1) можно привести к одному из следующих видов:
и перейти к системе координат, определяемой базисом из ортонормированных собственных векторов, уравнение (12.1) можно привести к одному из следующих видов:
Эллипсоид
Каноническое уравнение эллипсоида имеет вид 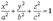 .
.
Из этого уравнения следует | x | < a, | у | < b, | z | < c, то есть эллипсоид заключён в прямоугольный параллелепипед со сторонами 2·а, 2·b, 2·c. Координатные плоскости являются плоскостями симметрии.
Однополостный гиперболоид
Каноническое уравнение однополостного гиперболоида имеет вид 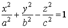 .
.
Координатные плоскости являются плоскостями симметрии, так как при замене х на − х, у на − у, z на − z уравнение не меняется.
Двуполостный гиперболоид
Каноническое уравнение двуполостного гиперболоида имеет вид
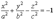 .
.
Эллиптический параболоид
Каноническое уравнение эллиптического параболоида имеет вид
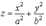 .
.
Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид
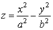 .
.
Эллиптический конус
Каноническое уравнение эллиптического конуса имеет вид
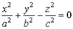 .
.
Координатные плоскости являются плоскостями симметрии: при замене х на - х, у на - у, z на - z уравнение не меняется.
Цилиндрической поверхностью называется поверхность, полученная движением прямой (образующей), перемещающейся параллельно некоторому вектору и пересекающей во время движения фиксированную линию (направляющую).
В результате получим уравнение искомой цилиндрической поверхности F(x, y, z) = 0. Здесь уравнение направляющей определяется системой уравнений

Уравнение 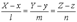 определяет уравнение образующей.
определяет уравнение образующей.
Эллиптический цилиндр
Уравнение эллиптического цилиндра имеет вид
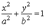 .
.
Гиперболический цилиндр
Уравнение гиперболического цилиндра имеет вид
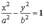 .
.
Параболический цилиндр
Уравнение гиперболического цилиндра имеет вид y2 = 2 p x.
ВОПРОС Эллипсоид.
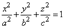
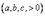 (7)
(7)
При 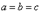 эллипсоид (7) обращается в сферу радиуса
эллипсоид (7) обращается в сферу радиуса  с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии
с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии  .
.
Величины  называются полуосями эллипсоида.
называются полуосями эллипсоида.
Если в уравнении (7) заменить (одновременно или порознь)  на
на  ,
,  на
на 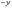 ,
,  на
на 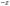 , то оно не изменится, — это показывает, что эллипсоид (7) есть поверхность, симметричная относительно координатных плоскостей
, то оно не изменится, — это показывает, что эллипсоид (7) есть поверхность, симметричная относительно координатных плоскостей  ,
,  ,
,  и начала координат. Поэтому достаточно изучить уравнение (7) в первом октанте (системы координат), т. е. для
и начала координат. Поэтому достаточно изучить уравнение (7) в первом октанте (системы координат), т. е. для  ,
, 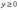 ,
,  . Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
. Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
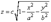 ,
, 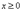 ,
, 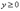 ,
, 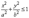 .
.
Для определенности будем считать, что  . Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса
. Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса  с центром в начале координат: для координат любой точки эллипсоида
с центром в начале координат: для координат любой точки эллипсоида  имеет место неравенство
имеет место неравенство
 .
.
Чтобы составить более точное представление об эллипсоиде, произведем сечения плоскостями, параллельными координатным плоскостям. Например, пересекая эллипсоид плоскостями 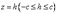 , получим в сечении эллипсы
, получим в сечении эллипсы
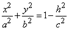
с полуосями 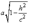 ,
, 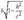 .
.
Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью  . Аналогичная картина будет при сечении плоскостями
. Аналогичная картина будет при сечении плоскостями 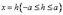 ,
, 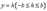 .
.
Точки 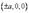 ,
,  ,
,  лежат на эллипсоиде (7) и называются его вершинами.
лежат на эллипсоиде (7) и называются его вершинами.
Если какие-либо две полуоси равны между собой, то эллипсоид (7) будет эллипсоидом вращения, т. е. получается от вращения эллипса относительно соответствующей оси координат.
23ВОПРОС Гиперболоиды.
Однополостной гиперболоид – поверхность, определяемая в некоторой прямоугольной системе координат уравнением 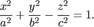 (1)
(1)
Двуполостной гиперболоид – поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением 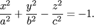 (2) В уравнениях a, b, с — положительные параметры, характеризующие гиперболоиды, причем a ≥ b.
(2) В уравнениях a, b, с — положительные параметры, характеризующие гиперболоиды, причем a ≥ b.
Начало координат называют центром гиперболоида. Вершина – точка пересечения гиперболоида с координатными осям. Это четыре точки однополостного гиперболоида (4.48) и две точки двуполостного гиперболоида (4.49). Три отрезка координатных осей, соединяющих вершины гиперболоидов, называются осями гиперболоидов. Оси гиперболоидов, принадлежащие координатным осям , называются поперечными осями гиперболоидов, а ось, принадлежащая оси аппликат , — продольной осью гиперболоидов. Числа , равные половинам длин осей, называются полуосями гиперболоидов. Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.
Уравнение (1) наз-ся каноническим уравнением однополосного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (1) то оси Ох, Оу и Oz наз-ся его главными осями.
Установим вид поверхности (1). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
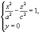 и
и 
из которых следует, что в сечениях получаются гиперболы. Теперь рассм-м сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями  или
или 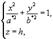 из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями 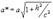 и
и 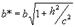 ,
,
достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании 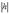 величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно.
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида. Если a=b,то гиперболоид может быть получен вращением гиперболы с полуосями а и с вокруг мнимой оси 2с.
Параболоиды.
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.
Канонические уравнения параболоида в декартовых координатах:
Z=ax2 +by2
если a и b одного знака, то параболоид называется эллиптическим.
если a и b разного знака, то параболоид называется гиперболическим.
если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Эллиптический параболоид
Эллиптический параболоид при a=b=1
Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида
Z=  +
+ 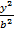 Где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.
Где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.
Если a=b то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы.
Гиперболический параболоид
Гиперболический параболоид при a=−b=1
Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида
Z=  -
- 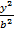 =(
=(  +
+  ) (
) (  -
-  )
)
Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью.
Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной.
Линейное векторное пространство. Подпространство. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов. Преобразование координат вектора при замене базиса.
Линейным действительным пространством или векторным действительным пространством наз. множество V элементов x,y,z…, для которых определены операции сложения элементов и умножения элемента на действительное число,удовлетворяющее след. аксиомам:
1. х+у=х+у,
2.(х+у)+z=x+(y+z),
3. существует элемент 0 такой, что x+0=x
4. для каждого x существует элемент -x, такой что x+(-x)=0
5. 1*x=x
6. a*(b*x)=(a*b)*x
7. (a+b)x=ax+bx
8. a(x+y)=ax+ay
Множество W Ì V наз.подпространством линейного пространства V,если выполняются след. условия:
1.в множестве W определены те же операции,что и в множестве V
2.если х,у ∈ W, то х+у ∈ W
3.если х ∈ W, то αх ∈ W.
Система векторов наз. линейно независимой,если линейная комбинация этих векторов λ1а1 + λ2а2 +…+ λnаn =0 тогда и только тогда ,когда все λ =0
Система векторов наз. линейно зависимой,если существует такая линейная комбинация этих векторов =0,где не все λ =0
Базисом системы векторов наз. такая подсистема в которой все вектора линейно независимы и любой др. вектор явл. линейной комбинацией векторов этой подсистемы.
Число n наз. размерностью линейного пространства V, если выполняются следующие условия:1. в V существует n линейно независимых векторов.2. любая система n+1 векторов из V линейно зависима.
Координатами вектора х в базисе е1,е2,…,еn наз. коэффициенты α1, α2,… αn в разложении этого вектора по данному базису,т.е. в формуле
х=α1е1 + α2е2+…+ αnen
Если система векторов e1, ..., en n-мерного линейного пространства Ln образует базис в Ln, то любой вектор x из Lnможет быть представлен в виде
x = С1·e1+ С2·e2+ ...+ Сn· en.
Выражение x = С1·e1+ С2·e2+ ...+ Сn· en называется разложением вектора по базису e1, ..., en, а числа С1, С2, ..., Сn называются координатами вектора x в базисе e1, ..., en.
Координаты вектора принято обозначать тем же символом, что и сам вектор:
x = x1·e1+ x2·e2+ ...+ xn· en.
Взаимно однозначное соответствие x = x1·e1+ x2·e2+ ...+ xn· en ⇐⇒x = (x1, x2, ..., xn)— изоморфизм Ln и Rn.
