Конструктивных моделей теория

- один из разделов математики, возникший на границе моделей теории, алгебры и теории рекурсивных функций и связанный с изучением вопросов эффективности в моделях и алгебрах.

Статья А. И. Мальцева "Конструктивные алгебры" [1] явилась первой обзорной работой по конструктивным моделям, в к-рой были выработаны и систематизированы основные понятия и намечены дальнейшие пути развития этой теории. Большую роль в становлении и развитии этого раздела математики сыграли работы Ю. Л. Ершова и его учеников, в которых был решен ряд основных проблем, выработаны новые понятия и определены новые направления в исследовании конструктивных моделей (см. [2]).

Ниже сформулированы основные понятия и результаты К. м. т. Все рассмотрения обычно ведутся в некоторой фиксированной сигнатуре

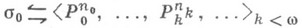
такой, что функция 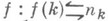общерекурсивна. Если рассматриваются алгебраич. системы, то в сигнатуре могут быть и функциональные символы. Используется также сигнатура

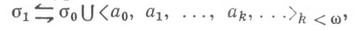
к-рая получается присоединением к s₀ счетного числа символов для констант. Всегда предполагается, что п ₀=2 и предикат 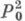на любой модели определен как равенство. Пусть L_i,i=0,1,- совокупность всех формул узкого исчисления предикатов с равенством 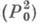сигнатуры s_i, i=0,1, и g- некоторая фиксированная геделевская нумерация (см. [3]) множества 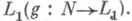Подмножество 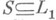наз. разрешимым, если множество g^-1(S)рекурсивно. Нумерованной моделью (сигнатуры s₀) наз. 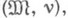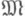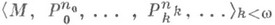пара где = - модель сигнатуры s₀, a v - нумерация основного множества М модели 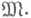Нумерованная модель 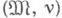наз. конструктивной моделью, если множество рекурсивно.

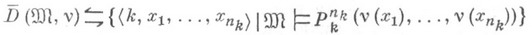
По каждой нумерованной модели 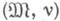можно каноническим образом построить некоторое s₁-oбогащение 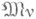модели 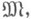т. е. модель сигнатуры s₁, основное множество к-рой есть основное множество модели 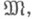предикаты из s₀ в 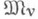совпадают с соответствующими предикатами 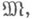а константы определены следующим образом: в качестве значения а _k, k<w, полагают элемент Пусть 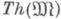- элементарная теория модели 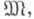т. е. множество всех замкнутых формул сигнатуры s₀, истинных на модели 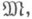а 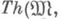v)- элементарная теория нумерованной модели 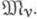Нумерованная модель 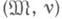наз. сильно конструктивной, если теория 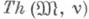разрешима.

Непосредственно из определения видно, что сильно конструктивная модель конструктивна.

Одной из основных проблем К. м. т. является проблема существования конструктивных моделей с различными элементарными свойствами, т. е. свойствами, записываемыми на языке узкого исчисления предикатов. В этом направлении получен (к 1978) ряд интересных и важных теорем. Существование широкого класса сильно конструктивных моделей дает следующая теорема: если - разрешимая теория, то существует такая последовательность сильно конструктивных моделей

что: 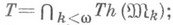множество {{х, y)|g{y) 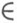Th( 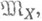v_x)} является рекурсивным. Было замечено, что существуют формулы, не имеющие конструктивных моделей. Следующие две теоремы дают некоторые достаточные условия существования конструктивных моделей у теорий с рекурсивно перечислимым множеством аксиом.

Если Т- рекурсивно перечислимая 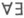-теория, имеющая модель 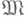с рекурсивно перечислимой 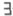-теорией, то теория Т имеет конструктивную модель.

Теория Т-конечной сигнатуры s= 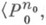. . ., 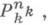с ₀, . .. , c_l )наз. 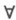-конечной, если универсальная теория любого расширения (той же сигнатуры) конечно аксиоматизируема (универсальными предложениями). Теория Т наз. сильно 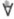-конечной, если для любого конечного множества константных символов теория Т*, определенная теорией Т в языке сигнатуры 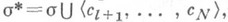является 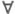-конечной.

Если теория Т сильно 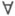-конечна, а Т'- рекурсивно перечислимое расширение Т, то Т' имеет конструктивную модель.

Другой круг исследуемых вопросов связан с проблемой существования для заданной модели 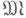нумерации v такой, чтобы пара 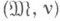стала (сильно) конструктивной моделью. Модель, для к-рой существует такая нумерация, наз. (сильно) конструктивизируемой, а соответствующая нумерация (сильной) конструктивизацией. Для решения ряда вопросов, связанных с конструктивизируемостью моделей, оказывается полезной теорема Ершова о ядре, применение которой к конкретным алгебраическим системам позволяет решить ряд естественных вопросов. В частности, установлено: 1) для любой конструктивной локально нильпотентной группы без кручения существует конструктивное пополнение; 2) если (F, v) - конструктивное поле, F₀- алгебраическое расширение поля F, то v продолжается до конструктивизации поля F₀ тогда и только тогда, когда семейство конечных множеств многочленов над F от счетного числа переменных, имеющих корень в F, рекурсивно перечислимо.

Большой класс конструктивизируемых моделей дает следующая теорема: любая счетная модель 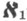-категоричной разрешимой теории сильно конструктивизируема. Интересным является вопрос о (сильной) конструктивизируемости специальных моделей полных теории, в частности простых и универсальных. Найдены необходимые и достаточные условия (сильной) конструктивизируемости простой (и счетной насыщенной) модели полной теории; построены примеры полных теорий с неконструктивизируемыми простой и универсальной моделями. Доказано, что простая модель полной разрешимой теории, имеющей сильно конструктивизируемую универсальную модель или конечное число попарно неизоморфных счетных моделей, всегда сильно конструктивизируема.

Изучался вопрос о числе неэквивалентных конструктивизаций для данной модели. Две конструктивизации v и m. модели 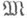наз. (рекурсивно) эквивалентными, если существуют изоморфизм j(j= 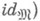и рекурсивная функция f такие, что jv=mf. Модель наз. (рекурсивно устойчивой) автоустойчивой, если любые две ее конструктивизации (рекурсивно) эквивалентны.

Для широкого класса алгебраических систем показано, что существует либо только одна (с точностью до эквивалентности), либо счетное число неэквивалентных конструктивизаций [4], [5]. Полностью решен вопрос о числе неэквивалентных конструктивизаций и описаны автоустойчивые модели для полей, булевых алгебр и абелевых групп без кручения. А также показано, что вопросы автоустойчивости связаны с изучением вычислимости классов конструктивных моделей.

Литература:

[1] Мальцев А. И., "Успехи матем. наук", 1961, т. 16, № 3, с. 3-60;

[2] Ершов Ю. Л., Теория нумераций ч. 3 - Конструктивные модели, Новосиб., 1974;

[3] Ершов Ю. Л. и др., "Успехи матем. наук", 1965, т. 20, № 4, с. 37-108;

[4] Гончаров С. С, "Алгебра и логика", 1975, т. 14 № 6,с. 647-80;

[5] Нуртазин А. Т., там же, 1974, т. 13, № 3, с. 311-23;

[6] Соbham А., в кн.: Summaries of talks presented at the Summer Institute for Symbolic Logic Cornell University 1957, Wash., 1960, p. 391-95;