Оценка уравнения регрессии и построение доверительных интервалов для коэффициентов регрессии
Для построения уравнения регрессии в Statistica 6.0в меню «Статистика» выбирают функцию– «Множественная регрессия», после чего активизируется окно выбранного анализа и предлагается сделать выбор зависимой и независимой переменных (рис. 7).
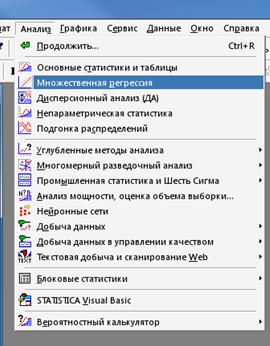
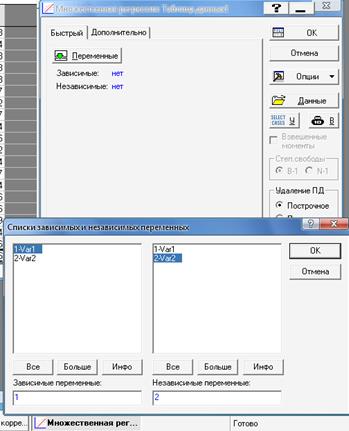
Рис. 7 – Окно «Множественная регрессия».
После выбора переменных и вывода необходимых характеристик появляется итоговое окно (рис.8), содержащее основные характеристики уравнения регрессии: множественный коэффициент корреляции, стандартные ошибки.
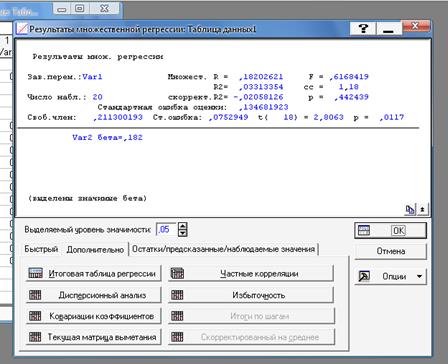
Рис.8 – Итоговое окно «Множественная регрессия»
Для вывода значения коэффициентов регрессии активизируют кнопку «Summary: regression results», находящаяся в нижнем левом углу, после чего появляется окно вывода данных (рис.9). Красным выделяются значимые коэффициенты регрессии с вероятностью, указанной над вычисленными характеристиками.
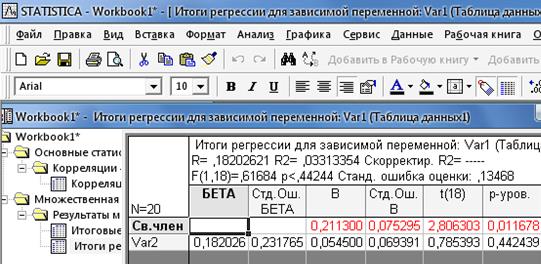
Рис.9 – Вывод значений коэффициентов регрессии.
Коэффициенты регрессии находятся в Excel с помощью меню «Сервис», функции «Анализ данных», и в предложенном списке методов анализа - метод «Регрессия», где заполняют «входной интервал У», «входной интервал Х», «выходной интервал», «Уровень надежности» и нажимают «ОК» (рисунок 10).
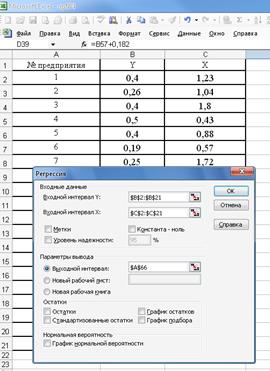
Рисунок 10- Ввод данных для вычисления коэффициентов регрессии.
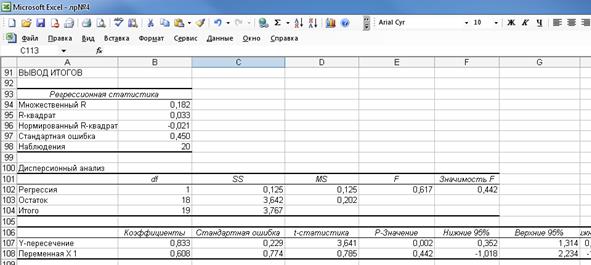
Вывод итогов (рисунок 11) состоит из трех таблиц: в верхней указаны показатели качества построенного уравнения, в средней – дисперсионный анализ, в нижней - коэффициенты регрессии (у- пересечение – это свободный член уравнения, «переменная х» – значение коэффициента регрессии при переменной х). Границы доверительных интервалов находятся в нижней таблице – на пересечении столбцов «нижние 95%», «верхние 95%» и соответствующих строк – «у – пересечение» и «переменная х».
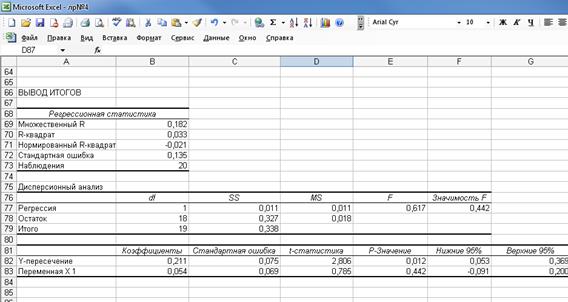
Рисунок 11 – Вывод итогов меню «Регрессия»
Уравнение регрессии для рассматриваемого примера (см.рисунок 11) имеет вид:
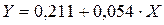
Значимость построенного уравнения регрессии можно проверить посредством средней таблицы – дисперсионного анализа, в предпоследнем и последнем столбцах которой указываются значение статистики F и вероятность принятия нулевой гипотезы (столбец значимость F). Если эта вероятность имеет значение значительно меньшее уровня 0,05, то делают вывод, что построенное уравнение значимо. В нашем случае уравнение не значимо, т.к. значимость F – 0,442
На основании расчетных данных доверительный интервал для коэффициента регрессии имеет вид (см. рисунок 11):
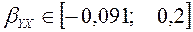
Аналогично для уравнения Х на Y (в меню «Регрессия» меняем входной интервал X и входной интервал Y местами):
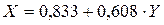 - уравнение также является значимым
- уравнение также является значимым
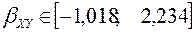
Вывод: анализируя построенные уравнения регрессии, можно сказать, что: при изменении величины Х на одну единицу аргумент Y увеличится на 0,054 единицы (для первого уравнения). И аналогично для второго: при изменении Y на 1 единицу величина Х увеличится на 0,608.
при увеличении удельного веса покупных изделий на одну единицу премии и вознаграждения на одного работника увеличатся на 0,054 единицы (для первого уравнения). И аналогично для второго: при увеличении премии и вознаграждения на одного работника на 1 единицу удельный вес покупных изделий увеличится на 0,608ед.
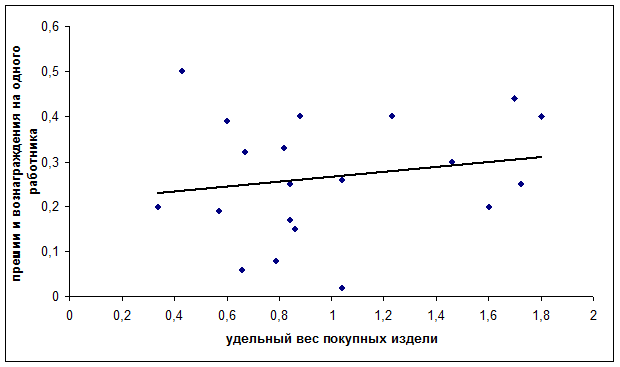
Нанесем полученные уравнения на графики:
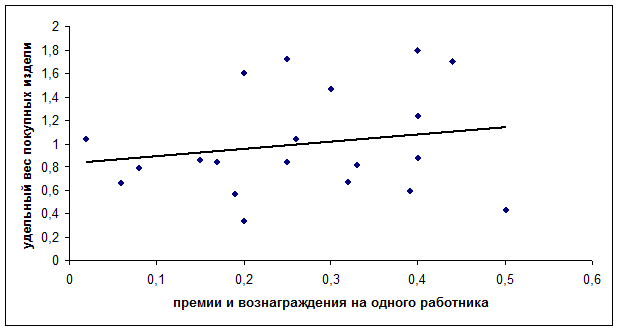
Задание: С целью анализа взаимосвязи показателей эффективности производства продукции: производительности труда и фондоотдачи была отобрана группа 20 однотипных машиностроительных предприятий. На основании годовых отчетов предприятий были получены следующие данные (таблица 1):
Х – удельный вес покупных изделий;
У – премии и вознаграждения на одного работника.
Провести корреляционный анализ показателей эффективности работы предприятий: вычислить парный коэффициент корреляции, оценить его значимость, построить доверительный интервал, построить уравнение регрессии У на Х и Х на У. Сделать выводы.
Таблица 1. – Показатели производительности предприятий
| № предприятия | Y | X |
| 0,40 | 1,23 | |
| 0,26 | 1,04 | |
| 0,40 | 1,80 | |
| 0,50 | 0,43 | |
| 0,40 | 0,88 | |
| 0,19 | 0,57 | |
| 0,25 | 1,72 | |
| 0,44 | 1,70 | |
| 0,17 | 0,84 | |
| 0,39 | 0,60 | |
| 0,33 | 0,82 | |
| 0,25 | 0,84 | |
| 0,32 | 0,67 | |
| 0,02 | 1,04 | |
| 15 | 0,06 | 0,66 |
| 0,15 | 0,86 | |
| 0,08 | 0,79 | |
| 0,20 | 0,34 | |
| 0,20 | 1,60 | |
| 0,30 | 1,46 |
Х6 – удельный вес покупных изделий;
Х8 – премии и вознаграждения на одного работника;
