Биномиальное распределение
Закон распределения СВ 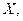 задаваемый формулой Бернулли
задаваемый формулой Бернулли
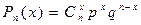
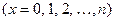 ,
,
называется биномиальным распределением с параметрами 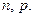
Этому закону подчиняется, например, СВ 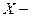 число появлений герба при 4 бросаниях монеты.
число появлений герба при 4 бросаниях монеты.
2. Распределение Пуассона.
Закон распределения СВ 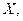 задаваемый формулой Пуассона
задаваемый формулой Пуассона
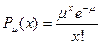
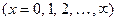
называется распределением Пуассона с параметром 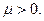
Этому закону подчиняется, например, СВ 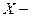 число рождений за год двух близнецов в г. Октябрьском.
число рождений за год двух близнецов в г. Октябрьском.
22. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА.
Случайная величина называется непрерывной, если её возможные значениязаполняют целиком интервал, конечный или бесконечный.
В примере 2 раздела 18 была дана непрерывная СВ.
За д а ч а 1. Дана функция распределения непрерывной СВ 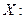
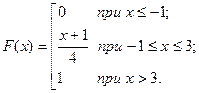
Постройте её график и найдите вероятности событий 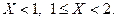
□ СВ 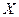 может принимать любые значения из интервала
может принимать любые значения из интервала 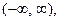 поэтому
поэтому 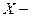 непрерывная СВ. Строим график функции
непрерывная СВ. Строим график функции 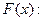
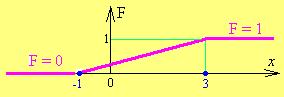
Рис. 22.1
Находим вероятности событий:
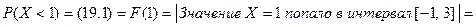
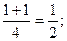
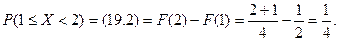 ■
■
22. ПЛОТНОСТЬ ВЕРОЯТНОСТИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Пусть 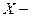 непрерывная СВ, а её функция распределения
непрерывная СВ, а её функция распределения 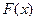 имеет производную
имеет производную 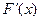 всюду, кроме, быть может, отдельных точек.
всюду, кроме, быть может, отдельных точек.
Функция 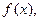 определяемая формулой определяемая формулой |
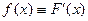 |
называется плотностью вероятности случайной величины 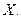 |
(23.1)
График функции 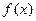 называют кривой распределения.
называют кривой распределения.
Из формулы (23.1) вытекает, что
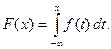 (23.2)
(23.2)
¨ 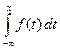 = (23.1) =
= (23.1) = 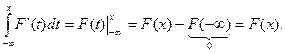 ■
■
Итак, если дана функция 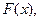 то по формуле (23.1) можно найти
то по формуле (23.1) можно найти 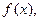 а если дана функция
а если дана функция 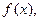 то по формуле (23.2) можно найти
то по формуле (23.2) можно найти 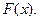
За д а ч а 1. Дана функция распределения непрерывной СВ 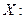
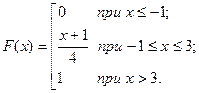
Найдите плотность вероятности 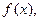 постройте графики функций
постройте графики функций 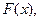
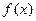 и найдите вероятности событий
и найдите вероятности событий 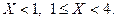
□ Воспользуемся формулой (23.1):
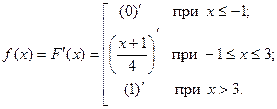
Отсюда
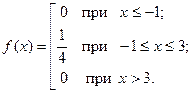
Строим графики функций 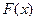 и
и 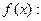
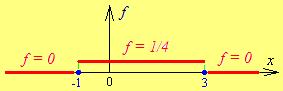
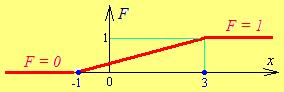
Рис. 23.1 Рис. 23.2
Находим вероятности событий:
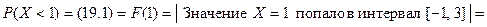
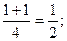
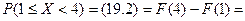
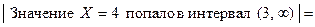
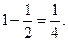 ■
■
Отметим свойства плотности вероятности:
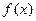 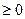 | График плотности вероятности располагается выше оси 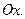 |
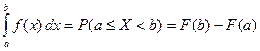 | Площадь под графиком 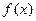 на участке на участке 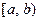 равна вероятности попадания СВ равна вероятности попадания СВ 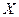 на этот участок (рис. 23.1). на этот участок (рис. 23.1). |
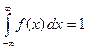 | Вся площадь под графиком 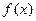 равна 1 (рис. 23.2). равна 1 (рис. 23.2). |
(23.3)
(23.4)
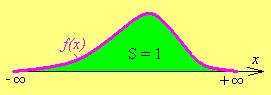
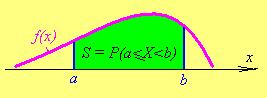
Рис. 23.1 Рис. 23.2
¨ 1) 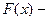 неубывающая функция, поэтому
неубывающая функция, поэтому 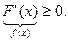
2) 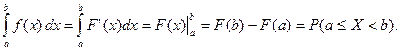
3) 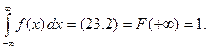 ■
■
Если вы имеете функцию 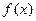 или
или 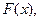 значит, вы имеете закон распределения непрерывной СВ.
значит, вы имеете закон распределения непрерывной СВ.
З а д а ч а 2. СВ 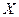 имеет плотность вероятности
имеет плотность вероятности 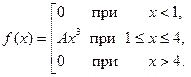
Найти постоянную 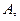 функцию
функцию 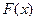 и построить графики
и построить графики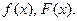
□ Находим  из условия (23.4):
из условия (23.4): 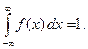
В этой задаче 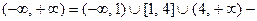 три участка, поэтому
три участка, поэтому
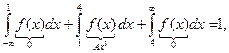
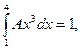
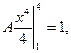
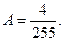
Значит, функция 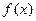 такова:
такова:
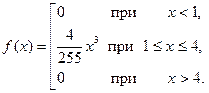
График этой функции показан на рис. (23.3).
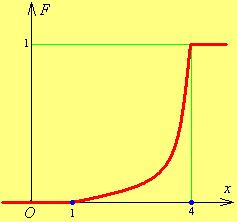
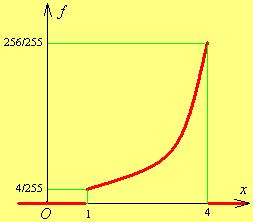
Рис. 23.3 Рис. 23.4
Приступим к определению функции 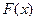 на каждом из трёх участков оси
на каждом из трёх участков оси 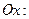
при 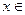
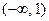 имеем
имеем 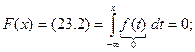
при 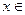
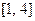 будет
будет 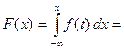
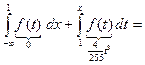
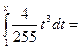
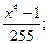
при 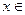
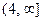 получаем
получаем 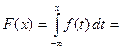
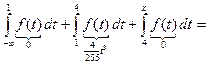
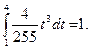
Следовательно, функция 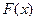 такова:
такова:
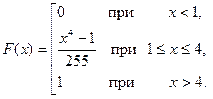
График этой функции показан на рис. 23.4. ■
Вопросы к экзаменам
1. Понятие случайной величины. Дискретные и непрерывные случайные величины.
2. Закон распределения вероятностей дискретной случайной величины.
3.Биномиальное распределение.
3.Распределение Пуассона.
3.Математическое ожидание дискретной случайной величины и его свойства.
4.Дисперсия дискретной случайной величины и её свойства. Среднее квадратическое отклонение.
5.Корреляционный момент. Коэффициент корреляции.
6.Корреляционная таблица. Выборочный коэффициент корреляции.
7.Выборочное корреляционное отношение.
