Сплайндар арқылы жуықтау

Сплайн деп - 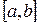кесіндісінде бірнеше туындылары мен бірге үздіксіз болған әртүрлі көпмүшеліктердің үзідіктерден құрастырылған полиномдық функцияны айтады. Практикада сызықтық, параболалық және кубтық сплайндар қолданылады.

Сызықтық сплайндар

Сызықтық сплайн сынық сызықты көрсетеді. Интерполяцияланатын функция 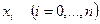торында өзінің 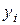мәнімен берілген болсын. 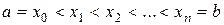. Әрбір 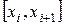интервал үшін 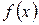функция сызықтық функциямен алмастырылады.

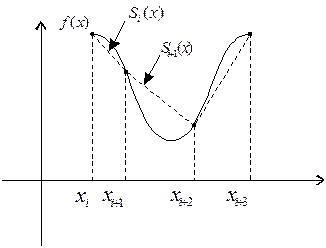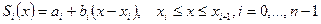. (6.7.1)

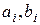сплайн коэффициенттері келесі шарттардан табылады:

1) түйіндер торындағы сплайн мәні функция мәнімен сәйкес келеді 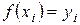, сонымен қатар

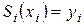; (6.7.2)

2) Түйіндер торында сплайн үздіксіз болуы қажет, сонымен қатар

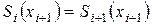; (6.7.3)

Бірінші шарт бойынша 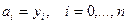табамыз; екінші шарт бойынша мынаны аламыз

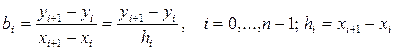. (6.7.4)

Параболалық сплайндар

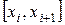әрбір интервалында 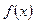функциясы квадраттық функция түрінде интерполяцияланады

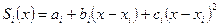(6.7.5)

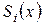
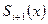
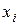
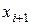
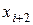
(6.7.5)-тен 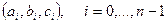коэффициенттері анықталады. Олардың саны - 3n:

1) Тордың түйіндерінде сплайн мәні 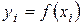( (5.2.2) ні қараңыз) интерполяцияланушы функция мәнімен сәйкес келеді;

2) Тордың түйіндерінде сплайн үздіксіз болуы қажет (5.2.3) ;

3) Тордың түйіндерінде бірінші туынды үздіксіз болуы қажет, сонымен қатар

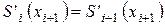. (6.7.6)

Бірінші шарттан мынаны аламыз

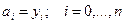. (6.7.7)

Үшінші шарттан мынаны аламыз

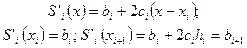(6.7.8)

Мұндағы

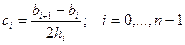. (6.7.9)

Екінші шарт бойынша

,

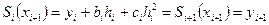Сондықтан былай болады

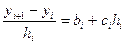. (6.7.10)

(6.7.9)-ды (6.7.10)-ға қою арқылы, мынандай теңдеу жүйесіне келеміз

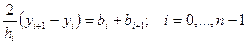. (6.7.11)

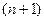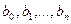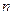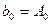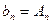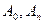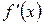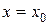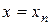белгісізді анықтау үшін теңдеуі бар. Сондықтан да шекаралық шартын қою қажет. , немесе , мұнда - - функция бірінші ретті туындысының және нүктесіндегі мәні.

Егер 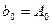мәні белгілі болса, онда (6.7.10)-нан:

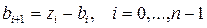. (6.7.12)

Егер 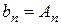белгілі болса, онда (6.10.11) алгоритмі жалғасады

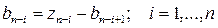. (6.7.13)

(6.7.12), (6.7.13) формулаларынан мынау алынады

.

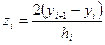Кубтық сплайндар

Келесі түрде кубтық сплайнды құрамыз: Әрбір 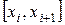интервалында 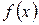функциясын полиноммен аппроксимациялаймыз.

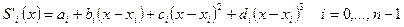, (6.7.14)

Мұнда 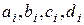-анықталуы қажет сплайн коэффициенттері (барлығы 4n коэффициенттері бар).

Сплайн коэффициенттерін келесі шарттар арқылы анықтаймыз:

1) Түйін нүктелердегі сплайн мәні 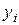-мен сәйкес келеді;

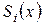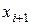2) мәні түйінінде 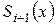сәйкес келеді (үздіксіз сплайн шарты);

3) 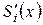туындының мәні 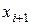түйінінде 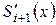сәйкес келеді (бірінші туындының үздіксіздік шарты);

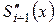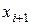4) мәні түйінінде 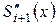-пен сәйкес келеді (екінші туындының үздіксіздік шарты)

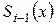
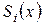
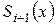
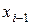
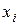
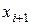
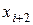
Бірінші шарттан мынаны аламыз

,

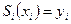Бұл жерден 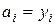. (6.7.15)

Төртінші шарттан мынаны аламыз

.

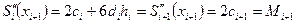мұндағы

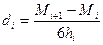. (6.7.16)

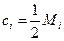. (6.7.17)

Үшінші шарттан мынаны аламыз

.

мұнда

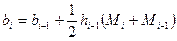. (6.7.18)

Екінші шарттан мынаны аламыз

.

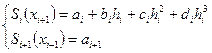Бұл жерден 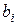үшін (6.7.16) және (6.7.17) ескере отырып мынаны аламыз

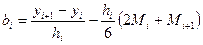. (6.7.19)

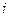индексін 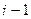-ге қоямыз

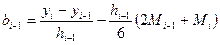. (6.7.20)

(6.10.20)-ны (6.10.18)-ге қою арқылы мынаны аламыз,

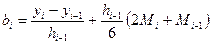. (6.7.21)

(6.7.15), (6.7.16), (6.7.17), (6.7.21) сплайн коэффициенттерінің мәнін (6.7.14)-ке қою арқылы мынаны аламыз:

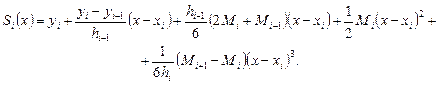(6.7.22)

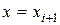-ді 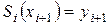теңдігіне қою арқылы 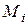-ге қатысты белгісіз сызықтық теңдеулер жүйесін аламыз:

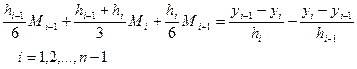. (6.7.23)

Мұнда .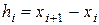

Бұл жүйе 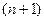белгісізді 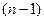теңдеуінен тұрады. Сондықтан екі белсізді анықтауымыз қажет. Ол үшін шеаралық шартын қоюмыз қажет:

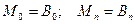. (6.7.24)

Келесі анықтауларды жүргіземіз:

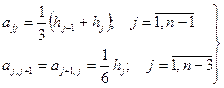(6.7.25)

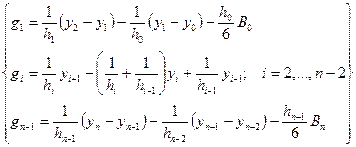(6.7.26)

(6.10.23) жүйе матрицалық түрде былай жазылады

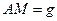, (6.7.27)

(6.7.25) формуласымен 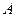- 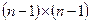элементті үш диагональды симметриялық матрица және 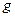- - 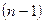векторы мен (6.7.26) элементтері арқылы анықталады.

(6.10.27)-ден 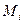мәнін есептеу арқылы, содан соң (6.7.15), (6.7.16), (6.7.17) және (6.7.19) формулаларынан 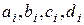сплайн коэффициенттерін анықтаймыз.

Егер бірінші туынды шартының шегі белгілі болса,

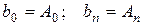, (6.7.28)

онда (6.7.23) жүйесіне тағы екі теңдеуді қосамыз. Бірінші теңдеу 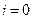шартында (6.7.19)-дан алынады, екінші теңдеу 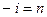шартында (6.7.21)-ден алынады. Нәтижесінде (6.7.23)-тің орнына мына жүйені аламыз

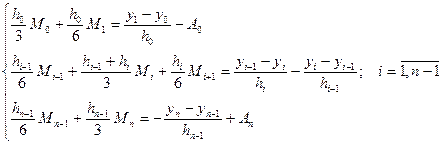(6.7.29)

Бұл жүйе 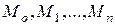белгісізді 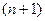теңдеуелер жүйесі (6.7.29) жүйе үш диагональды және матрицасы симметриялық.

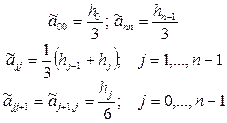(6.7.30)

компоненттермен 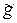векторын жүргіземіз.

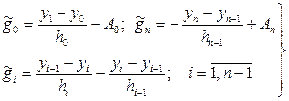(6.7.31)

(6.7.30) және (6.7.18) қатысты (6.7.16) жүйесін матрицалық түрде былай жазуға болады

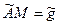. (6.7.32)

Білімін тексеру сұрақтары:

1. Нүктелік квадраттық аппроксимцияның мазмұны неде?

2. Сплайнға анықтама беріңіз. Қандай сплайндар сізге белгілі?

3. Сплайндар коэффициенттерін табу шарттарын атаңыз: а)сызықтық; б) квадраттық; в) кубтық.

4. Сызықтық сплайнға анықтама беріңіз.

5. Квадраттық сплайнға анықтама беріңіз.

6. Кубтық сплайндарға анықтама беріңіз.

7. Параболалық сплайндарға анықтама беріңіз.

8. Берілген кесіндіде функцияны интегралдық квадраттық аппроксимациялау деген не?

9. Берілген кесіндіде функцияны квадраттық апроксимациялау деген не?

10. Аппроксимациялаушы немесе жуықтаушы полином деп қандай полиномдыайтамыз.