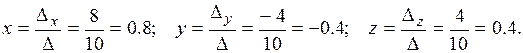Решение систем линейных уравнений методом Крамера
Метод Крамера, как и матричный способ, применяется для решения систем n линейных уравнений c n неизвестными при условии, что основной определитель системы не равен нулю:
det A = D ¹ 0.
Рассмотрим систему n линейных уравнений c n неизвестными вида (1).
Пусть А - основная матрица системы (матрица, составленная из коэффициентов при неизвестных).
Рассмотрим определители:
; 
;
; ... ; 
.
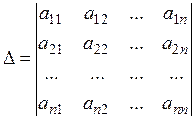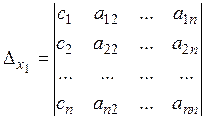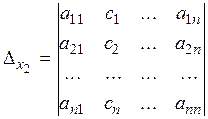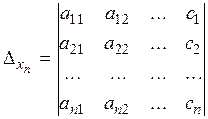Определители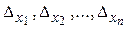 
получаются из определителя системы D заменой свободными членами элементов соответственно первого, второго, ..., n -го столбцов.
Если det A = D ¹ 0, то существует, и притом единственное, решение этой системы, которое вычисляется по формулам Крамера:
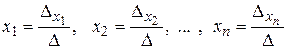. (4)
Пример.Решите систему уравнений методом Крамера:
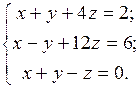
Решение. 1) Вычислим det A = D =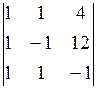 
= 10.
2) Вычислим вспомогательные определители:
Dх =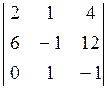 
= 2 + 24 – 24 + 6 = 8; Dу = 
=
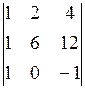= - 6 + 24 – 24 +2 = - 4; Dz =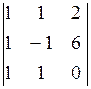 
= 2 + 6 + 2 – 6 = 4.
3) Найдём неизвестные по формулам Крамера (4):
