Основные случаи вычисления двойного интеграла в прямоугольных координатах

Практическое занятие № 14

«Вычисление двойных интегралов в случае областей 1 и 2 типа»

1. Цель: Выработать вычислительные навыки на действия с функциями нескольких действительных переменных

2. Пояснения к работе:

2.1 Краткие теоретические сведения:

Определение двойного интеграла

Пусть в замкнутой ограниченной области D плоскости хОу определена непрерывная функция z=f(x, у). Разобьем область D произвольным образом на n частичных областей с площадями ΔS1, ΔS2, .., ΔSn. В каждой i-й элементарной области ΔSi- выбе­рем произвольную точку Мi (хi, yi), умножим значение функции в этой точке f(xi, yi) на площадь ΔSi- соответствующей области и составим сумму этих произведений, т.е. 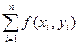ΔSi, которая называется интегральной суммой функции f(x, у) в области D.

Двойным интегралом функции f(x, у) по области D называется предел этой суммы:

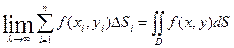(1)

где λ — наибольший из диаметров элементарных областей ΔSi-. Функция z=f(x, у), для которой предел (1) существует и конечен, называется интегрируемой в этой области.

В прямоугольных координатах дифференциал площади dS=dx dy, тогда двойной интеграл примет вид

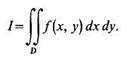
(2)

Если f(x, у)>0, то двойной интеграл функции z=f(x, у) по области D равен объему тела, ограниченного сверху поверхностью z=f(x, у), сбоку цилиндрической поверхностью, образующие которой параллельны оси Oz, a направляющей служит контур фигуры D, и снизу плоскостью z=0.

Основные свойства двойного интеграла

1˚. Двойной интеграл от алгебраической суммы функций равен алгебраической сумме двойных интегра­лов от слагаемых функций:

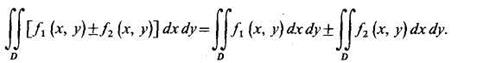
2˚ . Постоянный множитель можно выносить за знак двойного интег­рала:

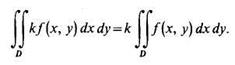
3°. Область интегрирования двойного интеграла можно разбить на части, т. е. если область состоит из двух областей D₁ и D₂, то

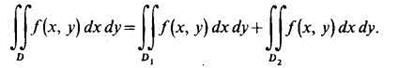
Основные случаи вычисления двойного интеграла в прямоугольных координатах

1) Если область D, в которой рассматривается двойной интеграл (2), есть прямоугольник со сторонами, параллельными координатным осям и заданными уравнениями х = а, x = b

(a ≤ x ≤ b), у = с, y=d (c≤ y ≤ d) то двойной интеграл вычисляется по одной из формул

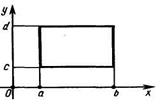
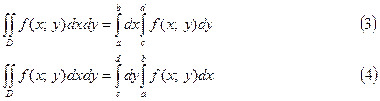
Интегралы в правых частях формул (3) и (4) называются повторными (или двукратными), а интегралы 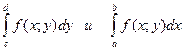называются внутренними.

Под символом 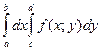формуле (3) подразумевается дважды произведе­нное интегрирование. Первое интегрирова­ние (внутреннее) по переменной у совершает­ся в пределах от с до d в предположении, что х остается постоянным; результат интег­рируется по переменной х в пределах от а до b. Если вычисление двойного интеграла выполняется по формуле (4), то порядок интегрирования меняется; внутренний интеграл вычисляется по переменной х, причем у сохраняет постоянное значение, а внешнее (повторное) интегрирование производится по переменной у.

2) Если область D такова, что любая прямая, проходящая внутри этой области и параллельная оси Оу, пересекает ее границу в двух точках (см. рисунки ниже), то эта область называется простой относительно оси Ох и определяется системой неравенств вида

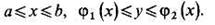
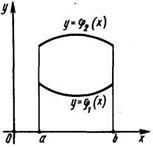
В этом случае двойной интеграл выражается через повторный интеграл по формуле:

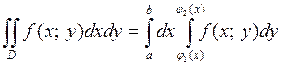(5)

3) Если граница области D пересекается в двух точках всякой прямой, проходящей внутри этой области и параллельной оси Ох (рис. 4, то эта область называется простой относительно оси Оу и определяется системой

неравенств вида

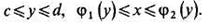
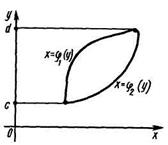
В этом случае двойной интеграл выражается формулой:

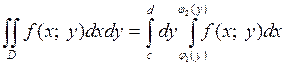(6)

где интегрирование сначала выполняется по переменной х, а затем по переменной у.

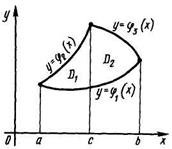4) Если нижняя или верхняя линии границы состоят из нескольких участков, имеющих различные уравнения, то область D необходимо разбить прямыми, параллельными оси Оу, на такие части, чтобы каждый из участков выражался одним уравнением. В этом случае вычисление двойного интеграла сводится к вычислению двух (и более) повторных интегралов.

В случае, изображенном на данном рисунке, область D₁ определяется системой неравенств а ≤ х ≤ с, φ₁ (x)≤ y ≤φ₂(x), а область D2 — системой неравенств с ≤ х ≤ b, φ₁ (x )≤ y ≤ φ₃(x), и, значит,

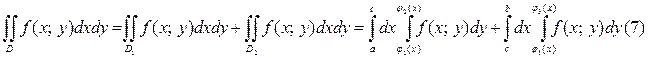
Пример 1. Вычислить повторный интеграл: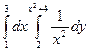

Решение: Согласно формуле (6), имеем

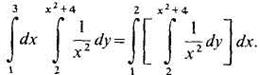
Вычислим сначала внутренний интеграл по переменной у, считая х постоянным:

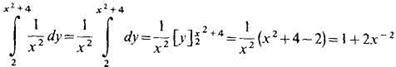
Теперь вычислим внешний интеграл по переменной х, подставив в него полученное выражение:

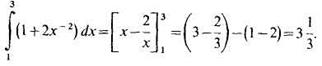
Пример 2. Вычислить двойной интеграл 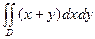по области D, ограниченной прямыми х = 2, x = 6, y=1 и у = 4.

Решение: Область D является простой отно­сительно осей Ох и Оу, поэтому для вычисления интеграла можно использовать любую из формул (3) или (4).

Сначала вычислим двойной интеграл по формуле (3):

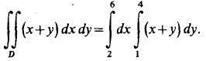
Вычислив внутренний интеграл по переменной у при постоянном х, находим

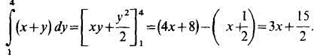
Подставив это выражение во внешний интеграл, получим

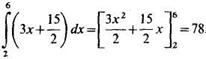
Теперь вычислим двойной интеграл по формуле (4):

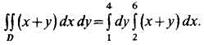
Найдем внутренний интеграл:

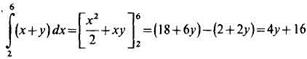
Далее найдем внешний интеграл:

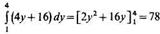
т. е. получили тот же ответ.

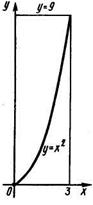
Пример 3. Вычислить двойной интеграл 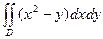по области D, заданной системой неравенств 0 ≤ х ≤ З; ≤ y ≤ 9

Решение: область D является простой как относительно оси Ох, так и относительно оси Оу; поэтому вычислим этот интеграл двумя способами. Произведем вычисление по формуле (5). Пределами внутреннего интегра­ла являются функции у=

и у=9, составляющие уравнения нижней и верхней границ области D, а пределами внешнего интеграла являются абсциссы х=0 и х - 3. Значит,

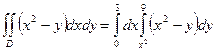
Вычислим внутренний интеграл по переменной у в предположении,

что х - постоянная:

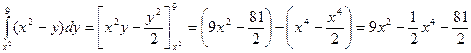
Вычислим внешний интеграл:

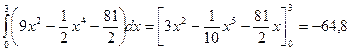
Произведем теперь вычисление по формуле (6). В этом случае область D выражается системой

неравенств 0 ≤ у ≤9, 0 ≤ x ≤ 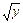, т. е. пределами внут­реннего интеграла служат функции х = 0 и x= 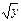, а пределами внешнего интеграла — ординаты у=0 и у = 9. Поэтому

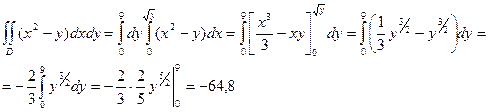
Задание

Вариант 1

1. Вычислите повторный интеграл:

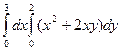
2. Вычислите двойной интеграл, где D — область, ограниченная параболами у=х² и х=у²

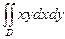
3. Измените порядок интегри­рования в двойном интеграле: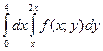

Вариант 2

1. Вычислите повторный интеграл: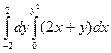

2. Вычислите двойной интеграл ,где D — область, ограниченная линиями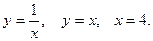

3. Измените порядок интегриро­вания в двойном интеграле: ;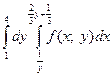

Вариант 3

1. Вычислите повторный интеграл: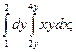

2. Вычислите двойной интеграл 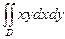, где D — область, oгpaничейная линиями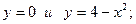

3. Измените порядок интегриро­вания в двойном интеграле: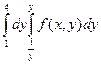

Вариант 4

1. Вычислите повторный интеграл: ;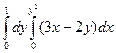

2. Вычислите двойной интеграл 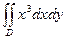, где D — область, oгpaничейная линиями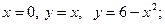

3. Измените порядок интегриро­вания в двойном интеграле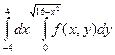

4. Контрольные вопросы:

1.Дайте определение двойного интеграла;

2. Какие свойства двойных интегралов вы знаете?

3. Что такое повторные интегралы?

4. Какая область называется простой относительно оси ОХ, относительно оси ОУ?

5. Содержание отчёта:

5.1 Наименование работы

5.2 Цель работы

5.3 Задание

5.4 Формулы для расчета

5.5 Необходимые расчеты. Анализ результатов расчетов

5.6 Выводы по работе

5.7 Ответы на контрольные вопросы

6. Литература:

1. Подольский В. А. Сборник задач по математике: Учебное пособие - М. Высшая школа, 2003, с.361-375;

2. Богомолов Н.В. «Практические занятия по математике» - Учебное пособие – М.:Высш. школа, 2003, с.439-454.