Обчислення аргументу
Спочатку відмітимо властивість: 
1) Аргумент дійсного і чисто уявного числа : якщо  , то
, то 
2) Аргумент будь-якого числа  можна знаходити за формулою:
можна знаходити за формулою:
 (1.1)
(1.1)
Доведемо останню формулу у випадку, коли  зображується точкою
зображується точкою  в другій чверті (рис.1.7). З
в другій чверті (рис.1.7). З 
 . Оскільки
. Оскільки  , то
, то 
 |
Рис 1.7
Інші випадки розміщення числа 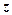 на площині розглядаються аналогічно.
на площині розглядаються аналогічно.
Зауважимо, що вказаним способом для аргументу можна одержати формули, в яких використовуються арккотангенс, арккосинус чи арксинус.
Якщо не вимагається високої точності, то аргумент к.ч. можна знаходити графічно. З цією метою слід побудувати к.ч. на міліметровому папері і виміряти відповідний кут за допомогою транспортиру. Цей спосіб іноді використовують для грубої перевірки обчислень.
Приклад 1.Покажемо, як обчислюють аргументи чисел  за допомогою формул цього пункту.
за допомогою формул цього пункту.
 , (застосована формула (1.1),
, (застосована формула (1.1),  чверті);
чверті);
 , ( формула (1.1),
, ( формула (1.1),  чверті);
чверті);
 , (формула (1.1) ,
, (формула (1.1) ,  чверті);
чверті);
 , (формула (1.1) ,
, (формула (1.1) ,  чверті);
чверті);
Приклад 2. Достатньо встановити знаки дійсної і уявної частин к.ч., щоб перевірити рівності:
 ,
,
 .
.
