Разомкнутая СМО с ожиданием
Поток требований, поступающих в n–канальную СМО с неограниченной очередью, имеет интенсивность λ, а поток обслуживаний одной заявки – интенсивность:
 .
.
Граф состояний такой системы представлен на рис. 8.3.

Рис. 8.3. Граф состояний разомкнутой СМО с ожиданием
Рассмотрим расчет характеристик (показателей качества функционирования) разомкнутой СМО.
1. Для нормального функционирования системы необходимо соблюдение требования n > 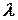
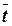 об (в противном случае очередь будет расти неограниченно), где п– количество обслуживающих каналов (аппаратов);
об (в противном случае очередь будет расти неограниченно), где п– количество обслуживающих каналов (аппаратов); 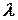 – интенсивность поступления требований в систему;
– интенсивность поступления требований в систему; 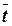 об – средняя продолжительность обслуживания одного требования одним аппаратом.
об – средняя продолжительность обслуживания одного требования одним аппаратом.
2. Вероятность того, что в системе находится k требований при условии, когда их число не превышает числа обслуживающих аппаратов:
Pk=akP0, (0 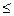 k
k 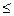 n),
n),
ak=  (
( 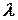
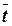 об)k,
об)k,
где Р0 – вероятность того, что все обслуживающие аппараты свободны.
3. Вероятность того, что в системе находится k требований при условии, когда их число превышает число обслуживающих аппаратов:
Pk=akP0, (k > n),
ak=  (
( 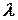
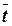 об)k.
об)k.
4. Вероятность того, что все обслуживающие аппараты свободны:
P0=  .
.
5. Вероятность того, что обслуживающие аппараты заняты (вероятность отказа в немедленном обслуживании):
Pотк=Pn  =Pn
=Pn  .
.
6. Средняя длина очереди:
A1=  = Pn.
= Pn.  .
.
7. Средняя продолжительность ожидания обслуживания (продолжительность простоя в очереди)
Tож=A1  =Pn
=Pn  .
.
8.Среднее число требований, находящихся в системе (обслуживаемых и ожидаемых обслуживания):
А2 = Р1 + 2Р2 + 3Р3 +…+ (n – 1) Рn-1 +nРn (n/(n - 
 об)) + A1.
об)) + A1.
9. Среднее число свободных аппаратов:
A3=  .
.
10. Коэффициент простоя обслуживающего аппарата:
a3=  .
.
Пример 2. Центральный склад фирмы отпускает материалы не только филиалам фирмы, но и сторонним организациям, число которых заранее неизвестно. Представители сторонних организаций могут повторно на склад не прибыть, поскольку договорные отношения могут завершиться или прерваться с одними контрагентами и начаться с другими. Поэтому центральный склад можно считать разомкнутой (открытой) системой с неограниченным входящим потоком.
Проведенный анализ показал, что входящий на склад поток автомашин за материалами является пуассоновским, а за один час на склад в среднем прибывает 1,75 автомашины. На складе имеются два автопогрузчика, которые используются только для погрузки материалов на пребывающие автомашины. Средняя продолжительность погрузки одной автомашины одним автопогрузчиком составила 48 мин. Продолжительность погрузки одной автомашины подчиняется показательному закону распределения. Если прибывшая автомашина застает оба автопогрузчика занятыми, то она становится в очередь. Анализ также показал, что продолжительность ожидания (простоя в очереди) подчиняется показательному закону распределения.
Решение. Рассчитаем основные параметры системы для условий задачи.
Прежде всего проверим выполнение условия п > 
 об. Так как 2>1,75
об. Так как 2>1,75  0,8 = 1,4, то система может нормально функционировать.
0,8 = 1,4, то система может нормально функционировать.
Вероятность того, что на складе нет автомашин:
Р0=  1,4Р0=Р0.
1,4Р0=Р0.
Вероятность того, что на складе одна автомашина:
P1=  1,4P0=1,4P0.
1,4P0=1,4P0.
Вероятность того, что на складе две автомашины:
P2=  1,42P0=0,98P0.
1,42P0=0,98P0.
Вероятность отказа в немедленном обслуживании (вероятность возникновения очереди):
Pотк=P2  =0,98P0
=0,98P0  =3,2667P0.
=3,2667P0.
