Теорема сложения скоростей при сложном движении точки

Скорость точки относит НСО наз. абсолютной Vабс (Va).Скорость точки относит ПСО наз. относительной Vотс (Vr).Скорость которую имела бы точка находясь в данном положении движущегося тела при отсутствии относит. Движ. Наз. переносная скорость движ. Vпер (Vc). Теор. абсолют скорость точки равна геометр. Сумме относит. и перенос. Скорости Va=Vr+Vc. Док. Пусть точка М приходит в полож М₃ двигаясь по троектории обсолютного движения.(Рис в 4.1).Для определения Vr необход мысленно остановить переносное движ_. Для опред Ve необход мысленно остановить относительное движ. Поэтому для опред. абсолют. Скорости точ. Необход снач. Опред. Полож. Точ. В требуемый момент времени на троектории относит движ.

25.Теорема сложения ускорений при сложном движении точки. Ускорение Кориолиса. Определение направления ускорения Кориолиса. Правило Жуковского. Смысл ускорения Кориолиса.

1) Переносное движение поступательно. Абсолютное ускорение точки равна геометрич. Сумме относит и переносного движ a_a=a_r+a_e . Если относит движение движ по криволинейной троектории то a_a= a_rⁿ + a_r ^t+a_e.Для определения относит ускорения нужно остановить переносное движение. Для определения переносного ускорения нужно остановить относительное движение.

2)Обсолютное ускорение точки при не поступательном переносном движении равна геометрич сумме a_a=a_r+a_e+ a_с

Кариолисово ускорение характер:1)Изменение велечины переносной скорости в следствии относит движения.2)Изменением направления вектора относит скорости в след непоступательного переносного движ. . a_с =2 a_сώ_e Vrsin(ώ_r,Vr)

Кариолисово ускорение опред по правилу векторного произведения. . a_{с┴ (}ώ_e, Vr) и направлено таким образом чтоб смотря ему навстречу поворот от ώ_e к Vr на найменьший угол происходит против часовой стрелки.

Сложное движение твердого тела. Сложное поступательное движение.

Сложным наз такой вид движ тела при котром оно одновременно участвует в 2 или более двужениях.

Рвссмотрим движ твердого тела движ относит подвиж тела со скорость V1 которое в свою очередьдвиж поступател со скоростью V2.Т.к скорость точек А и В одинаковы то результирующая при сложении движ поступательна то движ также будет поступате со скоростью равной векторной сумме относительной и посткпательной скорости.(Рис в 7.1)

Vав=Vra+Vеа=V1+V2 Vав=Vrв+Vев=V1+V2 V=V1+V2

Сложение одинакого направленных вращений вокруг параллельных осей.

1)сложение одинакого направленных движений.При сложении 2 один направ движ результир яв вращ движ вокруг оси проходящей пареллельно оси вращения через точку делящую отрезок между осями относит и переносного вращения внутренним образом на части обратно пропорционально угловым скоростям составляющим вращения

Vав=Vr+Vе Vав=0=Vr+Vе=> Vr= - Vе Vе=ω1*OB Vr=ω2*AB

ω1*OB= ω2*AB ω1/ AB= ω2/ OB=ω/OA (рис в 7.2)

2)Сложение вращ движ направ противоположно вокруг направленных осей. При сложении 2 противоположно направленных вращений с разными угловыми скоростями результирущая яв вращ движ вокруг мгновенной оси проходящей параллельно осям состовляющим вращение через точку делящую отрезок заключенный между осями внещним образом на части обратнопропорционол угловым скоростям состав вращ

Угловая скорость результирующего вращ равна разности угловых скоростей и состав вращ.( рис в 7.2) ω1≠ ω2

Vав=Vr+Vе Vе= ω1*OB Vr = ω2*AB Vе(со штрихом)= ω1² *OA

ω= ω1- ω2 ω1/AB= ω2/OB=ω/OA

Сложение противоположно направленных вращений вокруг параллельных осей.

В этом случаи будет поступательное движ со скоростью равной векторному произведению одного из составляющих движ на вектор соед точки проходящте через оси состав вращ (рис в 7.2)

Vав=Vr+Vе ρ=OA+r_B OA=ρ+r_B Vr= ω2× r_B Vе= ω1+ ρ

Vав=ω2× r_B +ω1× ρ= ω2× r_{B --} ω2×ρ= ω2(r_B- ρ)= ω1×( ρ- r_B )= ω1×OA

( везде в формуле сверху векторы)

Пара вращений

3) Пара вращений – вращения вокруг ||-ных осей направлены в разные стороны и угловые скорости по модулю равны ( 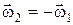– пара угловых скоростей). В этом случае v_A=v_B, результирующее движение тела – поступательное ( или мгновенное поступательное) движение со скоростью v=w₁×AB – момент пары угловых скоростей (поступательное движение педали велосипеда относит-но рамы). Мгн. центр скоростей находится в бесконечности.