Сложение скоростей и ускорений при сложном движении точки

Не останавливаясь на доказательстве, сформулируем и обсудим содержание двух основных теорем теории сложного движения точки. (Доказательства этих теорем приведены в учебнике.....)

Для вычисления абсолютной скорости точки получается вполне ожидаемый результат:

абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:

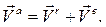(3.1)

Абсолютное ускорение точки вычисляется при помощи теоремы Кориолиса:

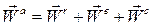(3.2)

где вектор

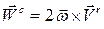(3.3)

называется ускорением Кориолиса.

Таким образом,

абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений.

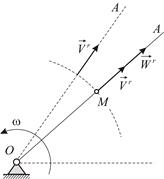
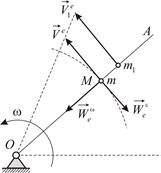
Как видно, абсолютное ускорение содержит несколько неожиданное слагаемое – ускорение Кориолиса. Поясним причину возникновения ускорения Кориолиса на простейшем примере. Пусть стержень вращается вокруг оси . Вдоль стержня движется точка .

Рис.3.2		Рис.3.3

Абсолютная производная от вектора относительной скорости характеризует изменение с течением времени вектора 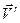по отношению к неподвижной системе координат. Вектор относительной скорости может изменяться в ходе относительного движения в силу кривизны относительной траектории или неравномерности относительного движения. Эти изменения учитывает вектор относительного ускорения. Но вектор относительного ускорения не может учесть поворот вектора 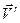, происходящий вместе с поворотом подвижного пространства (Рис. 3.2). Это изменение, наблюдаемое только из неподвижной системы отсчета, учитывает половина ускорение Кориолиса.

С другой стороны, абсолютная производная от вектора переносной скорости характеризует изменение с течением времени вектора 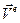по отношению к неподвижной системе координат. Вектор переносной скорости может изменяться в ходе переносного движения. Эти изменения учитываются ускорением точки 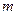, т.е. переносным ускорением. Но переносное ускорение не может учесть изменение переносной скорости, происходящее за счет относительного движения. 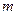Дело в том, что, совершая относительное движение, точка переходит из точки стержня в другую точку 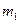, где переносная скорость уже другая (Рис. 3.3). Это изменение учитывает вторая половина ускорение Кориолиса.

Один из сомножителей ускорения Кориолиса 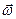– вектор угловой скорости подвижной системы отсчёта. Введение в рассмотрение вектора угловой скорости связано со многими обстоятельствами, важнейшее из которых – стремление использовать аппарат векторной алгебры для описания движения.

Вектор угловой скорости должен задавать положение оси вращения в пространстве. Для этого договоримся располагать этот вектор вдоль оси вращения. Чтобы по направлению вектора угловой скорости можно было судить о направлении вращения тела, будем направлять вектор угловой скорости так, чтобы с его конца вращение тела было бы видно происходящим против хода часовой стрелки. Итак,

вектор угловой скорости тела 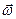расположен вдоль оси вращения и направлен в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки.

Как следует из определения (3.3), вектор ускорения Кориолиса перпендикулярен плоскости, содержащей вектор угловой скорости подвижной системы отсчета и вектор относительной скорости точки, причем направлен в ту сторону, откуда кратчайший поворот от вектора 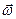к вектору 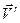виден против хода часовой стрелки (Рис. 3.4). Модуль ускорения Кориолиса определяется по формуле:

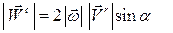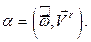где (4.4)

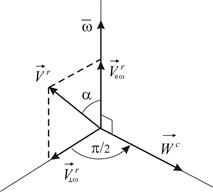Рис. 3.4		Рис. 3.5

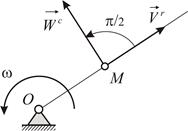
Правило Жуковского (Рис. 3.4):

для определения направления ускорения Кориолиса необходимо проекцию вектора относительной скорости на плоскость, перпендикулярную вектору угловой скорости подвижной системы отсчета, повернуть в сторону вращения на угол .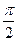

Особенно удобно применять правило Жуковского в тех часто встречающихся случаях, когда вектор относительной скорости перпендикулярен вектору угловой скорости подвижной системы отсчета (Рис. 3.5).

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что называется сложным движением точки?
2. Что называется относительной скоростью и относительным ускорением точки?
3. Что называется переносной скоростью и переносным ускорением точки?
4. В чём состоит теорема сложения скоростей?
5. В чём состоит теорема сложения ускорений?
6. Как вычисляется ускорение Кориолиса?
7. В чём состоит правило Жуковского?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1(9)

КИНЕМАТИКА ТОЧКИ

1.1. Координатный способ задания движения

Пример 1.1

Определить в интервале времени 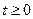траекторию точки шатуна 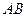кривошипно-шатунного механизма, если кривошип 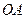вращается вокруг шарнира 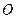так, что угол 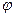изменяется по закону 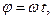где 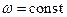(Рис.1.1). Дано: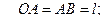

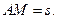
Вычислим координаты точки для произвольного положения механизма.

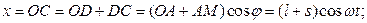
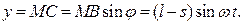
Для исключения параметра 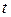воспользуемся основным тригонометрическим тождеством

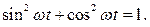
Возводя каждое из уравнений движения в квадрат

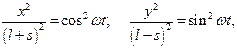
и складывая полученные уравнения, находим:

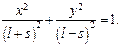
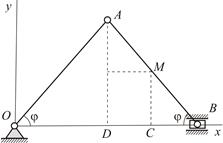Рис.1.1

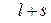Таким образом, точка движется по эллипсу с полуосями  и 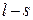 . При этом траекторией будет весь эллипс, поскольку он полностью укладывается в ограничения, получаемые из анализа кинематических уравнений движения: при 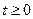имеем

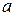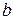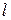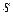Рассмотренный в этом примере кривошипно-шатунный механизм широко используется в технике для преобразования поступательного движения во вращательное и наоборот. Как видно, этот механизм можно также использовать в качестве чертежного инструмента для построения эллипсов с заданными полуосями и . Достаточно подобрать величины и так, чтобы выполнялись условия

Отсюда

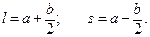
Пример 1.2

Снаряд движется в вертикальной плоскости. Угол наклона ствола орудия к горизонту 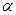. Начальная скорость снаряда 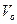. Определить траекторию снаряда, высоту и дальность обстрела, максимальную дальность обстрела. Сопротивлением воздуха пренебречь.

Заметим, что по условию задачи единственной силой, действующей на снаряд во время полета, является сила тяжести, которая сообщает снаряду ускорение свободного падения. Выбирая начало координат в точке расположения орудия и направляя ось 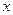горизонтально, а ось 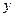вертикально (Рис.1.2), находим:

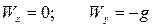или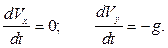

Получены обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными, интегрируя которые

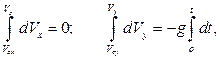
находим при заданных начальных условиях

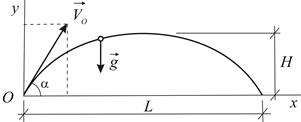Рис.1.2

законы изменения проекций скорости снаряда на координатные оси:

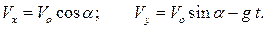(a)

Уравнения (a) можно рассматривать как дифференциальные уравнения относительно координат снаряда.

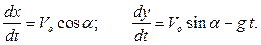
Выполняя интегрирование

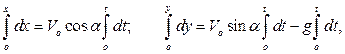
получаем закон движения снаряда:

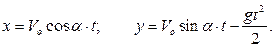(b)

Исключая время из уравнений (b) , получаем уравнение траектории снаряда:

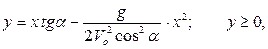
представляющей собой часть параболы, расположенную над осью .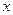

Обозначим 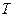время полета снаряда. Для момента падения снаряда имеем условия:

при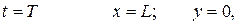

где 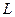– дальность полета снаряда. Подставляя эти условия в уравнения (b) , получаем

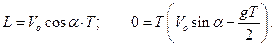
Отсюда

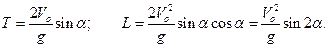
Очевидно, дальность будет максимальной, когда 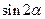принимает максимальное значение 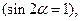т.е.

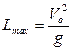при 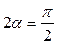, т.е. при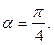

Для определения максимальной высоты 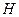снаряда воспользуемся тем, что в верхней точке траектории скорость горизонтальна. Обозначая 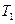время подъема снаряда на максимальную высоту, получаем

при .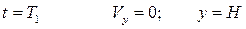

Из уравнений (a) , (b) имеем:

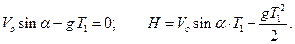
Отсюда

Пример 1.3

Движение точки задано уравнениями

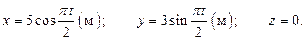
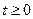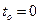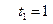Найти траекторию точки в интервале времени и определить положение точки, ее скорость и ускорение в моменты времени и с.

Находим траекторию точки. Исключая параметр 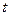из уравнений движения, получаем

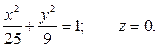
При 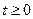имеем:

Таким образом, траекторией является эллипс с полуося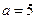ми м и 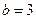м (Рис.1.3). Подставляя заданные моменты времени в уравнения движения точки, определяем ее координаты:

при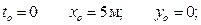

при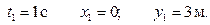

Вычисляем скорость точки:

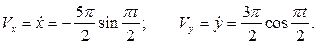
Подставляя в полученные формулы заданные моменты времени, находим:

при ,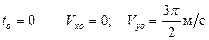

при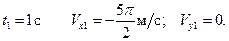

Вычисляем ускорение точки:

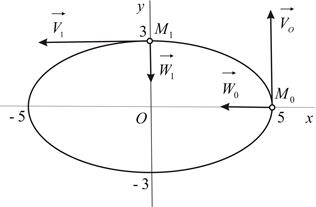Рис.1.3

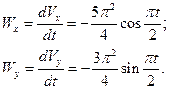
Подставляя в полученные формулы заданные моменты времени, находим:

при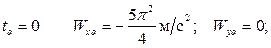

при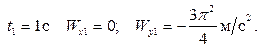

Результаты изображены на Рис.1.3.