Тема 4. Приложение производной.
Теорема Ферма. Если функция 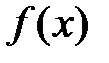 непрерывна на отрезке
непрерывна на отрезке 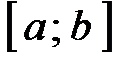 и достигает своего наибольшего или наименьшего значения во внутренней точке
и достигает своего наибольшего или наименьшего значения во внутренней точке 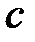 этого отрезка (т.е.
этого отрезка (т.е. 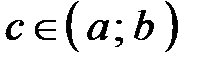 ), то, если в точке
), то, если в точке 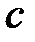 существует производная
существует производная 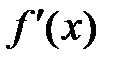 , то она обязательно равна 0:
, то она обязательно равна 0: 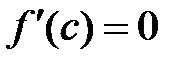 .
.
Геометрический смысл.
Касательная будет параллельна оси 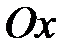 – геометрическое истолкование теоремы Ферма (Рис. 1).
– геометрическое истолкование теоремы Ферма (Рис. 1).
Теорема Ролля. Если функция 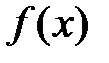 непрерывна на отрезке
непрерывна на отрезке 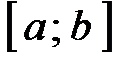 и дифференцируема на интервале
и дифференцируема на интервале 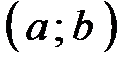 и при этом
и при этом 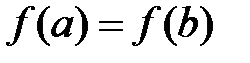 , т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка
, т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка 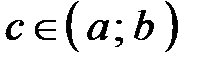 такая, что
такая, что 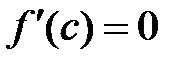 .
.
Геометрический смысл
Если на концах отрезка функция
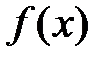
дифференцируема и принимает одинаковые значения, то найдется хотя бы одна точка, где касательная параллельна оси
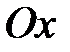
– геометрическое истолкование теоремы Ролля (Рис. 2).
Теорема Лагранжа. Пусть функция 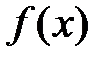 непрерывна на отрезке
непрерывна на отрезке 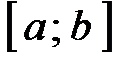 и дифференцируема на интервале
и дифференцируема на интервале 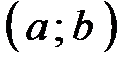 , тогда существует такая точка
, тогда существует такая точка 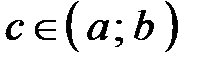 , что
, что
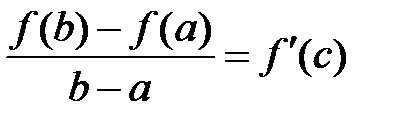 .
.
Геометрический смысл.
На отрезке 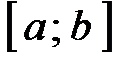 найдется хотя бы одна точка, в которой касательная к кривой
найдется хотя бы одна точка, в которой касательная к кривой 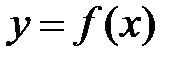 будет параллельна хорде, стягивающей концы дуги кривой (
будет параллельна хорде, стягивающей концы дуги кривой ( 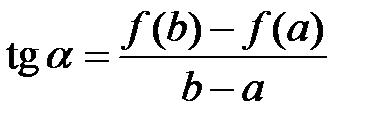 – тангенс угла наклона хорды, которая стягивает концы кривой) (Рис. 3).
– тангенс угла наклона хорды, которая стягивает концы кривой) (Рис. 3).
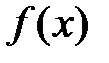 непрерывна на отрезке
непрерывна на отрезке 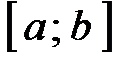 и достигает своего наибольшего или наименьшего значения во внутренней точке
и достигает своего наибольшего или наименьшего значения во внутренней точке 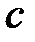 этого отрезка (т.е.
этого отрезка (т.е. 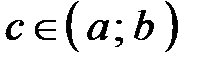 ), то, если в точке
), то, если в точке 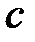 существует производная
существует производная 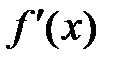 , то она обязательно равна 0:
, то она обязательно равна 0: 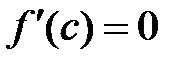 .
.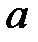
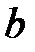
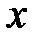
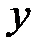
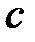
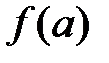
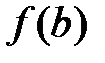
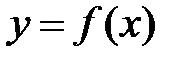

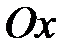 – геометрическое истолкование теоремы Ферма (Рис. 1).
– геометрическое истолкование теоремы Ферма (Рис. 1).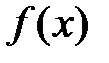 непрерывна на отрезке
непрерывна на отрезке 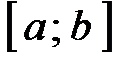 и дифференцируема на интервале
и дифференцируема на интервале 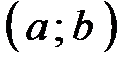 и при этом
и при этом 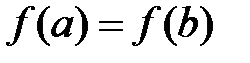 , т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка
, т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка 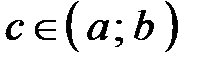 такая, что
такая, что 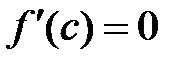 .
.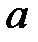
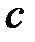
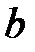
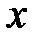
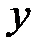

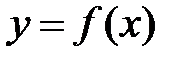
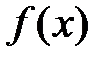 дифференцируема и принимает одинаковые значения, то найдется хотя бы одна точка, где касательная параллельна оси
дифференцируема и принимает одинаковые значения, то найдется хотя бы одна точка, где касательная параллельна оси 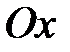 – геометрическое истолкование теоремы Ролля (Рис. 2).
– геометрическое истолкование теоремы Ролля (Рис. 2). 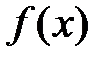 непрерывна на отрезке
непрерывна на отрезке 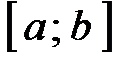 и дифференцируема на интервале
и дифференцируема на интервале 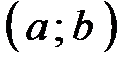 , тогда существует такая точка
, тогда существует такая точка 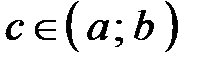 , что
, что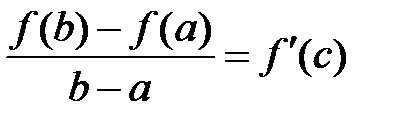 .
.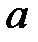
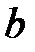
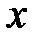
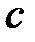
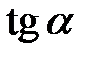
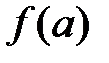
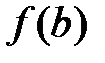
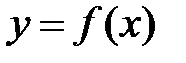

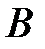
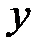
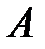
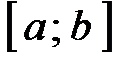 найдется хотя бы одна точка, в которой касательная к кривой
найдется хотя бы одна точка, в которой касательная к кривой 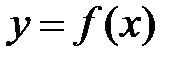 будет параллельна хорде, стягивающей концы дуги кривой (
будет параллельна хорде, стягивающей концы дуги кривой ( 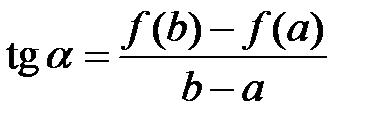 – тангенс угла наклона хорды, которая стягивает концы кривой) (Рис. 3).
– тангенс угла наклона хорды, которая стягивает концы кривой) (Рис. 3).