Определение вязкости и определение молекулярных параметров воздуха

Цель работы

Целью работы является ознакомление с явлением вязкости в газах и с методикой определения молекулярных параметров газов на основе измерения их вязкости (внутреннего трения).

Теоретические пояснения

Если в газе имеются соприкасающиеся слои, скорости движения которых различны, то из слоя газа с большой скоростью движения будет переноситься импульс (количество движения) к слою, движущемуся с меньшей скоростью, т.е. будет происходить выравнивание скоростей. Если внешними силами поддерживается постоянная разность скоростей движения различных слоев газа, то и поток импульса от слоя к слою будет стационарным. Он направлен вдоль направления падения скорости, а величина его для модели газа, движущегося в направлении Z, в котором измерение скорости происходит в направлении Х, определяется выражением:

L = -η (d /dх) (1)

где L – количество движения, переносимое за единицу времени через единичную площадь сечения, перпендикулярного к оси Х, d 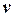/dх – градиент скорости. Коэффициент η (зависящий от свойств газа) называется коэффициентом вязкости или коэффициентом внутреннего трения. Изменение импульса слоя газа означает, что на него действует сила со стороны соседнего слоя и ее величина (на единицу площади соприкосновения слоев) равна L. Эта сила называется силой внутреннего трения

F_тр =- η (d 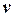/dх)dS (2)

Рассмотрим течение газа внутри горизонтальной цилиндрической трубы. Из опытов известно, что скорость течения слоев максимальна в центре трубы и уменьшается по мере приближения к ее стенкам. Скорость слоев, прилегающих к стенкам трубы, равна нулю (рис.1).

х

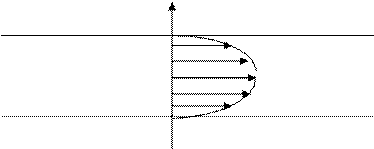Рис. 1. Зависимость скорости движения слоев газа от расстояния до центра трубы (показана длиной соответствующего вектора).

Рассмотрим движение газа вдоль трубы постоянного сечения радиусам R. Выделим мысленно слой газа, заключенный между цилиндрами, длина которых dZ, радиусы r и r + dr, а их оси совпадают с осью трубы (рис. 2).

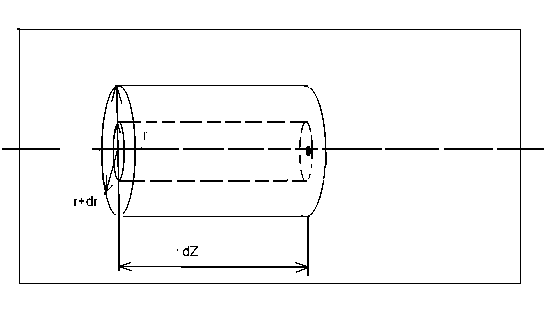
Рис. 2. Модель, используемая для вывода закона распределения скоростей в зависимости от радиуса трубы.

Составим уравнение движения такого слоя газа вдоль оси Z, если на него действует перепад давления (на торцах трубы).

На газ действуют:

1) сила внутреннего трения между слоями газа, движущимися с различными скоростями ( );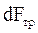

2) сила давления, возникающая из-за перепада давления на торцах трубы ( ).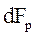

По второму закону Ньютона запишем:

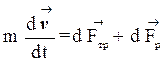(2)

где m – масса выделенного объема газа.

Так как поток стационарный, то (d /dt) =0. С учетом этого уравнение (2) станет:

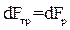
Здесь

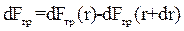
Или, с учетом (1):

d d

dF_тр = - η · 2πrdZ + η · 2π(r + dr)dZ,

dr r dr r+dr

где 2πrdZ и 2π(r + dr)dZ – площади боковых поверхностей цилиндрических слоев радиусов r и r + dr, соответственно.

Используя определение полного дифференциала функции:

df f(x+dx) – f(x)

=

dx dx

для 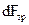можно записать:

d r d

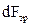= η2πdZ dr dr dr,

Для 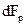= -dP·2πrdr, где 2πrdr = dS_п – площадь поперечного сечения трубы.

Итак, уравнение (2) можно переписать в виде:

d d

2π η dZ r dr = - dP·2πrdr

dr dr

или:

d d

ηdZ r = - dP·r

dr dr

Рассмотрим трубу конечной длины l с постоянным перепадом давления ΔР на ее концах. Заменим: dP = ΔР и dZ = l.

Тогда уравнение (3) станет:

ΔР 1 d d

- = η r

l r dr dr

Преобразуем его:

ΔР d

- rdr = d r

l η dr

Проинтегрируем это выражение и получим:

ΔРr² d

- = r + C

2l η dr

Умножим полученное выражение на (dr/r):

ΔРrdr dr

- = d + C

2l η r

И проинтегрируем:

ΔРr²

- = +C ln r + C₁

4l η

Отсюда получаем:

ΔРr²

(r) = - - C ln r - C₁ (4)

4l η

Для нахождения констант интегрирования С и С₁ дополняем это уравнение граничными условиями:

- при r = 0 скорость максимальна: (0) → max, следовательно, С = 0.

- при r = R (R) = 0, следовательно,

ΔРR²

С₁ = -

4l η

Итак, уравнение (4) станет следующим:

ΔРr² ΔРR²

(r) = +

4l η 4l η

Или, в окончательном виде:

ΔРR²

(r) = . 1 – r²/R²

4l η

Это выражение определяет скорость течения газа (или жидкости) как функцию расстояния от центра трубы.

Используя выражение (5), можно рассчитать объем газа V, протекающий за время Δt через сечение цилиндрической трубы радиуса R, длина которой l, если разность давлений на ее концах ΔР:

dV = dS_п · dh

Так как площадь поперечного сечения трубы S_п = πr² , то dS = 2πrdr.

Длина трубы dh может быть определена как путь, пройденный выделенным объемом газа за время Δt со скоростью (r): dh = (r) Δt.

Тогда объем газа определится выражением:

R

V = ∫ 2π·r·dr· (r)·Δt

Подставляя в это выражение формулу (5) для (r) и интегрируя, получаем:

π ΔР R⁴

V =Δt (6)

8l η

Полученная формула называется формулой Пуазейля. Она может быть использована для определения динамической вязкости η газа по измерению его объема, протекающего через капилляр в единицу времени.

Перенос импульса от одного слоя газа к другому происходит вследствие того, что между различными слоями имеет место обмен молекулами, обусловленный их тепловым движением. Поэтому динамическая вязкость определяется молекулярными параметрами газа: плотностью ρ, длиной свободного пробега λ и средней скоростью теплового движения молекул 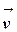. Это соотношение имеет вид:

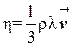, (7)

Где средняя скорость теплового движения равна:

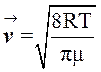(8)

μ – молекулярный вес газа.

Зная из опыта величину вязкости, а из (8) - среднюю скорость молекул данного газа, можно определить длину свободного пробега молекул λ. Последняя связана с числом молекул за единицу объема n и эффективным сечением молекулы σ = πd²/4 (d – диаметр молекулы) соотношением:

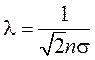. (10)

n с достаточной степенью точности можно принять равным числу Лошмидта

n_о = 2,7·10¹⁹ см^-3. Тогда диаметр молекулы воздуха (при условии, что молекулы имеют примерно равные размеры):

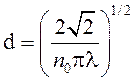(11)

Экспериментальная часть

Описание установки

Установка для определения вязкости воздуха и его молекулярных параметров изображена на рисунке 3.

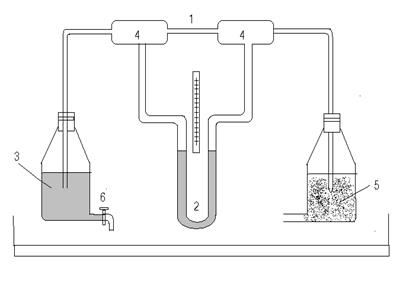
Рис. 3. Установка для определения вязкости воздуха и его молекулярных параметров: 1 – капилляр, 2 – водяной манометр, 3 – сосуд с краном (аспиратор), 4 – стеклянные трубки с расширением, 5 – сосуд с осушителем, 6 - кран.

Из сосуда 3 при открытом кране 6 вытекает вода и в нем создается разрежение. За счет перепада давления на концах капилляра через него протекает поток воздуха из атмосферы через сосуд с осушителем 5. При этом объем V воздуха, прошедший через капилляр за время Δt, равен объему вытекающей из аспиратора воды, если разность давлений ΔР, измеренная по манометру, остается неизменной (стационарное течение). Длина капилляра ℓ и его радиус R заданы. Объем V вытекающей воды измеряется по шкале на сосуде 3.