Формализм натуральных чисел

Человек обладает способностью образно различать количества предметов и представлять количественные образы в знаковой или символьной системе. Эта способность отражает свойство нашего интеллекта, а соответствующая символьная реализация называется натуральным рядом. Проанализируем процесс построения натурального ряда. Для этого вначале построим файл, определяющий эмпирические, то есть опытные, способности человека, на которых основана интересующая нас символьная формализация.

Ф.1.

Эмпирические свойства, предопределяющие структуру натурального ряда.

1о. Любой объект может быть выбран начальным элементом перечисления 2о. Для любого количества перечисленных элементов определено единственное следующее за ним количество 3о. начальному элементу не предшествует никакое количество 4о. Двум одинаковым количествам предшествуют два одинаковых количества 5о. Построенное множество количеств однозначно в том смысле, что все другие построенные таким образом количества совпадают и могут отличаться только символьными системами

Теперь займемся формализацией сформулированных свойств. Это означает, что требуется построить систему аксиом (правил), отражающих операции 1^о–5^о в символьной форме.

Дадим символьную реализацию операций 1^о–5^о. Свойство 1^о позволяет выбрать первый элемент, обозначим его 1. Свойство 2^о устанавливает операцию следования на множестве элементов. Эту операцию представим в виде схемы

(1)

… → x → s(x) → …

Заметим, что свойству 1 также удовлетворяет схема

… → x → s(x) → …

(2)

… → y

Свойство 4^о указывает, что схема (2) реализоваться не может. Свойство 3^о устанавливает первый элемент, и мы приходим к линейной цепочке

(3)

1 → s(1) → … → x → s(x) → …

Наконец, свойство 5^о утверждает, что всякая другая линейная цепочка со свойствами 1^о–4^о будет отличаться только знаковой системой

(4)

1 → a → … → b → g → …

Приведем в немного измененном виде систему аксиом Джузеппе Пеано (1858–1932), формализующую построение цепочки (3). При этом каждую аксиому сформулируем подробно и представим кратко на языке символов формальной логики.

Ф.2.	Структура натурального ряда
Множество, элементы которого удовлетворяют следующим свойствам 1о–5о, имеет структуру линейной цепочки (3) и называется натуральным рядом N
1о. Некоторый элемент называется первым и обозначается символом 1 $ x (x:= 1)
2о. Для всякого элемента x существует единственный элемент S(x), следующий за x "x $ y (y = S(x)) "x, y (y = x Þ S(x) = S(y))
3о. Единице не предшествует никакой элемент "x (S(x) ¹ 1)
4о. Всякому элементу предшествует единственный элемент "x, y (S(x) = S(y) Þ x=y)
5о. Аксиома индукции. Пусть подмножество ΜÌΝ содержит 1, и для его элементов x выполняются свойства 2о–4о (обозначим выполнение свойств 1о–4о T(x)). Тогда Ν Ì Μ
"x (xÎM)L(T(x)) Þ M=N

Заметим, что далеко не все свойства, “приписываемые” натуральному ряду, следуют из этой аксиоматики. Рассмотрим модель натурального ряда, предложенную норвежским математиком Торальфом Сколемом (1887–1963). К линейной цепочке (3) добавляются последовательности блоков вида

…→ a_–2 → α_–1 → α₀ → α₁ → a₂ → …

тогда в новой цепочке найдутся новые элементы, которые нельзя представить в виде конечного числа операций S. То есть некоторые элементы “y” модели Сколема не удовлетворяют условию

y = S (S (…S(1))),

где S (S (…S(1))) - конечное число композиций.

Такие элементы y назовем недостижимыми.

С другой стороны, в десятичной символьной модели натурального ряда
1, 2, 3, …, n, n+1, …, свойство конечной достижимости выполняется, так как десятичная запись содержит информацию о порядке числа. Десятичная система использует конечный цифровой алфавит 0, 1, 2, …, 9. Суть построения символа целого числа в этой системе в том, что вводятся операции сложения и умножения, и закон записи имеет вид "a Î N

a = a_na_n–1…a₁a₀= a_n˙10ⁿ + a_n–1˙10^n–1 + …+ a_1˙10 + a₀,

где a₀, a₁, …, a_nÎ(0, 1, …, 9)Ù(a_n ¹0).

Поскольку операции сложения и умножения ранее не фигурировали в модели Ф.2, то следует добавить аксиомы, определяющие свойства этих операций. Добавляя новые операции вместе с определяющими их аксиомами, мы не только расширяем свойства натурального ряда, но и само множество натуральных чисел. Рассмотрим этот процесс подробнее.

1.2. Операции, определяющие формирование
множества рациональных чисел

Практическая необходимость перечислять предметы привела к формированию понятия натурального ряда. Практическая же необходимость арифметических операций над натуральными числами приводит к формированию более широкого класса величин – рациональным числам. Схематично это выглядит так:

Натуральный ряд N	L	Операция сложения “+”; операция вычитания " – " обратная к сложению		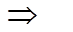Множество Z целых чисел (положительные, отрицательные и ноль)
Множество Z	L	Операция умножения “х”; обратная операция “:” деление.		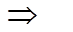Множество Q рациональных чисел вида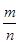

Схема 2

Вывод 1

Множество чисел представимых в виде несократимых дробей m/n, где: m, 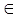n, N, n 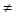0 называется множеством рациональных чисел и обозначается Q. На этом множестве определим операции ±, ´, :, и результат действия этих операций над рациональными числами есть снова рациональное число.

Мы не будем обсуждать все свойства рациональных чисел, а ограничимся напоминанием свойств систематического представления рациональных чисел, известных из элементарного курса математики.

Наличие операций сложения и умножения позволяет построить представление целых чисел при помощи алфавита, содержащего К знаков, называемых цифрами.

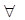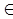Такое представление дается записью вида: aN

a = a_nKⁿ+... + a₁K+a_o(5)

и называется систематической К–ичной записью по основанию К. Символы a_o, a₁, ... , a_n принимают одно из К значений 0,1,2, ... , K–1. Если K 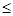10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2, ... , К–1. Для обозначения степеней оснований (классов) К¹, К², ..., Кⁿ используются уже введенные числовые обозначения (классы “тиражируются медленнее”, чем числа, входящие в эти классы).

Запись целых чисел в K–ичной системе позволяет реализовать арифметические операции над рациональными числами в виде некоторых алгоритмов, то есть правил выполнения последовательности простых операций над цифрами, представляющими рациональные числа.

В школьном курсе изучаются алгоритмы арифметических операций в десятичной системе.

Напомним для примера алгоритм сложения целых чисел.

Пусть а = 247 = 2 ^. 10² +4 ^. 10+7, в = 378 = 3 ^. 10² + 7 ^. 10 + 8

Найти С = а+в.

Складывая цифры, нумерующие разряды единиц, десятков и сотен, получаем:

7+8 = 10+5 (единицы)

4 ^.10 + 7 ^. 10 = 10²+10 (десятки)

2 ^. 10² + 3 ^. 10² = 5 ^. 10² (сотни)

Учитывая правила формирования разрядов, составляем десятичную запись числа С= а+в:

С = (10² +5 ^. 10²) + (10+10)+5 = 6 ^. 10² +2 ^. 10+5 = 625

Кроме реализации арифметических операций систематическое представление чисел дает алгоритм сравнения чисел по величине.

Для сравнения целых положительных чисел достаточно сравнить цифры разрядов по старшинству, например 197<211, так как 197<2^.10², а 211 > 2^.10².

Алгоритм представления рационального числа 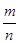в десятичной записи приводит к двум типам записи, известным из школьного курса.

Всякое рациональное число может быть представлено конечной десятичной дробью вида

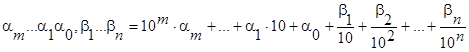, (6)

либо бесконечной периодической дробью вида:

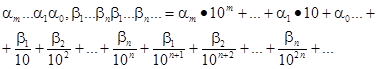
(7)

Напомним также, что алгоритм представления рационального числа в виде (6) или (7) основан на следующем свойстве целых чисел.

Для любых a, b 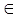N , (a > b) существуют m, n 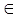N,(m<a, n<b) такие, что

а = bm+n (8)

Вывод 2

Аксиоматика рациональных чисел должна содержать правила, определяющие операции сложения, умножения, сравнения чисел и связь между этими операциями.

Замечание 1

Запись рациональных чисел в виде (7) требует обоснования, которое заключается в объяснении сходимости числового ряда, т.е. существования конечного числа, являющегося результатом бесконечного суммирования в следующей записи:

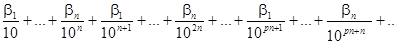(9)

Объяснение того, что эта сумма представляет конечное число, основано на формальных оценках

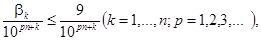
позволяющих показать, что сумма (9) не превосходит n сумм геометрических прогрессий: