Бір оқиғаның ақпараты

М. ӘУЕЗОВ АТЫНДАҒЫ ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

КОДТАУ НЕГІЗДЕРІ

М. ВЕРНЕР

ЖОҒАРҒЫ ОҚУ

ОРЫНДАРЫНА

АРНАЛҒАН ОҚУЛЫҚ

Азақша тәржімесі

Шымкент 2016

I ТАРАУ

АҚПАРАТ

ЖӘНЕ

КОДТАУ

I БӨЛІМ

КІРІСПЕ

Ақпараттар теориясы ықтималды кодтау диаграммасы көмегімен және ақпаратты нақты, табиғи-ғылыми бағдарламаларда тасымалдау арқылы сипатталады. Сонымен қатар техникалық системалардағы ақпараттар ағынын талдауға және үйлесімділеуге мүмкіндік пайда болады. Ақпараттың техникалық көрінісін тұрмыстықтан айыру үшін лингвистикалық түсініктер жәрдемдесуі мүмкін: синтаксис, семантика және прагматика. Бұл түсініктерде синтаксис және семантика техникалық мағлұматтардың аналогы болып табылады. Синтаксис барлық мүмкін символдарды және символдар реттілігін анықтайды. Семантика олардың мәнін түсіндіреді. Дәл мағынасын және қолдану саласы прагматикамен түсіндіріледі. Прагматика мағлұмат, техникалық ақпарат және ақпарат сөзінің тұрмыстық түсінігін біріктіреді. Әдетте әрекетке үндеу немесе нұсқау ретінде түсінілетін “ақпарат” термині жеткізілуге міндетті хабарламаға айналады.

• Синтаксис + семантика ⟶ Мағлұмат.

• Мағлұмат + прагматика ⟶ Хабарлама.

Алдағы талқылаулардың негізі ақпараттың қандай-да бір тәжірибемен орнатылатын шама ретінде түсінілуі болып табылады. Бұған 1948 жылы жарияланған Клод Шеннонның “Математикалық байланыс теориясы” атты еңбегі түрткі болды. Онда К. Шеннон заманауи ақпараттар теориясы түсінігіне анықтама берді және бүгінгі байланыс техникаларының негізін салды. Шеннон, мысал ретінде, сол уақытта кең таралған перфокарталарды келтірді. Тесік үшін арналған N мүмкін позициялы перфокартада нақты 2^N хабарлама болады. Егер екі перфокарта болса, онда мүмкіндіктер саны 2^2N-ге тең болады. Осылайша, екі перфокарта алып жүрген мүмкін хабарламалардың саны бір перфокартадағы хабарламалар санының квадратына тең. Сонымен қатар екі перфокарта бір перфокартаға қарағанда екі есе артық ақпарат сақтай алатынын жорамалдауға болатын еді. Мұнда ақпарат өлшемін сипаттау үшін келесі еселікті беретін логарифмдық функция сұратылады:

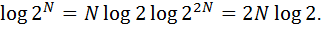
Шеннонның жалпы байланыс үлгісі 1.1 суретте көрсетілген

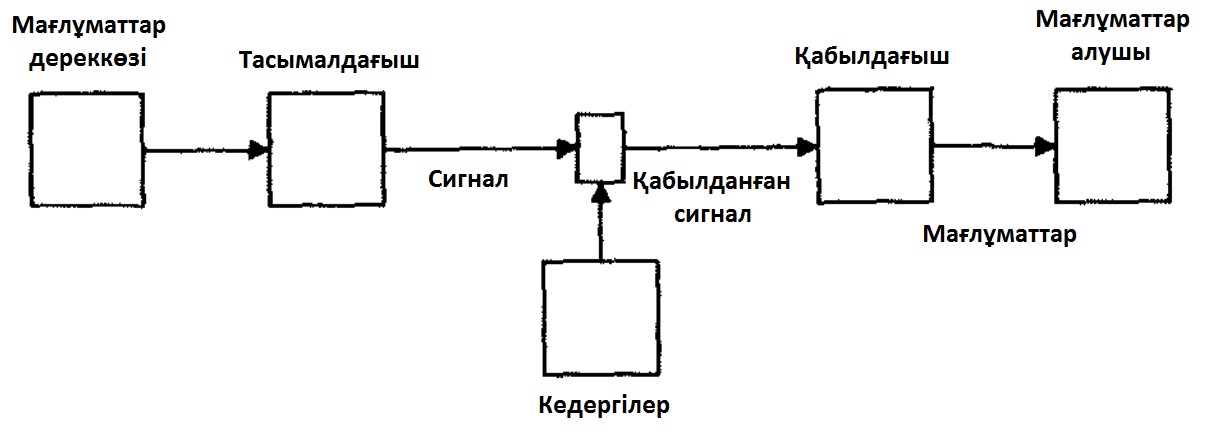
1.1 Сурет. К. Шеннон бойынша байланыс каналы арқылы ақпарат тасымалдау үлгісі.

Ақпарат дереккөзі бастапқы нүкте болып табылады. Оның хабарламала-ры тасымалдағышқа жіберіледі. Сонымен қатар, хабарламалар өзімен байланысты мәтіннің жеке әріптерін, уақыт функцияларының мәнін, микрофон шығысындағы кернеудің өзгеру функцияларын, телевизионды сигналдарды және т.б. функцияларды ұсынуы мүмкін. Тасымалдағыш каналдың физикалық қасиеттеріне сәйкес сигналдарды өңдейді. Канал суретте тасымалданып жатқан сигналға біршама ықпал ететін кедергінің қайнар көзі ретінде көрсетілген. Шулы сигнал ең ауыр міндеттер жүктелген қабылдағышқа түседі. Ол шулы сигналдан жіберілген хабарламаны бөліп алып пайдаланушыға жіберуі қажет.

Бұл кітаптің екінші бір үлкен тақырыбы – кодтау. Кодтау сөзін біршама хабарламаны мағлұм қағидаттарға сәйкес көрсету деп түсінеміз. Сонымен қатар ақпарат тасымалдаудың шеннондық үлгісінде тасымалдағыштың және қабылдағыштың блоктарын осы қағидаларға сәйкес кеңейту қажет. Дереккөздерді кодтау мен каналдарды кодтау арасында айқын айырмашылық бар. Дереккөздерді кодтаудың мысалы байланысқан мәтінді Морзе коды арқылы тасымалдау, аудио сигналды компакт дискіге жазу барысындағы цифрлеу болып табылады. Дереккөздерді кодтау уақтысында хабарламалар шығыны төмендейді және мұндай кодтауды жиі мағлұматтарды қысу деп атайды. Каналдарды кодтау, керісінше, хабарламалар шығынын жоғарылатады. Қосымша тексеру символдарын енгізу канал арқылы ақпарат тасымалдау уақтысында пайда болатын қателерді табуға және түзетуге мүмкіндік береді. Мұнан былай каналды кодтауды біз кедергіге төзімді кодтау деп атаймыз. Кедергіге төзімді кодтаусыз CD-ROM, DVD немесе қатты диск секілді ұлкен сыйымдылықты

жинақтаушыларды жасау мүмкін емес болатын. Кедергіге төзімді кодтауға жазу/оқу уақтысындағы жарамды ықтималдықтарды қамтамасыз ететін қосымша шығын жазу тығыздығында жеткен ұтыспен салыстырғанда өте аз болып қалады. Қарап шығылған мысалдар ақпарат және кодтау заманауи ақпараттық техникалардың негізі болған басты түсініктер болып табылатынын көрсетеді. Келесі бөлімдер бұл түсініктерді және олардың қолданылуын тереңдетеді.

БӨЛІМ

АҚПАРАТ,

ЭНТРОПИЯ ЖӘНЕ

ШЫҒЫН

Бір оқиғаның ақпараты

Ақпарат алмасу, өзінің материалды емес табиғатына қарамастан, біздің өміріміздің ажыралмас бөлігі болып табылады. Заманауи ақпараттар теориясының негізін қалаушылардың бірі, Норберт Виннер, ақпаратты келесі түрде сипаттады [9]:

“Ақпарат ол матерал да емес, энергия да емес, ақпарат ол ақпарат”.

Н. Виннердің пікірінше, ақпарат ол материя және энергия секілді жаңа бір элемент. Ақпарат түсінігі ғылыми түрде қаншалықты күрделі болса, адамзат үшін ақпарат соншалықты маңызды. Біз қандай-да бір дербес оқиғаны мысалға ала отырып: “Бұл мағлұматтың мен үшін маңызы зор” - деп айтамыз. Мұндай субъективті көзқарас ақпараттың техникалық сипаттамасына тура келмейді.

Қатаң ғылыми түсінік болғандықтан, ақпарат техникаға өлшенетін шама ретінде енгізілуі қажет(ұзындықтағы метрге, кернеудегі вольтқа ұқсас).

Біздің күнделікті тәжірибеміз ақпаратты қабылдаған уақытта біз әрдайым қандай-да бір белгісіздікті айқындайтынымызды көрсетеді. Бұл кездейсоқ оқиғалармен тәжірибені еске түсіреді. Мұндай тәжірибелерді өткізіп біз кездейсоқ оқиғаларды бақылаймыз және бұл жүйенің беймағлұмдығын төмендетеді.

Енді ақпараттық теорияның өзіндік мазмұнына өтеміз. Әуелі, қарапайым дереккөздің сипаттамасын берейік, онан соң оның жәрдемімен дереккөзді суреттеу үшін өлшенетін шама ретінде ақпарат саны түсінігін енгіземіз.

Жадсыз дискретті дереккөз

Жәй Х жадсыз дискретті дереккөзі уақыттың әр назар салынған сәтінде

P(x_i) = p_i ықтималдықпен P(x_i) = {х₁, х₂, ... , х_N} ақырғы алфавитінен х_і символын береді. Символ талғау бір бірінен тәуелсіз мәртебеде өтеді.

Қарапайым мысал ретінде Х = {x₁ = 0, x₂ = 1} алфавитті және 0 ≤ р₁ ≤ 1 һәм р₂ = 1 – p₁ ықтималдықты екілік жадсыз дереккөзді келтіруге болады. Келесі сан талғауы бастапқы немесе соңғы таңдаулардан тәуелсіз түрде өтеді. Қарапайым дереккөздің бейнесі 2.1 суретте көрсетілген. Әуелі біріңғай оқиғаларды қарастырайық. Күнделікті тәжірибеміздің нәтижесі жиі орын алатын оқиғалар және олардың ықтималдықтары бізге аз мағлұмат беретінін көрсетеді. Мысал үшін “Ит иесін тістеп алды” деген хабарламаны алайық. Бұл үйреншікті жағдайды барлық газеттер үлкен шрифтпен жазса да оған ешкім назар аудармас еді. Бұдан келесі қорытынды шығаруға болады: жиі болатын оқиғалар өзімен аз мағлұмат алып жүреді және керісінше сирек яғни күтілмеген оқиғаларда көп мағлұмат болады. Демек ақпарат және ықтималдық бір-біріне теріс пропорционалды түрде тәуелді. Мұнан шыға, келесі үш аксиома негізінде өлшенетін шама ретінде ақпарат саны деген түсінік енгіземіз [1].

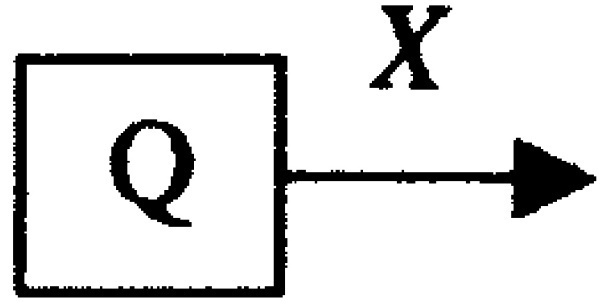
2.1 Сурет.Қарапайым Х алфавитінің ақпарат дереккөзі.

Ақпарат санын анықтауға арналған аксиомалар [1]

1. Жалғыз x₁ Є X оқиғасының р_і ықтималдығымен болған ақпараты оң мәнге ие

2. Екі тәуелсіз (x_i , x_j) оқиғаларының бірлескен ақпараты бірлескен P(x_i, х_j) = р_ij = р_i ∙ р_j ықтималдығымен олардық ақпараттарының қосындысына тең

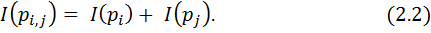
3. Ақпарат оқиға ықтималдығынан үзілмес функция болып табылады.

1 және 2 аксиомалардың тұжырымдамасы бірнеше оқиғаның ақпараты өзара жойыла алмайтындығын көрсетеді. 2 аксиома оқиғаның бірлескен ақпараты түсінігін енгізеді. 3 аксиоманың бойынша оқиға ықтималдығындағы өзгеріс оның мағлұматының да өзгеруіне әкеліп соғады. 2 аксиома екі тәуелсіз оқиғаның ақпаратын анықтайды. Оқиға ақпараты оның ықтималдығының логарифмдік функциясы ретінде анықталатынын (2.2) білеміз. Демек, ақпаратты келесі жолмен анықтай аламыз:

Р ықтималдықпен болып жатқан оқиғаның ақпараты, тең болады

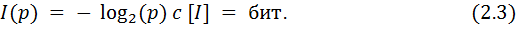
Бұл формулада екілік логарифм қолданылған. Екілік логарифм келесі сипаттарда да берілуі ықтимал: log₂(x) = ld (x) = lb(x) , ld дегені дуальды лоагрифм термині, lb – бинарлы. Кейде нат бірлік шамалы натуралды логарифмді қолданады, бірақ ақпараттың кез-келген өлшем бірлігін де қолдануға болады. Сонымен қатар есептеу формуласын қолданып бір бірліктен екіншісіне өтуге де мүмкіндік бар:

.

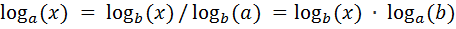Бит өлшемі ақпараттық техникада екілік есептеу системасында қолданылады. Келесі тарауларда суреттелетіндей, кез-келген сұраққа екі ғана жауабы бар шешім қабылдау процессін сипаттауда екілік система өте қолайлы: “иә” және “жоқ”. “Бит” түсінігінің көрнекі интерпретациясы [10]-да көрсетілген.

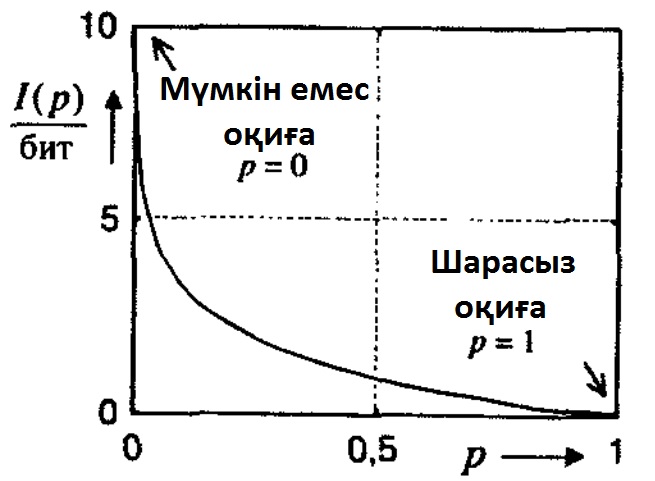
2.2 Сурет.I(p) символының ақпараты р пайда болу ықтималдығымен.

2.2 суретте ақпараттың ықтималдық функциясы туріндегі қызметі. Әрдайым болып жатқан оқиғаның ақпараты 0-ге тең. Белгісіздігінің өсуімен ақпарат мүмкін емес оқиғаның шексіздікке ұмтылуы үшін де өседі. Сөйтіп, ақпарат алдын ала келтірілген барлық талқылауларларға сәйкес және 1 – 3 аксиомаларын да қанағаттандырады.

Ықтималдықтар теориясының тұрғысынан алғанда, ақпарат анықтауды оқиғаның біршама бейнесі деп қарастыруға болады. Ұқсас кескіндер стохастикалық айнымалыларға ие. Келесі тарауларда бұл мысалдар түрінде қарастырылады.