ЛЕКЦИЯ № 25. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Вопрос 25.1. Метод Рунге-Кутта.

Пусть 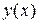есть точное решение задачи Коши. Если 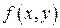имеет непрерывные производные вплоть до n-го порядка включительно, то 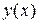имеет производные до n+1 до порядка, поэтому по формуле Тейлора получим

.

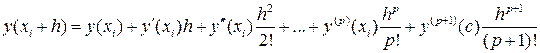Тогда при малых значениях h имеем приближенную формулу:

.

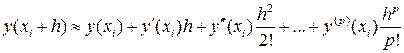Эту формулу можно положить в основу численного метода

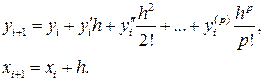(1)

где

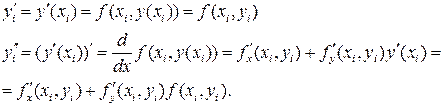
и т.д.

Метод (3) называют методом p-го порядка. Чем выше порядок метода, тем он точнее и можно брать более крупный шаг h. Метод Эйлера имеет порядок 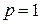, он самый простейший и поэтому его точность часто недостаточно велика, и необходимо использовать методы более высоких порядков или брать очень маленькие величины h. С ростом p вычисление производных быстро усложняется и метод (1) поэтому не находит применения при значениях 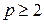. Вместо этого метода, Рунге и Кутт предложили другой метод, наиболее распространенный в наше время. Если в i-м узле 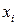известно, то решение в этом узле берут в виде

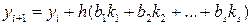(2)

где

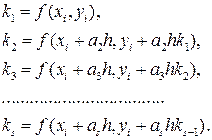
Параметры выбирают так, чтобы метод имел требуемый порядок p, то есть, чтобы при разложении (2) по степеням h это разложение совпадало с (1) до степени включительно.

Пример 25.1. Метод Рунге-Кутта 2-го порядка.

Требуется получить семейство методов 2-го порядка. Пусть

Разложим 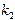по формуле Тейлора до слагаемых порядка h

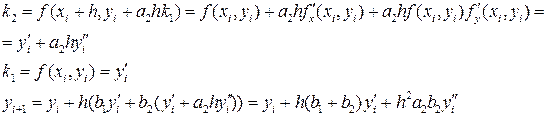
Отсюда, чтобы получить метод второго порядка, необходимо выполнение равенств

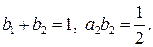
Тогда получим

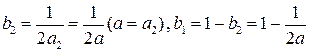
Тогда получаем семейство методов Рунге-Кутта 2-го порядка

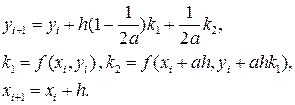
Наиболее часто используется схема предиктор-корректор a=1

а так же усовершенствованный метод Эйлера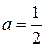

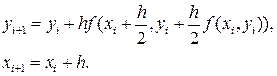
Конец примера.

Наиболее часто используется метод Рунге - Кутта 4-го порядка

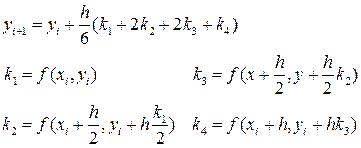
Для оценки погрешности разностного метода существует эмпирическое правило Рунге:

Если - решение, полученное на сетке с шагом h, а 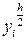- решение, полученное на сетке с шагом 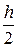, то в общих узлах погрешность вычислений приближенно равна

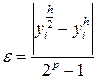, где p порядок метода.

Составим таблицу:

Метод Эйлера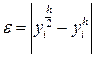

Метод Рунге - Кутта второго порядка .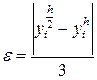

Метод Рунге - Кутта четвертого порядка .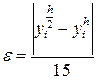

Полученное решение можно уточнить по формуле Ричардсона

,

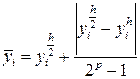повысив порядок метода еще на единицу.

Пример 25.2. Найти численное решение задачи Коши методом Рунге-Кутта второго порядка (схема предиктор - корректор)

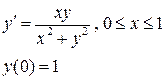
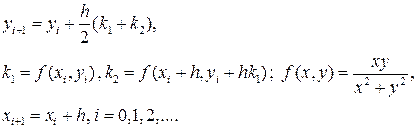
Пусть h = 0.25, результаты расчетов приведем в таблице

Таблица 1.

i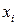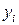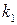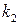
	0.0			0.23529
	0.25	1.02941	0.22933	0.37971
	0.5	1.10554	0.37547	0.44954
	0.75	1.20867	0.44801	0.48126
	1.0	1.32483

Пусть h = 0.125, результаты расчетов приведем в таблице

Таблица 2. ( 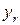‑ уточнение по Ричардсону)

I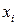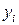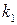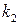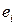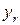
	0.0			0.12308
	0.125	1.00769	0.12217	0.23061
	0.25	1.02974	0.22927	0.31479	0.00011	1.02985
	0.375	1.06374	0.31356	0.37605
	0.5	1.10685	0.37517	0.41881	0.00043	1.10728
	0.625	1.15647	0.41827	0.44800
	0.75	1.21061	0.44769	0.46765	0.00065	1.21126
	0.875	1.26782	0.46749	0.58482
	1.0	1.33359			0.00292	1.33651

Конец примера.