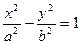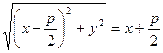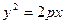Условия параллельности и перпендикулярности двух прямых
|
 Bυ7 = 0 :k2 – k1 = 0 => .
Bυ7 = 0 :k2 – k1 = 0 => . Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.
|
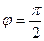 , то из (1) находим ctg φ2
, то из (1) находим ctg φ2 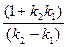 . В этом случае
. В этом случае 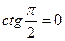 и 1 + k2k1 = 0 => .
и 1 + k2k1 = 0 => . Таким образом, условия перпендикулярности двух прямых состоит в том ,что их k обратны по величине и противоположны по знаку.
Взаимное расположение двух прямых на плоскости.
Пусть прямые L1 и L2 заданы уравнениями: 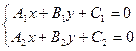 (10)
(10)
Решая эту систему, найдем: 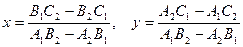 .
.
Пусть A1B2 – A2B1 ≠ 0, тогда найденные формулы дают решение системы (10). Это значит, что L1 не параллельна L2, L1 ∩ L2 = точке (x; y). Пусть теперь A1B2 – A2B1 ≠ 0. Возможны два случая:1) A2C1 – A1C2 = 0 и B1C2 – B2C1 = 0;
2) A2C1 – A1C2 ≠ 0 (B1C2 – B2C1 ≠ 0).
В первом случае имеем А2 = МА1, В2 = МВ1, С2 = МС1 или 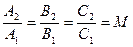 , где
, где
М≠ 0 - некоторое число. Это означает ,что коэффициенты уравнений пропорциональны следовательно второе уравнение получается из первого умножением на число М. В этом случае L1 и L2 совпадают, т.е. уравнения определяют одну и ту же прямую.
Во втором случае, если, например, A2C1 – A1C2 ≠ 0, то допустив, что система имеет решение (х0; у0), получим противоречие A2C1 – A1C2 = 0, что противоречит предположению. Таким образом, система (10) решения не имеет. В этом случае прямые L1 и L2 не имеют точек пересечения, т.е. они параллельны.
Итак, две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.
Расстояние от точки до прямой.
Теорема. Расстояние α от данной точки М (х0; у0) до прямой L, заданной уравнением
|
(11)
Рассмотрим на прямой L две " точки E и F c координатами (х1; у1) и (х2; у2).
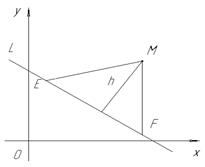
Вычислим длину отрезка EF и S MEF. Тогда 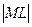 - это длина высоты h rMEF.
- это длина высоты h rMEF. 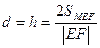 .
.
Доказательство.
|
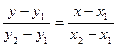 => (12)
=> (12) SrMEF запишем по формуле (3) из Bυ3 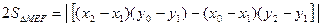
|
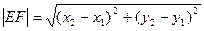
(13)
С помощью уравнения (12) выразим теперь коэффициенты А, В, С уравнения
Ах + Ву + С = 0 прямой L через координаты точек E и F. Для этого перепишем уравнение (12) в виде 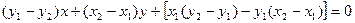 =>
=>
=> 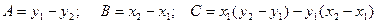 . Тогда
. Тогда 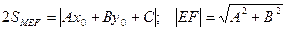 .
.
Формулу (13) можно переписать в виде 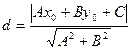 .
.
11. Линии второго порядка:
- общее уравнение линий второго порядка;
|
(1)
А, В, С одновременно не равны нулю.
- инвариантность выражения АС – В2;
Начнем с исследования пересечения линии второго порядка с произвольной прямой, заданной при помощи параметрических уравнений
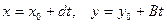 (2)
(2)
Значение t, соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой (2) в (1): 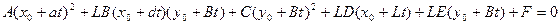 .
.
|
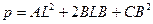 . Полученное уравнение является квадратным, но для некоторых прямых может оказаться линейным. Это произойдет , если p = 0 , т.е., если
. Полученное уравнение является квадратным, но для некоторых прямых может оказаться линейным. Это произойдет , если p = 0 , т.е., если
|
(4).
Это соотношение останется справедливым, если умножим L и В на ненулевой множитель, т.е. возьмем другой направляющий вектор прямой.
Определение. Направление, определяемое вектором, компоненты которого удовлетворяют уравнению (4), называется асимптотическим направлением линии второго порядка. (1).
|
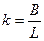 , то k должен удовлетворять уравнению (5).
, то k должен удовлетворять уравнению (5). При С ≠ 0 это уравнение имеет два корня, если 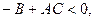 1, если
1, если 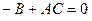 и ни одного вещественного корня, если
и ни одного вещественного корня, если 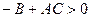 .
.
Обозначим буквой b детерминант
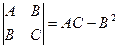
При С = 0 очевидно, что b = - B2.
Предложение. Линия второго порядка имеет два асимптотических направления, если
b < 0, одно, если b = 0, и ни одного, если b > 0. Следовательно знак детерминанта b не зависит от выбора декартовой системы координат, т.е. является инвариантом.
- определение типа линии, классификация линий второго порядка;
Определение. Линия второго порядка называется линией гиперболического, параболического или эллиптического типа, смотря по тому, имеет ли она два, один или ни одного асимптотического направления.
Инвариантным признаком типа линии является знак детерминанта b.
Лини эллиптического и гиперболического типов объединяются под общим названием центральных линий второго порядка. Центральные линии имеют единственный центр симметрии.
- эллипс, определение и вывод канонического уравнения;
Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Для вывода уравнения эллипса введем на плоскости прямоугольную систему координат так, чтобы фокусы эллипса лежали на оси Ох, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение эллипса в выбранной системе координат.
Обозначим фокусы эллипса через F1 и F2 . Пусть М – произвольная точка эллипса. 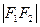 обозначим через 2с, сумма расстояний от точки М до фокусов – через 2а.
обозначим через 2с, сумма расстояний от точки М до фокусов – через 2а.
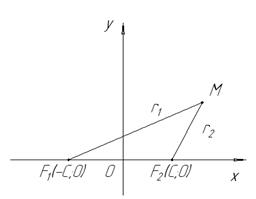
Так как по определению 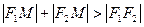 , то 2а > 2с или а > c. Обозначим через r1 и r2 расстояние от точки М до F1 и F2. Числа r1 и r2 называются фокальными радиусами точки М. Из определения следует, что точка М (х; у) С на данном эллипсе в том и только в том случае, когда
, то 2а > 2с или а > c. Обозначим через r1 и r2 расстояние от точки М до F1 и F2. Числа r1 и r2 называются фокальными радиусами точки М. Из определения следует, что точка М (х; у) С на данном эллипсе в том и только в том случае, когда
r1 + r2 = 2 a (6).
Чтобы получить искомое уравнение эллипса, нужно в равенстве (6) заменить переменные r1 и r2 их выражениями через координаты х и у.
Так как F1 и F2 расположены на оси Ох симметрично относительно (0; 0), то F1(-C;0), F2(C; 0). Применяя формулу (1) Bυ2, находим 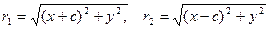 (7)
(7)
Подставим (7) в (6):
|
(8) –
искомое уравнение эллипса. Это уравнение обычно приводят к более простому виду. Для этого перенесем второй корень (3) в правую часть уравнения, а затем возведем обе части равенства в квадрат: 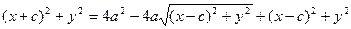 .
.
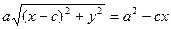 (9)
(9)
Снова возведем обе части равенства в квадрат: 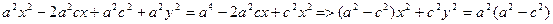 (10)
(10)
Введем новую величину: 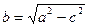 (11)
(11)
Так как по условию a > c, то 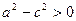 и, следовательно b > 0. Из равенства (11) имеем
и, следовательно b > 0. Из равенства (11) имеем 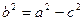 , поэтому уравнение (10) можно записать в идее:
, поэтому уравнение (10) можно записать в идее:
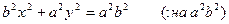
|
(12) – коническое (простейшей) уравнение эллипса.
Убедимся в том, что уравнение (8) и (12) равносильны. Для этого достаточно показать, что величины r1 и r2 для " точки, координаты которой удовлетворяют (12), удовлетворяют (6). Пусть координаты " точки удовлетворяют уравнению (12) (х; у). Тогда, подставляя в выражение (7) для r1 значение 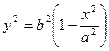 (из (12)),
(из (12)), 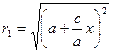 . Так как
. Так как 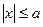 (из (12)) и
(из (12)) и 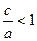 , то
, то 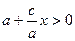 и поэтому
и поэтому 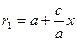 . Аналогично,
. Аналогично, 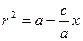 . Складывая почленно эти равенства, получаем соотношение (6). Т.о. (12) – уравнение эллипса.
. Складывая почленно эти равенства, получаем соотношение (6). Т.о. (12) – уравнение эллипса.
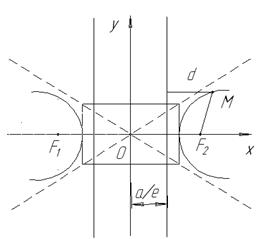
- гипербола, определение и вывод канонического уравнения;
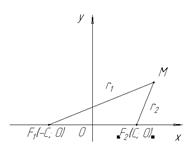
Определение.Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстоянию между фокусами. Для вывода уравнения гиперболы введем на плоскости прямоугольную систему координат ток чтобы F1C Ox и F2COx и
|
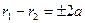 (13)
(13)
Чтобы получить искомое уравнение гиперболы, нужно в (13) заменить r1 и r2 их выражениями через координаты x и у. F1 (-C; 0), F2 (C; 0).
По формуле (1) Bυ2находим:
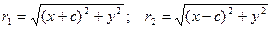 (14)
(14)
Подставляя эти выражения в равенство (9), получаем:
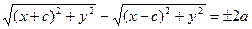 (15) –
(15) –
искомое уравнение гиперболы. Перенесем второй корень в правую часть уравнения, а затем возведем обе части в квадрат: 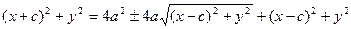
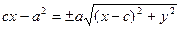 (16)
(16)
Снова возведем обе части уравнения в квадрат: 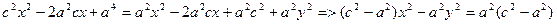 (17)
(17)
Введем новую величину 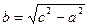 (18).
(18).
Так как с > a, то 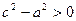 и b > 0. Из (18) имеем
и b > 0. Из (18) имеем 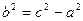 . Уравнение (17) примет вид
. Уравнение (17) примет вид 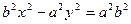 или
или
|
(19) - коническое уравнение гиперболы.
- парабола, определение и вывод канонического вида;
Определение.Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
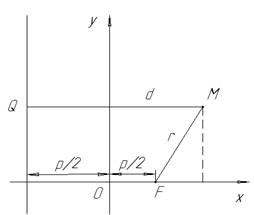
Для вывода уравнения параболы введем на плоскости прямоугольную систему координат так, чтобы Ох проходила через F перпендикулярно директрисе, и будем считать положительным направлением направление от директрисы к фокусу; начало координат расположим посередине между F и директрисой.
Пусть М (х; у) – произвольная точка параболы. Обозначим 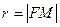 , через d - расстояние от М до директрисы, а через p – расстояние от F до директрисы. Величину p называют параметром параболы. Т. М будет С на данной параболе в том случае когда
, через d - расстояние от М до директрисы, а через p – расстояние от F до директрисы. Величину p называют параметром параболы. Т. М будет С на данной параболе в том случае когда
r = d (20)
Чтобы получить искомое уравнение, нужно в (20) заменить переменные r и d их выражениями через координаты х и у. 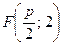 ; поэтому по формуле (1) Bυ2находим:
; поэтому по формуле (1) Bυ2находим:
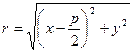 (21).
(21).
Обозначим через Q основание перпендикуляра, опущенного из M на директрису 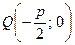 следовательно и из (1) Bυ2 получаем:
следовательно и из (1) Bυ2 получаем:
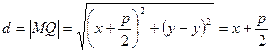 (22).
(22).
|
- искомое уравнение параболы (23).
Обе части равенства (23) возведем в квадрат: 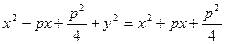 или
или
|
- каноническое уравнение параболы (24).
Проверим, что (24) после возведения в квадрат обеих частей равенства (23) не приобрело «лишних» корней. Для этого достаточно показать, что для любой точки, координаты х и у которой удовлетворяют уравнению (24), выполнено соотношение (20). Действительно, из уравнения (24) следует, что 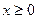 , поэтому для точек с неотрицательными абсциссами
, поэтому для точек с неотрицательными абсциссами  . Подставляя значение у2 из (24) в (21) для r и учитывая, что
. Подставляя значение у2 из (24) в (21) для r и учитывая, что 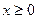 , получаем, что
, получаем, что 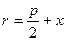 , т.е. r = d, что и требовалось доказать.
, т.е. r = d, что и требовалось доказать.

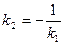
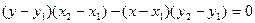
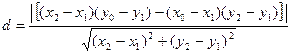
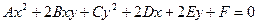
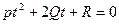
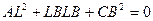
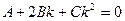
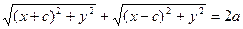
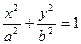
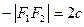
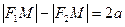 . Так как, по определению,
. Так как, по определению, 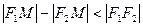 , то 2а < 2с или а < c. Числа
, то 2а < 2с или а < c. Числа 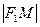 и
и 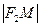 называются фокальными радиусами т.М и обозначаются через r1 и r2. Из определения следует, что т. М(х; у) С на данной гиперболе в том и только в том случае, когда
называются фокальными радиусами т.М и обозначаются через r1 и r2. Из определения следует, что т. М(х; у) С на данной гиперболе в том и только в том случае, когда 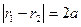 следовательно
следовательно