Прямая и плоскость в пространстве
1. Уравнение плоскости:
-- перпендикулярной данному вектору n=(А,В,С) и проходящей через данную точку М0(х0,у0,z0)
А (х-х0)+В (у-у0)+С (z –z0)
-- в отрезках х/а+у/b+z/c=1
-- общее Ах+Вх+Сz+D=0.
2. Даны две плоскости А1х + В1у + С1z + D1 = 0 (1) и А2х+ В2у + С2z + D2 = 0 (2).
Угол φ, образованный двумя плоскостями, находится из соотношения:
А1А2+В1В2+С1С2
соs φ = ± ―――――――――――.
√А12+В12+С12 √А22+В22+С22
Условие параллельности двух плоскостей:
А1 В1 С1
― = ― = ―
А2 В2 С2
Условие перпендикулярности плоскостей: А1А2+В1В2+С1С2 = 0.
4. Уравнение прямой в пространстве:
-- как линии пересечения двух плоскостей:
А1х1+В1у+С1z+D1 = 0,
А2х2+В2у+С2z+D2 = 0;
-- проходящей через данную точку М (х1,у1,z1) с направляющим вектором s = (m,n,p):
х – х1 у – у1 z – z1
―― = ―― = ――
m n p
5. Даны две прямые с направляющими векторами s1 = (m1,n1,p1) и s2 = (m2,n2,p2).
Угол φ между двумя прямыми находится из соотношения:
m1m2+n1n2+p1p2
соs φ = ± ―――――――――――
√m12+n12+p12 √m22+n22+p22
Условие параллельности двух прямых в пространстве:
m1 n1 p1
― = ― = ―
m2 n2 p2
Условие перпендикулярности двух прямых в пространстве:
m1m2 + n1n2 + p1p2 = 0.
6. Дана прямая х – х1 у – у1 z – z1
―― = ―― = ―― и плоскость Ах + Ву +Сz + D = 0.
m n p
Угол φ между прямой и плоскостью определяется из соотношения:
│Аm + Bn + Cp│
sin φ = ――――――――――
√А2+В2+С2 √m2+n2+p2
Условие параллельности прямой и плоскости:
Аm + Вn + Cp = 0.
Условие перпендикулярности прямой и плоскости:
А В С
― = ― = ― .
m n р
Семинар№5. Предел функции. Непрерывность функции.
ПЗ № 5. Введение в анализ. Пределы и непрерывность.
1. Разбор домашнего задания №3
2. Найти пределы: 1) 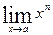 ; 2)
; 2) 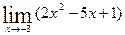
3) 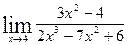 ; 4)
; 4) 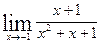 ; 5)
; 5) 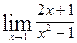
6) 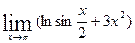 ; 7)
; 7) 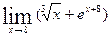
Функция
1. Если каждому элементу (значению) х множества X поставить в соответствие определенный элемент (значение) у множества Y, то говорят, что на множестве X задана функция у = f(х); при этом множество X называется областью определения функции у, а множество Y— областью значений функции y.
2. Функцияy =f(х) называется четной, если для любых значений х из области определения функции f(-х) =f(х), и нечетной, если/(-х) = = -f(x). В противном случаеf(х) — функция общего вида.
3. Функция у =f(х) называется возрастающей (убывающей) на некотором промежутке X, если большему значению аргумента соответствует большее (меньшее) значение функции f(х). Возрастающие или убывающие функции называются монотонными.
4. Функция f(х) называется ограниченной на промежутке X, если существует такое число М > О, что |f(х)| < М, для всех х Є X. В противном случае функция называется неограниченной.
5. Если функция у = f(u) есть функция переменной и (определенной на множестве U с областью значений Y), а переменная и, в свою очередь, также является функцией и = φ(х) (определенной на множестве X с областью значений U), то заданная на множестве X функция у =f[φ(х)] называется сложной функцией.
6. Основные элементарные функции:
а) степенная функция у = хn;
б) показательная функция у = ах, а > 0, а ≠ 1
(Х = (-∞;+∞); Y = (0;+∞));
в) логарифмическая функция у = log ax, а > 0, а ≠ 1
(Х = (0;+∞); Y = (-∞;+∞));
г) тригонометрические функции у=sin х, у = cos х, y= tg х, у = ctg x д) обратные тригонометрические функции у = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
7. Функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
S. Функция у = f(x) называется периодической с периодом Т ≠ 0,
eсли f(x+Т) =f(x) для любых х е X.
9. Преобразования графиков:
a) y=f(x+a)- сдвигает график у =f(x) параллельно оси Ох на a единиц, (а > 0 — влево, а < 0 — вправо);
б) у f(x) + b - сдвигает график у = fix) параллельно оси Оу на b единиц (b>0 — вверх, b < 0 — вниз);
в)у = cf(x) (с ≠ 0) - растягивает в с раз (с > 1) или сжимает (0 < с < 1) графику =f(x) относительно оси Оу; при с < 0 симметрично отображает график относительно оси Ох;
г) у =f(kx) (k≠0) — растягивает в k раз (k > 1) или сжимает (0 <k < 1) график у =f(x) относительно оси Ох; при k < 0 симметрично отображает график относительно оси Оу. 10. Абсолютная величина (модуль) действительного числа х:
x,если х≥0 |x|= х,если х<0.
6. Пределы и непрерывность
1. Если по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число аn то говорят, что задана числовая последовательность (аn).
2. Число А называется пределом числовой последовательности (аn )
если для любого ξ> 0 найдется такой номер N, зависящий от ξ, что для всех членов последовательности с номерами n > N верно неравенство
│an-A│<ξ(lim an=A
3. Число А называется пределом функции y=f(x) при х —> ∞ , если для любого ξ > 0 найдется также число S > О, зависящее от ξ, что для всех х таких, что |х| > S, будет верно неравенство │f(x)-A│<ξ (lim f(x)=A)
4. Функция а(х) называется бесконечно малой величиной при х —> х0 (или х —> ∞ ), если lim а(х) = 0
6. Функция Fх) называется бесконечно большой величиной при х —> х0, если для любого М > 0 найдется такое число δ > 0, зависяoщее от М, что для всех х #хо и удовлетворяющих условию |х - хо| < δ будет верно неравенство
│f(x)│>M(lim F(x)=∞.
Первый замечательный предел.
Lim sin x/x =1
u→0
Второй замечательный предел
Lim (1+1/x)x=e lim (1+y)1/y=e.
x→∞ y→0
Раскрытие неопределенностей различных типов
Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов
Устранить неопределенность удается часто с помощью алгебраических преобразований.
Семинар№6. Производная и дифференциал функции.
ПЗ №6. Дифференциальное исчисление функции одной переменной.
Производная. Дифференциал функции.
1. Разбор домашнего задания №4
2. Пользуясь определением производной, найти производный функций: 1) y=C, где C=const; 2) 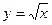 ; 3) y=sinx
; 3) y=sinx
Найти производные функций и вычислить их значения при x=2 и x=0:
1) 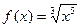 ; 2)
; 2) 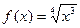 ; 3)
; 3) 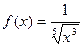
Найти производные следующих функций: 1) y=sin5x; 2) y=cos5x; 3) y=ln(x2+1); 4) y=78x-3; 5) y=(1-2x)50
Определение производной.
1. Производной функции y = f(x) называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):
Δy f (x+Δx) – f (x)
y' = f'(x) = lim ― = lim ―――――― .
Δx→0 Δx Δx→0 Δx
Если функция в точке x0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
2. Если функция y = f ' (x) дифференцируема в точке х0 (или на промежутке Х), то она в этой точке непрерывна (или на промежутке Х). Если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке.
