Тема 1 : Эвристические алгоритмы индивидуального прогнозирования , классификация по одному признаку
План
1.Основная идея классификации по одному признаку с использованием эвристического алгоритма . Обучающий эксперимент .
2.Вероятности принятия ошибочных и верных решений при классификации по одному признаку . ( эвристический алгоритм прогнозирования )
3.Нахождение порогового значения признака при классификации по одному признаку ( эвристический алгоритм прогнозирования )
1.Основная идея классификации по одному признаку с использованием эвристического алгоритма . Обучающий эксперимент .
При оптимальной классификации по одному признаку для решения задачи индивидуального прогнозирования нужно знать двумерную плотность распределения признака и прогнозируемого параметра 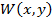 . В оптимальном методе аналитически находится такое пороговое значение признака x – классификации при котором величина средних потерь минимальна . Однако , необходимые при этом аналитические преобразования даже при одном признаке и нормальном совместном законе достаточно сложны . Если же плотность
. В оптимальном методе аналитически находится такое пороговое значение признака x – классификации при котором величина средних потерь минимальна . Однако , необходимые при этом аналитические преобразования даже при одном признаке и нормальном совместном законе достаточно сложны . Если же плотность 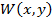 заранее неизвестна то необходим так же статистический эксперимент для нахождения оценки
заранее неизвестна то необходим так же статистический эксперимент для нахождения оценки 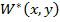 . Решение задачи классификации по одному признаку можно осуществить по данным обучающего эксперимента не прибегая к сложным аналитическим преобразованиям и статистическому эксперименту по определению оценки
. Решение задачи классификации по одному признаку можно осуществить по данным обучающего эксперимента не прибегая к сложным аналитическим преобразованиям и статистическому эксперименту по определению оценки 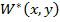 .Если она неизвестна , в этом случае непосредственно по данным обучающего эксперимента подбирается такое пороговое значение признака x – классификации при котором минимальна в соответствии с выбранным критерием требуемая вероятность ошибочных решений . Обычно в качестве такого критерия для подбора x – классификации берется минимум риска потребителя
.Если она неизвестна , в этом случае непосредственно по данным обучающего эксперимента подбирается такое пороговое значение признака x – классификации при котором минимальна в соответствии с выбранным критерием требуемая вероятность ошибочных решений . Обычно в качестве такого критерия для подбора x – классификации берется минимум риска потребителя 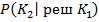 .
.
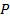 – вероятность
– вероятность
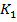 – изделие класса К1 – годное
– изделие класса К1 – годное
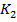 – изделие класса К2 – дефектное
– изделие класса К2 – дефектное
Рассмотрим такой подход на примере прогнозирования стабильности резисторов . Зависимость величины сопротивления резистора от времени представляется в виде линейной модели :
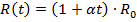
Где 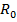 – сопротивление резистора в начальным момент времени
– сопротивление резистора в начальным момент времени 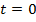 .
. 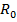 и
и 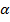 неодинаковы у всех резисторов данного типа , то есть
неодинаковы у всех резисторов данного типа , то есть 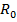 и
и 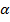 случайные величины с некоторыми плотностями распределения . Отклонение во времени величины сопротивления резистора , то есть нестабильность является следствием неустойчивости его структуры . О степени неустойчивости структуры резистора в значительной мере можно судить по величине фликкерного шума . По – этому в качестве признака характеризующего стабильность резистора можно взять напряжения шума
случайные величины с некоторыми плотностями распределения . Отклонение во времени величины сопротивления резистора , то есть нестабильность является следствием неустойчивости его структуры . О степени неустойчивости структуры резистора в значительной мере можно судить по величине фликкерного шума . По – этому в качестве признака характеризующего стабильность резистора можно взять напряжения шума 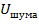 .
.
Прогнозируемым параметром есть величина коэффициента старения 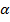 . Пусть для обучающего эксперимента отобрано случайным образом n резисторов . У каждого резистора перед испытанием измерены величины
. Пусть для обучающего эксперимента отобрано случайным образом n резисторов . У каждого резистора перед испытанием измерены величины 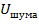 и
и 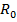 , затем резисторы ставятся на испытания в одинаковом для всех режиме на заданное время прогнозирования , например ,
, затем резисторы ставятся на испытания в одинаковом для всех режиме на заданное время прогнозирования , например , 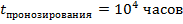
По окончанию испытаний для каждого резистора находится величина коэффициента старения :
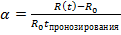
Для того что бы определить номер класса к которому фактически принадлежит каждый из n экземпляров необходимо указать граничное значение прогнозируемого параметра 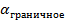 . Оно задается исходя из допустимого отклонения сопротивления резистора за время
. Оно задается исходя из допустимого отклонения сопротивления резистора за время 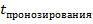 , тогда резисторы с
, тогда резисторы с 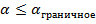 будут отнесены к годным ( классу К1 ) , а резисторы с
будут отнесены к годным ( классу К1 ) , а резисторы с 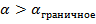 – дефектным ( классу К2 ) .
– дефектным ( классу К2 ) .
Массив исходных для прогнозирования данных полученных в результате обучающего эксперимента будет иметь вид :

S - № класса = 1,2 …
Случайные величины напряжения шума 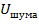 и коэффициент старения
и коэффициент старения 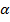 коррелированы и по данным обучающего эксперимента можно построить поле корреляции в виде показанном на рис. 1 .Представленное поле корреляции отображает естественный обусловленный физическими закономерностями характер зависимости коэффициента старения от уровня фликкерного шума .
коррелированы и по данным обучающего эксперимента можно построить поле корреляции в виде показанном на рис. 1 .Представленное поле корреляции отображает естественный обусловленный физическими закономерностями характер зависимости коэффициента старения от уровня фликкерного шума .
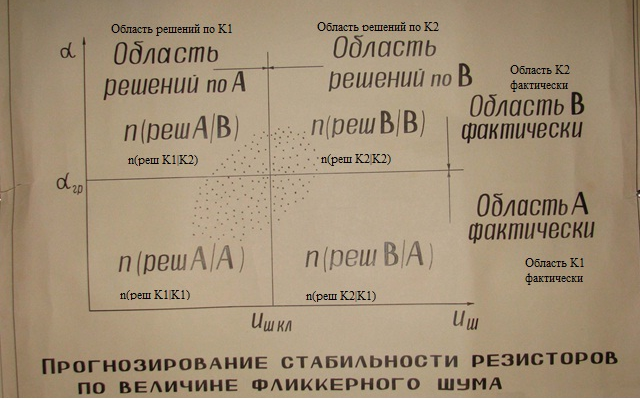
Рисунок 1
Существенная неоднородность структуры резистивного материала приводит к интенсификации процессов старения и значит к увеличению коэффициента старения . На Рис. 1 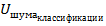 одно из возможных значений величины порога . Измеряя длину для нового резистора
одно из возможных значений величины порога . Измеряя длину для нового резистора 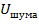 и сравнивая его с
и сравнивая его с 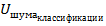 . будем принимать решение об отнесении этого резистора к
. будем принимать решение об отнесении этого резистора к
классу К1 если 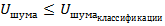
классу К2 если 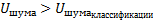
2.Вероятности принятия ошибочных и верных решений при классификации по одному признаку . ( эвристический алгоритм прогнозирования )
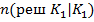 – число верных решений об отнесении экземпляра принадлежащего фактически к классу К1 к этому ж классу , оно равно числу экземпляров у которых по данным обучающего эксперимента
– число верных решений об отнесении экземпляра принадлежащего фактически к классу К1 к этому ж классу , оно равно числу экземпляров у которых по данным обучающего эксперимента 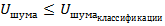 и
и 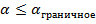 . Это годные экземпляры и по прогнозу они также будут отнесены к годным ( классу К1 ) .
. Это годные экземпляры и по прогнозу они также будут отнесены к годным ( классу К1 ) .
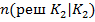 – это число решений у которых
– это число решений у которых 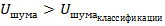 и
и 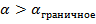 . Это дефектные экземпляры и по прогнозу они будут отнесены к дефектным .
. Это дефектные экземпляры и по прогнозу они будут отнесены к дефектным .
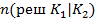 – это число ошибочных решений заключающихся в отнесении экземпляров класса К2 в К1 .Это количество экземпляров
– это число ошибочных решений заключающихся в отнесении экземпляров класса К2 в К1 .Это количество экземпляров 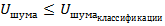 и
и 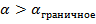
Это фактически дефектные экземпляры класс К2 которые по прогнозу будут отнесены к годным ( класс К1 )
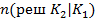 – число ошибочных решений … при
– число ошибочных решений … при 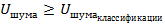 и
и 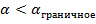 .
.
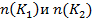 – число экземпляров фактически принадлежащих к классу К1 и К2 соответственно , при этом их сумма равна числу экземпляров используемых в обучающем эксперименте
– число экземпляров фактически принадлежащих к классу К1 и К2 соответственно , при этом их сумма равна числу экземпляров используемых в обучающем эксперименте 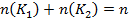 .
.
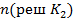 и
и 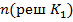 – общее число решений принимаемых об отнесении экземпляров соответственно к классу К1 или К2 по прогнозу при этом
– общее число решений принимаемых об отнесении экземпляров соответственно к классу К1 или К2 по прогнозу при этом 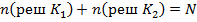 .
.
Для введенных характеристик справедливы соотношения :
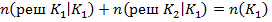
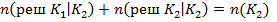
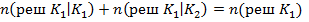
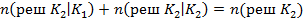
Справедливость приведенных выше соотношений следует из Рис. 1 .Теперь можно определить оценки вероятности ошибочных и верных решений и априорных вероятностей .
Риск потребителя
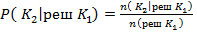 ( 1 )
( 1 )
Риск изготовителя
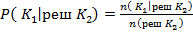 ( 2 )
( 2 )
Условные вероятности принятия ошибочных решений
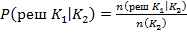 ( 3 )
( 3 )
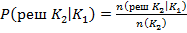 ( 4 )
( 4 )
Априорные вероятности принадлежности экземпляра к классу К1 ( вероятность оказаться годным любого взятого наугад экземпляра ):
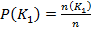 ( 5 )
( 5 )
и к классу К2 (вероятность оказаться дефектным любого взятого наугад экземпляра ) :
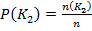 ( 6 )
( 6 )
Априорные вероятности принятия решения об отнесении экземпляра к классу К1 :
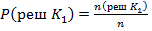 ( 7 )
( 7 )
и к классу К2 :
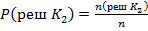 ( 8 )
( 8 )
Если качество прогнозирования необходимо оценить каким – либо одним показателем учитывающим одновременно ошибки того и другого вида можно использовать вероятность ошибки : 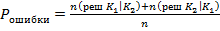 ( 9 )
( 9 )
вероятность принятия правильных решений ( эффективность распознавания )
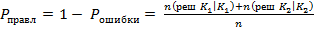 ( 10 )
( 10 )
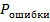 и
и 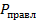 нужно использовать для оценки качества прогнозирования когда потери от переименования К1 в К2 и К2 в К1 одинаковы .
нужно использовать для оценки качества прогнозирования когда потери от переименования К1 в К2 и К2 в К1 одинаковы .
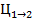 и
и 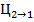 – цена переименования
– цена переименования
3.Нахождение порогового значения признака при классификации по одному признаку ( эвристический алгоритм прогнозирования )
Значение 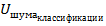 должно быть выбрано таким образом чтобы вероятности ошибочных решений не превышали допустимого уровня .
должно быть выбрано таким образом чтобы вероятности ошибочных решений не превышали допустимого уровня .
Если 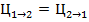 то наилучшим значением
то наилучшим значением 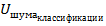 будет такое при котором общее количество ошибочных решений того и другого вида минимальна . Однако на практике чаще всего стремятся к минимальному или допустимому риску потребителя ( 1 ) так как цены переименования как правило неодинаковы , обычно
будет такое при котором общее количество ошибочных решений того и другого вида минимальна . Однако на практике чаще всего стремятся к минимальному или допустимому риску потребителя ( 1 ) так как цены переименования как правило неодинаковы , обычно 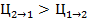 – тогда наилучшим значением
– тогда наилучшим значением 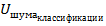 будет такое при котором достигается это значение риска потребителя . Величина порога может быть определенна путем расчета нескольких вариантов и выбором такого
будет такое при котором достигается это значение риска потребителя . Величина порога может быть определенна путем расчета нескольких вариантов и выбором такого 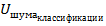 при котором требования заданные относительно величин
при котором требования заданные относительно величин 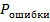 или
или 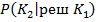 выполняются . Если этим требованиям не удается удовлетворить не при каком значении
выполняются . Если этим требованиям не удается удовлетворить не при каком значении 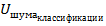 следует попытаться использовать большее число признаков либо найти более информативные признаки . Представляет интерес рассмотреть на примере как изменяются риски
следует попытаться использовать большее число признаков либо найти более информативные признаки . Представляет интерес рассмотреть на примере как изменяются риски 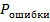 и другие вероятности в зависимости от величины порога
и другие вероятности в зависимости от величины порога 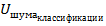 . Пусть для обучающего эксперимента случайным образом отобрано 20 резисторов (
. Пусть для обучающего эксперимента случайным образом отобрано 20 резисторов ( 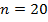 ) В реальных задачах рекомендуется брать
) В реальных задачах рекомендуется брать 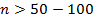 .Приемлемая величина объема выборки
.Приемлемая величина объема выборки 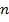 определяется степенью разброса признаков и прогнозированного параметра и требованиями к точности оценки ошибки прогнозирования . Результат обучающего эксперимента отображены на поле корреляции признака
определяется степенью разброса признаков и прогнозированного параметра и требованиями к точности оценки ошибки прогнозирования . Результат обучающего эксперимента отображены на поле корреляции признака 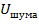 и прогнозируемого параметра ( см . Рис 2 )
и прогнозируемого параметра ( см . Рис 2 )

Рисунок 2А
Значения 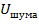 и
и 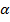 какого – либо резистора задают координаты соответствующей точки на поле корреляции , для простоты по оси абсцисс отложены условные единицы 0 – 12 , по оси ординат указано некоторое граничное значения коэффициента старения
какого – либо резистора задают координаты соответствующей точки на поле корреляции , для простоты по оси абсцисс отложены условные единицы 0 – 12 , по оси ординат указано некоторое граничное значения коэффициента старения 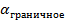 которое устанавливается исходя из конкретных условий применения резистора . Как следует из расположения точек на поле корреляции относительно
которое устанавливается исходя из конкретных условий применения резистора . Как следует из расположения точек на поле корреляции относительно 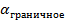 оценки априорных вероятностей принадлежность резистора к классу К1 и К2 , ( 5 ) и ( 6 ) равны соответственно:
оценки априорных вероятностей принадлежность резистора к классу К1 и К2 , ( 5 ) и ( 6 ) равны соответственно:
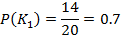
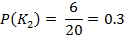
Изменяя величину порога 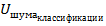 мы будем изменять общее число решений об отнесении резистора к тому или иному классу
мы будем изменять общее число решений об отнесении резистора к тому или иному классу 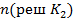 ,
, 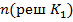 и вместе с тем число ошибочных решений
и вместе с тем число ошибочных решений 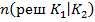 и
и 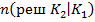 и число верных решений
и число верных решений 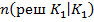 и
и 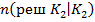 соответственно будут изменяться и все рассмотренные ранее вероятности . На рисунке 2Б представлены сглаженные кривые зависимости этих вероятностей от величины порога и расчетные точки по данным из таблицы 1.
соответственно будут изменяться и все рассмотренные ранее вероятности . На рисунке 2Б представлены сглаженные кривые зависимости этих вероятностей от величины порога и расчетные точки по данным из таблицы 1.
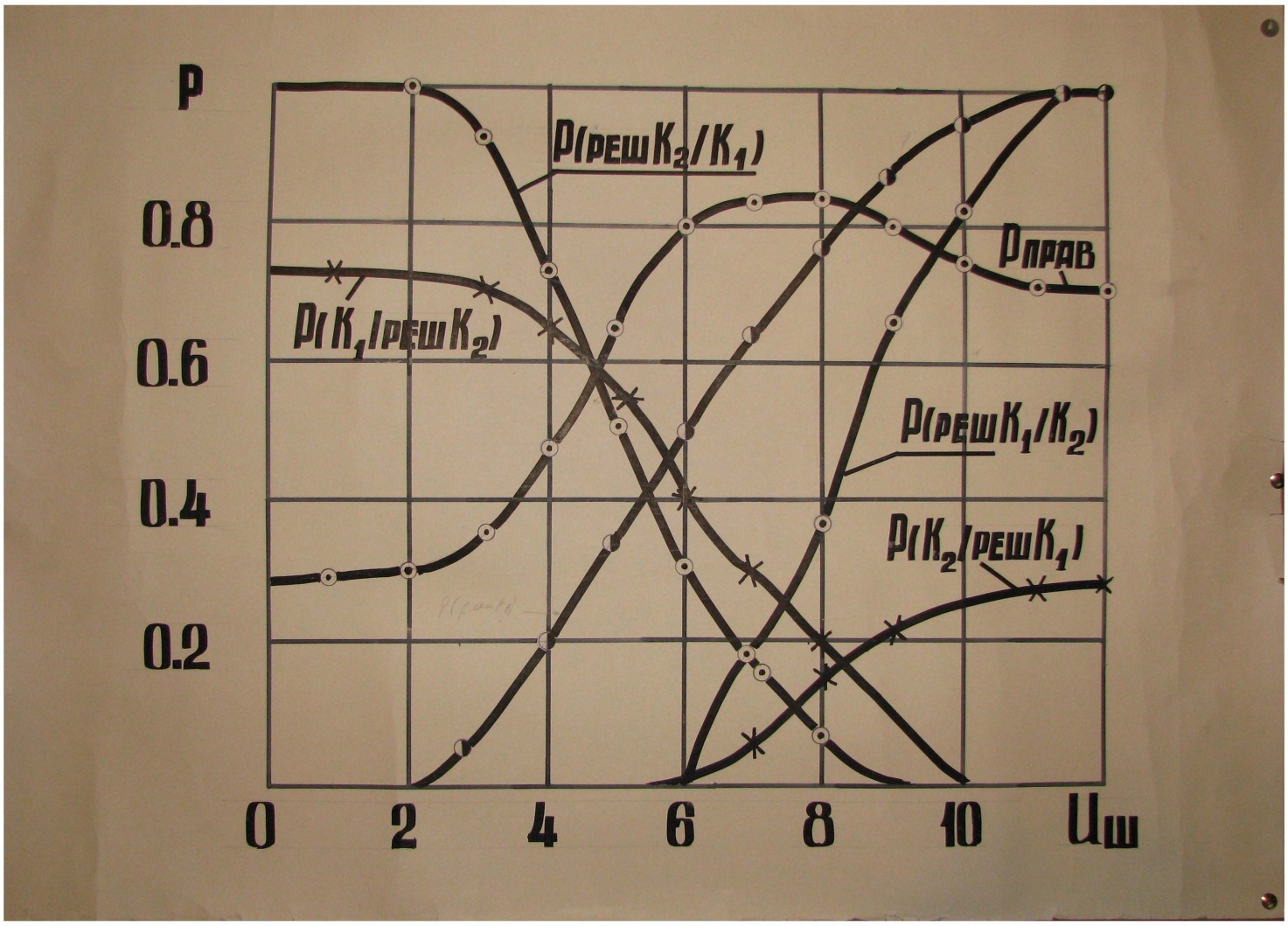
Рисунок 2Б
Расхождение между кривыми и расчетными точками в этом примере обусловлено ограниченностью объема выборки . Рассмотрение этих зависимостей приводит к выводам :
риск изготовителя с увеличением порога уменьшается от 0.7 до 0 . Его максимальное значение равно априорной вероятности 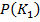 . То есть
. То есть 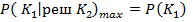 . Риск потребителя с увеличением порога возрастает от 0 до 0.3 . Его максимальное значение равно априорной вероятности
. Риск потребителя с увеличением порога возрастает от 0 до 0.3 . Его максимальное значение равно априорной вероятности 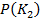 , те есть
, те есть 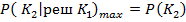 . Чем меньше
. Чем меньше 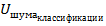 тем больше риск изготовителя и меньше риск потребителя , но и тем дороже резисторы так как при этом большее их число будет , по результатам прогнозирования , отнесено к классу К2 то есть к дефектным .
тем больше риск изготовителя и меньше риск потребителя , но и тем дороже резисторы так как при этом большее их число будет , по результатам прогнозирования , отнесено к классу К2 то есть к дефектным .
Вероятность принятия правильных решений 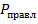 с увеличением порога возрастает от значения априорной вероятности
с увеличением порога возрастает от значения априорной вероятности 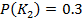 до некоторого значения определяемого наибольшим количеством верных решений в нашем случае до 0.85 , а затем снижается до величины априорной вероятности
до некоторого значения определяемого наибольшим количеством верных решений в нашем случае до 0.85 , а затем снижается до величины априорной вероятности 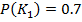 Вероятность ошибочных решений
Вероятность ошибочных решений 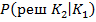 с ростом порога уменьшается от 1 до 0 так как при этом уменьшается до 0 число ошибочных решений
с ростом порога уменьшается от 1 до 0 так как при этом уменьшается до 0 число ошибочных решений 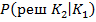 . Аналогичная вероятность
. Аналогичная вероятность 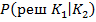 увеличивается от 0 до 1 так как при этом число ошибочных решений возрастает от 0 то своего максимального значения в нашем случае до 6 . Вероятность отнесения к годным по прогнозу
увеличивается от 0 до 1 так как при этом число ошибочных решений возрастает от 0 то своего максимального значения в нашем случае до 6 . Вероятность отнесения к годным по прогнозу 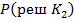 с увеличением
с увеличением 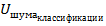 возрастает от 0 до 1 так как при этом число решений об отнесении экземпляра к классу К1 возрастает от 0 до своего максимального значения , в нашем случае до 20 . Своих предельных значений рассматриваемой вероятности достигают как правило при таком минимальном и максимальном значениях порога
возрастает от 0 до 1 так как при этом число решений об отнесении экземпляра к классу К1 возрастает от 0 до своего максимального значения , в нашем случае до 20 . Своих предельных значений рассматриваемой вероятности достигают как правило при таком минимальном и максимальном значениях порога 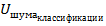 которое находится вне интервала значений
которое находится вне интервала значений 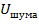 полученных по данным обучающего эксперимента (см. Рис. 2 )
полученных по данным обучающего эксперимента (см. Рис. 2 )
Кривые вероятности 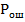 и
и 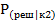 на рисунке на 2А не преведены так как эти вероятности равны соответственно :
на рисунке на 2А не преведены так как эти вероятности равны соответственно :
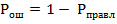 ;
; 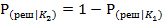
Таким образом меняя 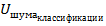 можно влиять на результат прогнозирования , но при этом нужно учитывать , что все вероятности взаимосвязанные . Если необходимо уменьшить риск потребителя не повышая при этом число резисторов ошибочно отнесенных по прогнозу к дефектным следует совершенствовать процедуру прогнозирования причём наиболее перспективным направлением является отыскание новых и возможно более информативных признаков , либо повысить качество изготовляемых резисторов совершенствуя технологию и качество материалов.
можно влиять на результат прогнозирования , но при этом нужно учитывать , что все вероятности взаимосвязанные . Если необходимо уменьшить риск потребителя не повышая при этом число резисторов ошибочно отнесенных по прогнозу к дефектным следует совершенствовать процедуру прогнозирования причём наиболее перспективным направлением является отыскание новых и возможно более информативных признаков , либо повысить качество изготовляемых резисторов совершенствуя технологию и качество материалов.
Следует иметь в виду что уменьшение риска потребителя должно сочетаться с экономически приемлемым риском изготовителя и вероятностью отнесения к годному прогнозу 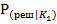 .
.
Тема 2 : Индивидуальное прогнозирование по признакам с оценкой значения прогнозируемого параметра с использованием теории статистических оценок.
ПЛАН
1.Оптимальная оценка значения прогнозируемого параметра с использованием теории статистических оценок.
2. Условия необходимые для реализации индивидуального прогнозирования по признакам с использованием теории статистических оценок.
3. Оптимальное оценивание прогнозируемого параметра по одному признаку
1 ) Расмотрим решение задачи индивидуального прогнозирования по признаку с оценкой значения прогнозируемого параметра методами теории статистических оценок, полагая, что многомерная совместная плотность распределения значений признака и прогнозируемого параметра известна , то есть известно ее аналитическое выражение .Пусть начальное состояние изделия оценивается k – признакими каждый из которых случайная величина . Обозначим эту совокупность k -случайных величин :
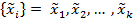 .
.
По конкретным значениям признаков : 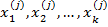
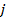 - того экземпляра необходимо найти оценку значения прогнозируемого параметра
- того экземпляра необходимо найти оценку значения прогнозируемого параметра 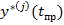 ,
, 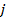 – номер экземпляра , * - оценка , к моменту времени
– номер экземпляра , * - оценка , к моменту времени 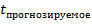 , который для простоты будем обозначать
, который для простоты будем обозначать 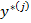 Задачу прогнозирования значения параметра по признакам имеет смысл ставить только в том случае когда каждый из признаков
Задачу прогнозирования значения параметра по признакам имеет смысл ставить только в том случае когда каждый из признаков 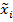 и прогнозируемый параметр
и прогнозируемый параметр 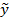 являются зависимыми случайными величинами . Степень их зависимости определяется видом многомерной совместной плотности распределения значений признаков
являются зависимыми случайными величинами . Степень их зависимости определяется видом многомерной совместной плотности распределения значений признаков 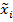 и прогнозируемом параметром
и прогнозируемом параметром 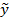 :
:
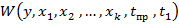
Который для простоты будем обозначать далее как :
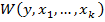 (1)
(1)
Если прогнозируемый параметр с каждым из признаков независим, то прогнозирование теряет смысл и эта многомерная плотность распределения вырождается в произведении 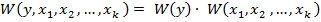 (2)
(2)
одномерной плотности значений прогнозируемого параметра 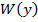 и совместной плотности распределения признаков.
и совместной плотности распределения признаков.
Прогнозирование должно быть точным. В качестве количестве количественной меры точности естественновзять дисперсию ошибки 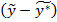 в оценке прогнозируемого параметра.
в оценке прогнозируемого параметра.
Где
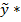 - оценка параметра
- оценка параметра 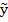
Тогда критерий оптимальности имеет вид :
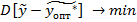 (3)
(3)
где
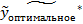 - оптимальная оценка параметра
- оптимальная оценка параметра 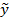 .
.
Интегрируя выражение (1) по переменной y в пределах -∞ до +∞ получим:
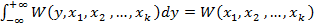 (4)
(4)
k – мерную плотность совместного распределения признаков.
Тогда условная плотность распределения прогнозируемого параметра 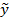 при условии, что признаки случайные величины
при условии, что признаки случайные величины 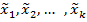 примет некоторое значения
примет некоторое значения 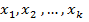 равна:
равна:
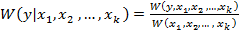 (5)
(5)
Если у какого – либо 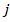 – го экземпляра измерить значение признаков
– го экземпляра измерить значение признаков 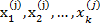 и подставить это в выражение (5) получим условную плотность распределения прогнозируемого параметра для этого
и подставить это в выражение (5) получим условную плотность распределения прогнозируемого параметра для этого 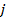 – го экземпляра, при условии что признаки
– го экземпляра, при условии что признаки 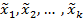 приняли именно эти значения, соответственно
приняли именно эти значения, соответственно 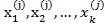 получаем такую условную плотность:
получаем такую условную плотность:
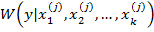 (6) ;
(6) ;
Эта плотность есть функция одной переменной (у). Отметим, что дисперсия, вычисленная по плотности (6), будет меньше дисперсии, вычисляемой по плотности 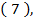 и различие между ними будет тем существеннее, чем сильнее зависимость между каждой из случайных величин
и различие между ними будет тем существеннее, чем сильнее зависимость между каждой из случайных величин 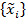 и прогнозируемым параметром, а так же чем менее при этом
и прогнозируемым параметром, а так же чем менее при этом 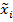 зависимы между собой.
зависимы между собой.
В качестве оценки 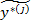 прогнозируемого параметра
прогнозируемого параметра 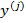 берется наиболее вероятное значение случайной величины
берется наиболее вероятное значение случайной величины 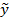 - её мода, то есть такое, при котором плотность распределения (6) максимальна. Предположим, что эта плотность имеет одну единственную моду. Такая оценка имеет наименьшую дисперсию ошибки по сравнению со всеми другими возможными оценками ( медиана, математическое ожидание). Эта оценка следовательно удовлетворяет критерий оптимальности (3) то есть является оптимальной оценкой прогнозируемого параметра
- её мода, то есть такое, при котором плотность распределения (6) максимальна. Предположим, что эта плотность имеет одну единственную моду. Такая оценка имеет наименьшую дисперсию ошибки по сравнению со всеми другими возможными оценками ( медиана, математическое ожидание). Эта оценка следовательно удовлетворяет критерий оптимальности (3) то есть является оптимальной оценкой прогнозируемого параметра 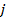 – го экземпляра, обозначим её
– го экземпляра, обозначим её 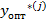 .Таким образом прогнозирование оптимально, когда оценка
.Таким образом прогнозирование оптимально, когда оценка 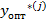 находится из выражения :
находится из выражения :
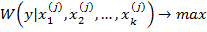 (7)
(7)
Оценка 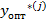 полученная из выражения ( 7 ) будет иметь в действительности некоторое рассеивание относительно фактического значения
полученная из выражения ( 7 ) будет иметь в действительности некоторое рассеивание относительно фактического значения 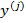 прогнозируемого параметра
прогнозируемого параметра 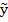 , но это рассеивание будет наименьшим из возможных и следовательно ошибки в прогнозировании при использовании этого метода будут средне минимальными . На рис 1 иллюстрируется эффективность прогнозирования с помощью условной плотности ( 6 ) по сравнению с оценкой параметров
, но это рассеивание будет наименьшим из возможных и следовательно ошибки в прогнозировании при использовании этого метода будут средне минимальными . На рис 1 иллюстрируется эффективность прогнозирования с помощью условной плотности ( 6 ) по сравнению с оценкой параметров 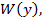 которое представляет безусловную плотность распределения прогнозируемого параметра к моменту времени
которое представляет безусловную плотность распределения прогнозируемого параметра к моменту времени 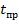 .
.
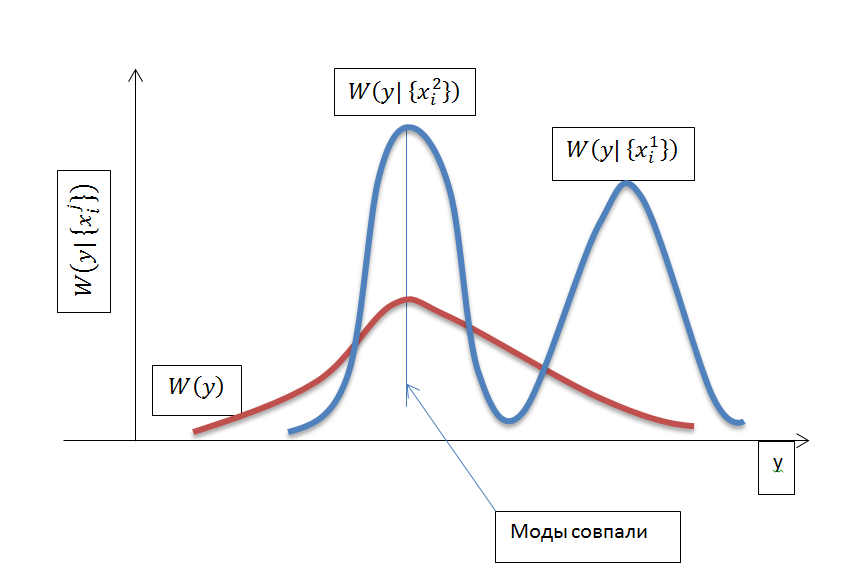
Рисунок 1
Как следует из рис 1 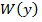 независящая от конкретных значений признаков имеет большую дисперсию, чем
независящая от конкретных значений признаков имеет большую дисперсию, чем 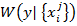 , а значит и ошибка полученная при использовании оценки параметра по безусловной плотности
, а значит и ошибка полученная при использовании оценки параметра по безусловной плотности 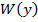 имеет большую дисперсию.
имеет большую дисперсию.
Индивидуальное прогнозирование по признакам будет тем эффективней, если существенно уменьшить дисперсию ошибки индивидуального прогнозирования по сравнению с дисперсией безусловной плотности 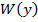 ,а это в первую очередь определяется степенью зависимости между прогнозируемым параметром и признаками ( Рис 1 ) . Расположения условной плотности ( 6 ) относительной безусловной плотности
,а это в первую очередь определяется степенью зависимости между прогнозируемым параметром и признаками ( Рис 1 ) . Расположения условной плотности ( 6 ) относительной безусловной плотности 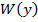 зависит от конкретного набора значений признаков
зависит от конкретного набора значений признаков 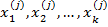 ,
, 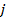 -го экземпляра и степени коррелированности признаков с прогнозируемым параметром (см . Рис 1) и в общем случае может иметь вид кривой
-го экземпляра и степени коррелированности признаков с прогнозируемым параметром (см . Рис 1) и в общем случае может иметь вид кривой 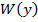 при условии
при условии 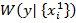 ) , где i – номер признака, j – экземпляра. Если же измеренные значения оказались равными соответствующим модальным значениям
) , где i – номер признака, j – экземпляра. Если же измеренные значения оказались равными соответствующим модальным значениям 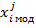 случайных величин
случайных величин 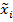 то условная плотность будет располагаться как кривая
то условная плотность будет располагаться как кривая 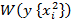 (см . Рис 2 )
(см . Рис 2 )
Дисперсия условной плотности будет тем меньше чем более коррелированы признаки с параметром . Таким образом рассмотренный теоретически строгий подход дает оптимальную оценку прогнозируемому параметру .
2. Условия необходимые для реализации индивидуального прогнозирования по признакам с использованием теории статистических оценок .
Практическое применение рассмотренного метода возможны если проведен специальный эксперимент по сбору и обработке статистических данных о прогнозируемом параметре и признаках в результате которой найдены подходящие аналитические модели условных многомерных плотностей распределения прогнозируемого параметра и признаков , однако на практике специалист сталкивается здесь с массой проблем , по - этому реализовать этот метод можно далеко не всегда . Во первых : для реальных комплектующих элементов устройств и изделий даже при известной совокупности информативных признаков ( выявление которых так же представляет весьма трудоемкую задачу ) Не всегда известны многомерные условные плотности распределения признаков и прогнозируемого параметра . Во-вторых : получение аналитических моделей этих условных плотностей распределения признаков представляет трудоемкий процесс и может быть поставлена только отдельной самостоятельной задачей для каждого типа изделий и его условий эксплуатации . В – третьих : даже если такие аналитические модели получены , необходимые в этом методе прогнозирования аналитические преобразования достаточно сложны. Задача относительно легко решается , если многомерные условные плотности подчиняются нормальному закону .
3. Оптимальное оценивание прогнозируемого параметра по одному признаку
Рассмотрим пример оптимального оценивания прогнозируемого параметра , когда начальное состояние изделия оценивается всего одним признаком и совместная плотность распределения этого признака и прогнозируемого параметра подчиняется нормальному закону. Вариант оптимального оценивания рассмотрим применив к задаче прогнозирования долговечности мощных транзисторов по величине теплового соединения между кристаллом и корпусом .
Известно , что увеличение теплового сопротивления основной причиной которого есть некачественная пайка или приклейка кристаллов к корпусу что приводит к повышенному нагреву кристалла и снижению срока службы транзисторов . В качестве признака характеризующего величину теплового сопротивления и следовательно долговечность транзистора принять температуру перегрева транзистора под определенной нагрузкой в течении заданного времени ( обычно в течении нескольких секунд ) А в качестве прогнозируемого параметра выбирается долговечность транзистора .
Коэффициент корреляции между долговечностью и температурой перегрева отрицательный , так как чем больше казалось 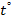 перегрева , тем более вероятна что его долговечность будет ниже .
перегрева , тем более вероятна что его долговечность будет ниже .
Сохраняя принятые ранее обозначения считаем признаком случайную величину 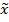 температуру перегрева транзистора . а прогнозируемым параметром случайную величину
температуру перегрева транзистора . а прогнозируемым параметром случайную величину 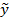 – долговечность транзистора .
– долговечность транзистора .
Оценка начального состояния каждого экземпляра заключается здесь в измерении температуры перегрева транзистора . Задача индивидуального прогнозирования состоит в оценке по температуре перегрева каждого экземпляра его долговечности .
Как показывает опыт совместная плотность распределения значения признака и прогнозируемого параметра может быть описана двумерным нормальным законом распределения случайных величин 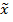 и
и 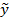 .
.
Выражение этой плотности имеет вид :
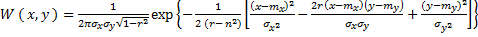 (8)
(8)
где :
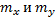 – математическое ожидание признака и прогнозируемого параметра соответственно .
– математическое ожидание признака и прогнозируемого параметра соответственно .
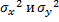 – дисперсии признака и прогнозируемого параметра соответственно .
– дисперсии признака и прогнозируемого параметра соответственно .
r – коэффициент корреляции между признаком и прогнозируемым параметром .
Одномерные плотности распределения признака и прогнозируемого параметра определяется выражениями :
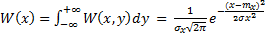 ( 9 )
( 9 )
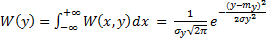 ( 10 )
( 10 )
Разделив выражение 8 на 9 получим :
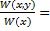 условную плотность распределения прогнозируемого параметра
условную плотность распределения прогнозируемого параметра 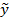 , при условии , что признак
, при условии , что признак 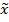 принял некоторое значение x .
принял некоторое значение x .
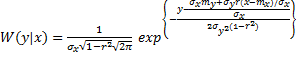 ( 11 )
( 11 )
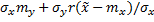 ---- условная мат. ожидания
---- условная мат. ожидания 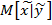
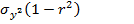 ----------
---------- 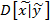 условная дисперсия
условная дисперсия
Из выражения ( 11 ) следует , что полученная условная плотность распередения случайной величины 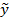 – есть нормальный закон с математическим ожиданием
– есть нормальный закон с математическим ожиданием 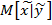 и дисперсией
и дисперсией 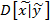 равным соответственно :
равным соответственно :
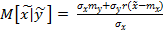 ( 12 )
( 12 )
если 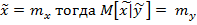 ( см. рис. 1)
( см. рис. 1)
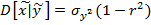 ( 13 )
( 13 )
Если 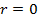 – нет корреляции между признаками и параметрами , то :
– нет корреляции между признаками и параметрами , то :
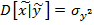 Как следует из выражения 12 , 13 условное математическое ожидание прогнозируемого параметра зависит от того какое значения приняла случайная величина
Как следует из выражения 12 , 13 условное математическое ожидание прогнозируемого параметра зависит от того какое значения приняла случайная величина 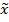 – то есть признак ,а условная дисперсия
– то есть признак ,а условная дисперсия 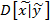 не зависит от значений признака и определяется степенью значения корреляции между
не зависит от значений признака и определяется степенью значения корреляции между 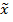 и
и 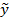
Если в выражении ( 12 ) подставить измеренное значения признака 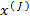 ( t
( t  перегрева
перегрева 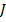 – го экземпляра ) получим условную плотность распределения долговечности этого
– го экземпляра ) получим условную плотность распределения долговечности этого 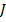 – го транзистора , при условии , что его t
– го транзистора , при условии , что его t  перегрева , оказалась равной именно этому значению
перегрева , оказалась равной именно этому значению 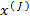 . Эта плотность распределения имеет вид :
. Эта плотность распределения имеет вид :
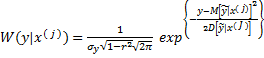 ( 14 )
( 14 )
Эта плотность – функция одной переменной – y . Оптимальной оценкой прогнозируемого параметра – долговечности является мода плотности распределения ( 14) то есть такое значение при котором эта плотность максимальна . Так как выражение ( 14 ) представляет нормальное распределение у которого мода совпадает с математическим ожиданием оптимальная оценка долговечности какого – либо конкретного 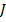 – го транзистора равна :
– го транзистора равна :
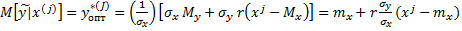 ( 15 )
( 15 )
Измерив величину температуры перегрева 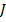 – го транзистора и подставив в это значение выражение ( 15 ) определим оптимальную оценку долговечности этого транзистора
– го транзистора и подставив в это значение выражение ( 15 ) определим оптимальную оценку долговечности этого транзистора 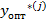 , однако ,
, однако , 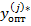 есть только оценка и поскольку признак b прогнозированный параметр связаны вероятностью действительное значение прогнозируемого параметра
есть только оценка и поскольку признак b прогнозированный параметр связаны вероятностью действительное значение прогнозируемого параметра 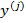 в момент
в момент  будет отличаться от
будет отличаться от 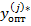 , где определение точности прогнозирования необходимо выявить степень рассеивания оценки
, где определение точности прогнозирования необходимо выявить степень рассеивания оценки 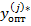 относительно фактических
относительно фактических 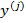 .
.
Можно показать , что отклонение 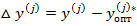 имеет математическое ожидание
имеет математическое ожидание
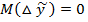 ( 16 )
( 16 )
и дисперсию 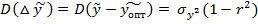 ( 17 )
( 17 )
На рисунке 2 показана зависимость дисперсии ошибки от величины коэффициента корреляции r между случайными величинами 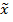 и
и 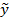 из которой следует , что чем сильнее коррелируемый признак и прогнозируемый параметр тем меньше дисперсия ошибки прогнозирования . С увеличением дисперсии прогнозируемого параметра
из которой следует , что чем сильнее коррелируемый признак и прогнозируемый параметр тем меньше дисперсия ошибки прогнозирования . С увеличением дисперсии прогнозируемого параметра 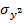 при том же коэффициенте корреляции r дисперсия ошибки возрастает .
при том же коэффициенте корреляции r дисперсия ошибки возрастает .
Рисунок 2 Рисунок 3
Если случайные величины 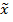 и
и 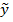 не коррелированы r = 0 то дисперсия ошибки прогнозирования равна дисперсии прогнозируемого параметра. Если же между случайными величинами
не коррелированы r = 0 то дисперсия ошибки прогнозирования равна дисперсии прогнозируемого параметра. Если же между случайными величинами 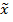 и
и 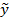 жесткая функциональная связь те есть
жесткая функциональная связь те есть 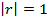 , то дисперсия ошибки прогнозирования равна нулю при любой дисперсии прогнозированного параметра
, то дисперсия ошибки прогнозирования равна нулю при любой дисперсии прогнозированного параметра 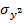 .
.
Если прогнозируемый параметр является линейной функцией признака . то независимо от рассеивания прогнозируемого параметра его значение определяется значением признака 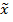 и видом этой линейной функции.
и видом этой линейной функции.
На рис 3 показано как меняется расположения условной плотности 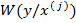 относительно одномерной плотности
относительно одномерной плотности 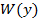 в зависимости от коэффициента корреляции r и конкретного значения признака
в зависимости от коэффициента корреляции r и конкретного значения признака 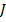 – го экземпляра
– го экземпляра 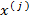 . При оценивании прогнозированного параметра по
. При оценивании прогнозированного параметра по 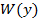 в качестве оценки естественно брать моду этого распределения
в качестве оценки естественно брать моду этого распределения 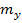 . При оптимальном прогнозировании оценка берется равно моде условного распределения
. При оптимальном прогнозировании оценка берется равно моде условного распределения 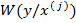 полученного из условия , что признак
полученного из условия , что признак 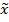 принял некоторое конкретное значение
принял некоторое конкретное значение 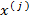 . Для рассматриваемого примера индивидуального прогнозирования долговечности мощных транзисторов , по величине температуры перегрева рассчитаны кривые плотности условного распределения
. Для рассматриваемого примера индивидуального прогнозирования долговечности мощных транзисторов , по величине температуры перегрева рассчитаны кривые плотности условного распределения 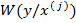 для двух значений коэффициента корреляции между долговечностью и температурой перегрева и четырех значений признака (
для двух значений коэффициента корреляции между долговечностью и температурой перегрева и четырех значений признака ( 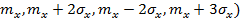 , а так же рассчитаны кривые безусловной плотности распределения
, а так же рассчитаны кривые безусловной плотности распределения 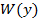 на рисунке 3 обозначены :
на рисунке 3 обозначены :
кривая 1 – безусловная плотность распределения прогнозируемого параметра 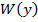
кривая 2 – условная плотность 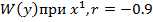 .
.
кривая 3 – условная плотность при 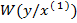 при
при 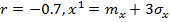
кривая 4 – условная плотность при 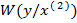 при
при 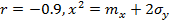
кривая 5 - *||*||*||* 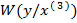 при
при 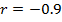
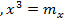
В данном случае признак равен моде и математическому ожиданию
кривая 6 - *||*||*||* 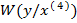 при
при 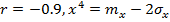 .
.
Сравнивая кривую 1 со всеми остальными , видим что последние характерны меньшим рассеиванием и оно тем меньше чем больше коэффициент корреляции между признаками и прогнозируемым параметром . Так как кривые 2,4,5 соответствуют 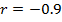
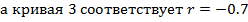 . Чем более зависимы признаки прогнозируемого параметра , тем меньше дисперсия условного распределения параметра и следовательно меньше ошибки прогнозирования . Положение моды условного распределения зависит от r и от конкретного значения
. Чем более зависимы признаки прогнозируемого параметра , тем меньше дисперсия условного распределения параметра и следовательно меньше ошибки прогнозирования . Положение моды условного распределения зависит от r и от конкретного значения 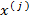 признака
признака 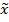 . Это следует из выражения 16 и отображено на рис 3 . Исключением является случай когда признак
. Это следует из выражения 16 и отображено на рис 3 . Исключением является случай когда признак 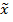 принял значение
принял значение 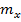 (кривая 5 ) при этом не зависимо от величины коэффициента корреляции мода условной плотности
(кривая 5 ) при этом не зависимо от величины коэффициента корреляции мода условной плотности 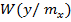 равна
равна 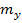 . Сравнение кривых 3 и 4 показывает , что при одном и том же значение признака
. Сравнение кривых 3 и 4 показывает , что при одном и том же значение признака 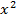 , чем больше модуль коэффициента корреляции , тем сильнее проявляется влияние этого
, чем больше модуль коэффициента корреляции , тем сильнее проявляется влияние этого 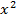 на значение
на значение 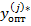 (назначение моды условного распределения ) Сравнивая кривые 2 и 4 видим что чем больше
(назначение моды условного распределения ) Сравнивая кривые 2 и 4 видим что чем больше 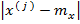 тем (при том же модуле r ) дальше от
тем (при том же модуле r ) дальше от 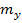 находится мода условного распределения
находится мода условного распределения 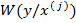 , то есть тем значительней оценка
, то есть тем значительней оценка 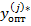 отличается от
отличается от 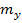 . Изменение знака коэффициента корреляции не меняет форму кривой , а лишь изменяет ее положение относительно
. Изменение знака коэффициента корреляции не меняет форму кривой , а лишь изменяет ее положение относительно 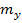 , в зависимости от значений признаков
, в зависимости от значений признаков 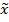 .
.
по – этому кривая 4 есть так же условная плотность 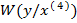 при
при 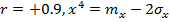 а симметричная ей относительно
а симметричная ей относительно 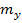 кривая 6 имеет такой вид так же при
кривая 6 имеет такой вид так же при 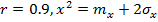 . Рассмотрение кривых рисунков 3 убеждает в том , что индивидуальное прогнозирование по признакам с использованием условной плотности
. Рассмотрение кривых рисунков 3 убеждает в том , что индивидуальное прогнозирование по признакам с использованием условной плотности 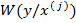 существенно сужает дисперсию ошибки по сравнению с оцениванием параметра по
существенно сужает дисперсию ошибки по сравнению с оцениванием параметра по 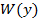 и тем более чем сильнее коррелируемы признаки с прогнозируемым параметром . Рассмотренный пример оптимального прогнозирования для случая когда признаки прогнозирующие параметр имеют совместное нормальное распределения позволяют детально исследовать свойства оптимальной оценки прогнозированного параметра
и тем более чем сильнее коррелируемы признаки с прогнозируемым параметром . Рассмотренный пример оптимального прогнозирования для случая когда признаки прогнозирующие параметр имеют совместное нормальное распределения позволяют детально исследовать свойства оптимальной оценки прогнозированного параметра 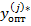 , а так же влияние на нее различных параметров распределения таких как
, а так же влияние на нее различных параметров распределения таких как 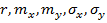 и конкретного значения признака
и конкретного значения признака 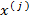 . Для других практически встречающихся законов совместного распределения признаков прогнозирования параметра качественный характер приведенных примеров сохраняется . Их исследование связано с определенными математическими трудностями .
. Для других практически встречающихся законов совместного распределения признаков прогнозирования параметра качественный характер приведенных примеров сохраняется . Их исследование связано с определенными математическими трудностями .
Тема 3 : Алгоритм оптимальной классификации
План
1.Теория статистической классификации.
2.Вероятности принятия ошибочных решений при оптимальной классификации .
3.Критерий Байеса. Отношение правдоподобия
4.Вероятностиные характеристики при оптимальной классификации по оптимальному признаку.
5.Нахождение порогового значения признака при оптимальной классификации .
6.Влияние параметров совместного распределения на вероятность принятия ошибочных решений при оптимальной классификации.
7.Взаимное расположение безусловных и условных плотностей распределения для индивидуального прогнозирования метод оптимальной классификации по одному признаку.
1.Теория статистической классификации.
При индивидуальном прогнозировании по признакам с классификацией задача состоит в разделении исследуемой совокупности объектов и изделий на классы и нет необходимости в оценке конкретного значения прогнозируемого параметра . В большинстве практических случаев в том числе и при прогнозировании качества изделий число классов равно 2 , так бывает , например , когда исследуемую совокупность необходимо по заданному правилу разделить на класс годных и дефектных изделий . Рассмотрим решение задачи индивидуального прогнозирования методами теории статистической классификации для чего нужно располагать условными многомерными плотностями распределения признаков для каждого класса . Задача заключается в отыскании способа принятия оптимального решения о принадлежности проверяемого экземпляра к тому или иному классу в условиях неопределенности то есть в условиях действия случайных факторов которые маскирует связь между признаками и классом экземпляра .
Условимся , что проверяемый экземпляр принадлежит классу K1 . Если значение прогнозируемого параметра y к моменту времени  ,будет больше некоторого граничного значения ,
,будет больше некоторого граничного значения , 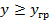 . Будем считать такие изделия годными .Если
. Будем считать такие изделия годными .Если 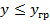 экземпляр принадлежит к классу K2 – дефектным . Зная плотность
экземпляр принадлежит к классу K2 – дефектным . Зная плотность 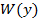 прогнозируемого параметра на момент времени
прогнозируемого параметра на момент времени  можно определить априорные вероятности принадлежности какого – либо экземпляра к классу К1 .
можно определить априорные вероятности принадлежности какого – либо экземпляра к классу К1 .
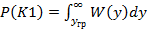 ( 1 )
( 1 )
и к классу К2
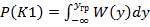 ( 2 )
( 2 )
Определение вероятностей принадлежности какого – либо экземпляра к классу К1 и К2 по выражениям ( 1 ) и ( 2 ) дает представления лишь о свойствах всего ансамбля изделий . Это не индивидуальное прогнозирование так как здесь не используется информация об индивидуальных особенностях 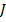 – го экземпляра ( то есть о значениях его признаков ) .
– го экземпляра ( то есть о значениях его признаков ) .
Пусть начальное состояние изделия характеризуется К – признаками каждый из которых является случайной величиной . Совокупность К случайных величин обозначим 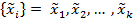 . По конкретным значениям признаков
. По конкретным значениям признаков 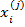
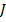 – го экземпляра необходимо принимать решения об отнесении этого экземпляра к классу К1 или К2 . В таком виде задачу целесообразно ставить лишь в том случае когда между классом которому принадлежит
– го экземпляра необходимо принимать решения об отнесении этого экземпляра к классу К1 или К2 . В таком виде задачу целесообразно ставить лишь в том случае когда между классом которому принадлежит 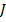 – ый экземпляр и значений его признаков существует какая – либо связь . Если эта связь выражается в виде жесткой функциональной зависимости то для определения принадлежности экземпляра к тому или иному экземпляру класса необходимо провести расчет по определенной формуле . Задача прогнозирования представляет наличие вероятностных связей между классом и признаками
– ый экземпляр и значений его признаков существует какая – либо связь . Если эта связь выражается в виде жесткой функциональной зависимости то для определения принадлежности экземпляра к тому или иному экземпляру класса необходимо провести расчет по определенной формуле . Задача прогнозирования представляет наличие вероятностных связей между классом и признаками 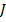 – го экземпляра . Степень тесноты этой связи полностью определяется видом условных совместных плотностей распределения признаков
– го экземпляра . Степень тесноты этой связи полностью определяется видом условных совместных плотностей распределения признаков 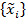 при условии что экземпляр принадлежит классу К1 :
при условии что экземпляр принадлежит классу К1 :
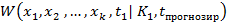
и к классу К2 :
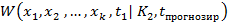
Для простоты записи будем их обозначать как :
 и
и  эти плотности могут быть получены с соответствующей обработкой результатов эксперимента . Совместной плотностью
эти плотности могут быть получены с соответствующей обработкой результатов эксперимента . Совместной плотностью 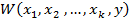 они связаны соотношениями :
они связаны соотношениями :
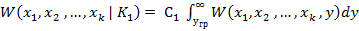 ( 3 )
( 3 )
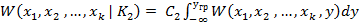 ( 4 )
( 4 )
Где :
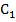 и
и 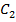 нормирующие коэффициенты :
нормирующие коэффициенты :
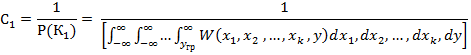
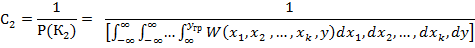
2.Вероятность принятия ошибочных решений при оптимальной классификации .
Принятие решения об отнесению экземпляра к классу К1 или К2 основано на вероятностных моделях , по – этому существует вероятность принятия ошибочных решений . Она заключается в переименование класса какого – либо экземпляра . Например , годный экземпляр ( К1) в соответствии с решением могут отнести к дефектным ( К2) или наоборот .
Следует оценить вероятность ошибки решений.
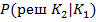 – условная вероятность принятия решения об отнесения экземпляра к классу К2 при условии что он фактически принадлежит классу К1.
– условная вероятность принятия решения об отнесения экземпляра к классу К2 при условии что он фактически принадлежит классу К1.
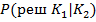 – условная вероятность принятия решения об отнесении экземпляра к классу К1 при условии что он фактически принадлежит классу К2
– условная вероятность принятия решения об отнесении экземпляра к классу К1 при условии что он фактически принадлежит классу К2
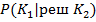 – условная вероятность того что экземпляр является годным ( К1 ) при условии что принято решение считать его дефектным ( К2 ) .
– условная вероятность того что экземпляр является годным ( К1 ) при условии что принято решение считать его дефектным ( К2 ) .
Это вероятность определяет на сколько рискует изготовитель когда верит прогнозировании , ее называют риском изготовителя .
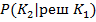 – условная вероятность того что экземпляр в действительности принадлежит классу К2 ( дефектным ) при условии что принято решение считать его годным ( К1 ) .
– условная вероятность того что экземпляр в действительности принадлежит классу К2 ( дефектным ) при условии что принято решение считать его годным ( К1 ) .
Эта вероятность определяет на сколько рискует потребитель , ее называют риском потребителя.
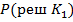 – априорная вероятность принятия решения об отнесении его к классу К1 , вероятность принятия решения об отнесения к годным любого наугад взятого экземпляра.
– априорная вероятность принятия решения об отнесении его к классу К1 , вероятность принятия решения об отнесения к годным любого наугад взятого экземпляра.
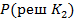 – априорная вероятность принятия решения об отнесении его к классу К2 , вероятность принятия решения об отнесения к дефектним любого наугад взятого экземпляра.
– априорная вероятность принятия решения об отнесении его к классу К2 , вероятность принятия решения об отнесения к дефектним любого наугад взятого экземпляра.
Вероятность ошибки в переименование классов экземпляра из К1 в К2 , то есть вероятность того что годный экземпляр ( К1 ) и относительно него принято решение об отнесении к К2 равна :
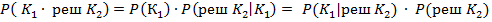 ( 5 )
( 5 )
Аналогично вероятность ошибки в переименовании класса экземпляра из К2 в К1 , то есть вероятность отнесения дефектного экземпляра к годным равна :
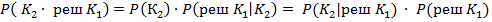 ( 6 )
( 6 )
3.Критерий Байеса. Отношение правдоподобия
Ошибочное решения всегда приводят к некоторым потерям . Обозначим потери связанные с переименование класса экземпляра из К1 в К2 то есть цену такого переименования 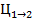 , а цену переименования из К2 в К1
, а цену переименования из К2 в К1 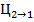 , тогда величина средних потерь при многократном распознавании будет равна с учетом выражений ( 5 ) и ( 6 ) :
, тогда величина средних потерь при многократном распознавании будет равна с учетом выражений ( 5 ) и ( 6 ) :
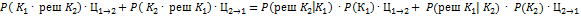 ( 7 )
( 7 )
В качества критерия оптимальности естественно взять min среднего риска
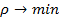 ( 8 )
( 8 )
Это наиболее распространенный критерий – критерий Байеса .В выражении ( 7 ) вероятности 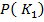 и
и 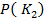 известны и они не зависят от процедуры прогнозирования так как их величина определяется фактической долей годных и дефектных экземпляров среди изделий данного типа .
известны и они не зависят от процедуры прогнозирования так как их величина определяется фактической долей годных и дефектных экземпляров среди изделий данного типа .
--------------------------------------------------------------------------------------------------------------14.10.11
Минимизация среднего риска может быть достигнута путем изменения вероятностей 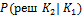 и
и 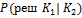 . Эти вероятности могут быть найдены по известным условным совместным плотностям распределения признаков ( 3 ) , ( 4 ) . Действительно:
. Эти вероятности могут быть найдены по известным условным совместным плотностям распределения признаков ( 3 ) , ( 4 ) . Действительно:
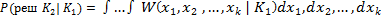 ( 9 )
( 9 )