Теорема Остроградского-Гаусса
Есть пространство, в котором задано векторное поле 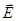 . Оно разбивается на площадки. Пусть определен вектор
. Оно разбивается на площадки. Пусть определен вектор 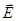 . Саму площадку будем рассматривать, как направленный участок площади.
. Саму площадку будем рассматривать, как направленный участок площади.
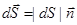
где 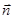 – это нормаль. Назовем элементарным потоком вектора
– это нормаль. Назовем элементарным потоком вектора 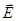 через площадку dS скалярное произведение:
через площадку dS скалярное произведение:
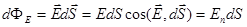
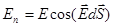
если мы окружили заряд замкнутой поверхностью, т.е. заряды находятся в объеме, образующем поверхность. Площадка 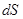 видна под телесным углом dW, если взять полны поток:
видна под телесным углом dW, если взять полны поток:
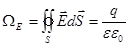 - это полный поток вектора
- это полный поток вектора 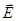 через замкнутую поверхность S. Поток численно равен заряду, заключенному в данную замкнутую поверхность.
через замкнутую поверхность S. Поток численно равен заряду, заключенному в данную замкнутую поверхность.
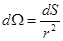
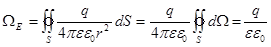
где 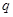 – это алгебраическая сумма всех зарядов, окруженных замкнутой поверхностью
– это алгебраическая сумма всех зарядов, окруженных замкнутой поверхностью 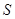 .
.
Энергия – способность к совершению работы. Потенциал(  ) - энергетическая характеристика любой точки поля. Рассматривается потенциальная энергия зарядов. Потенциальная энергия расходуется посредством совершения работы.
) - энергетическая характеристика любой точки поля. Рассматривается потенциальная энергия зарядов. Потенциальная энергия расходуется посредством совершения работы.
При вычислении потенциальной энергии единичного заряда берется работа по перемещению этого заряда из данной точки на бесконечность. Отношение этой работы к единичному заряду называется потенциалом в данной точке поля. Иными словами:
Потенциал – работа по перемещению единичного заряда из данной точки на бесконечность.
Для сравнения потенциалов различных точек нужно взять какую-либо точку отсчета. Реально можно измерить разность потенциалов или работу между двумя точками поля. За основу определения можно взять линейный интеграл по 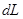 . На практике потенциал Земли принимают равным нулю.
. На практике потенциал Земли принимают равным нулю.
Связь потенциала(j) и напряженности(E)
Различают два вида полей: потенциальные и вихревые поля. Если работа по замкнутому пути равна нулю, то поле потенциальное. Форма пути не играет роли. Пример: гравитационное и электростатическое поля (подтверждено опытами). Если же такая работа не равна нулю, то поле называется вихревым. Пример: магнитное поле. Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом – энергетической характеристики поля.
В потенциальных полях работа равна:
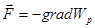 ;
;
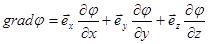 .
.
Градиент скалярной величины – это вектор.
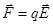 ;
;
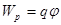 ;
;
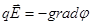 ,
,
откуда:
j= 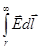 ,
, 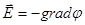 или
или 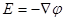 .
.
Т.е. напряженность 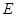 поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности
поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности 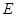 поля направлен в сторону убывания потенциала.
поля направлен в сторону убывания потенциала.
Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал имеет одно и тоже значение.
Если поле создается точечным зарядом, то его потенциал равен: 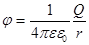 . Таким образом эквипотенциальные поверхности в данном случае – концентрические сферы. Линии напряженности всегда нормальны эквипотенциальным поверхностям, т.к. работа по перемещению заряженного тела по эквипотенциальной поверхности равна нулю.
. Таким образом эквипотенциальные поверхности в данном случае – концентрические сферы. Линии напряженности всегда нормальны эквипотенциальным поверхностям, т.к. работа по перемещению заряженного тела по эквипотенциальной поверхности равна нулю.
