Проверка гипотезы о значимости найденного уравнения ПФ
Кейс-задача 2
Задание выполняется на лабораторной работе № 2: Нахождение параметров нелинейной регрессии. Оценка качества оцененных регрессионных уравнений. Интерпретация результатов нелинейного регрессионного моделирования
Базовый уровень:
Построить нелинейную регрессионную модель, отражающую зависимость одного экономического или социального фактора от другого. Выборка должна включать не менее 30 наблюдений. В качестве метода нахождения оценок неизвестных параметров регрессионной модели использовать метод итерационного оценивания, указав вид функции потерь и критерий сходимости..
Проанализировать адекватность построенного нелинейного регрессионного уравнения:
оценить качество подгонки уравнения под реальные данные.
проверить различные гипотезы относительно параметров нелинейного уравнения.
проверить условия для получения состоятельных, несмещенных, эффективных оценок коэффициентов модели нелинейной регрессии.
провести содержательный анализ модели и скорректировать модель, если это необходимо.
Оформить результаты в виде отчета по лабораторной работе.
В качестве информационных средств выполнения задания рекомендуется использовать Statistica, Eviews, R.
Повышенный уровень:Применить метод наименьших квадратов для оценки параметров нелинейной регрессии, приведенной к линейному виду. Проверить условия для коэффициентов модели с помощью теста Вальда.
Дополнительное задание (необязательное):Протестировать нелинейную регрессию на возможные функциональные изменения.
Результатом выполнения кейс-задания является отчет по лабораторной работе № 2. К отчету предъявляются следующие требования:
Четкое формулирование поставленной цели исследования (например: цель: Определить какое влияние на объем производства за 2015 год оказывают такие факторы как объем основных средств, численность работников предприятия)
Формулирование задач, решение которых необходимо для достижения поставленной цели.
Описание в виде пунктов, тех действий, которые требуются для решения поставленных задач. Все рисунки и таблицы последовательно нумеруются и описываются. Каждый пункт решения поставленных задач сопровождается анализом принятого решения. При проведении статистических тестов на определение статистической значимости модели в целом и отдельных ее параметров, обязательно выписывается нулевая и альтернативная гипотеза, указывается критическая область отказа от нулевой гипотезы в пользу альтернативной.
В заключении выписывается уравнение нелинейной регрессии и проводится его содержательный анализ на основе расчета средних и маржинальных значений, частных и общих коэффициентов эластичности, предельной технологической нормы замены одного независимого фактора другим.
Критерии оценки:
- Максимальный балл, который бакалавр может получить за выполнение задания -10 баллов, причем из них 4 балла за защиту отчета по выполнению задания.
- Нахождение параметров нелинейной регрессии. Оценка качества оцененных регрессионных уравнений. Интерпретация результатов нелинейного регрессионного моделирования
- Осваивается умение строить адекватные нелинейные регрессионные линейные уравнения, проводить их мониторинг и давать качественную интерпретацию результатов моделирования на основе расчета коэффициентов эластичностей и показателей предельной технологической нормы замены.
- Прежде чем воспользоваться модулем нелинейного оценивания, нужно ввести данные с клавиатуры в пакете STATISTICA, предварительно дав название каждому параметру. По меню «Statistics» выбираем режим Advanced Linear/ Nonelinear Models (Дополнительные линейные / нелинейные модели), из предложенного списка выбираем Nonelinear Estimation (Нелинейная оценка) (рис. 22).
-
- 
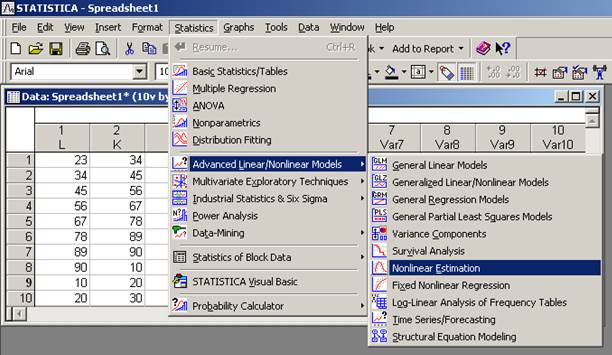
- Рисунок 22 - Переход в модуль нелинейного оценивания
- При выборе появляется диалоговое окно выбора различных режимов нелинейного оценивания:
- User-specified regression least squares (Оцененная пользователем специальная регрессия с методом наименьших квадратов);
- User-specified regression, Custom loss function (Оцененная пользователем специальная регрессия с заданием функции потерь);
- Quick Logit regression (Быстрая логистическая регрессия);
- Quick Probit regression (Быстрая нормальная регрессия);
- Exponential growth regression (Модель экспоненциального роста);
- Piecewise linear regression (Кусочно-линейная регрессия);
- Функциональная часть появившегося диалогового окна Nonlinear Estimation… (рис.23) содержит кнопки: OK, Cancel, Options, Open Data. А также кнопки, предназначенные для отбора наблюдений 
и придания некоторым наблюдениям особого веса 
. Из предложенного списка функций, выбираем User-specified regression, custom loss function (задаваемая пользователем регрессия, функция потерь пользователя).
- 
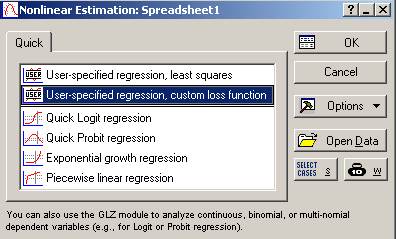
- Рисунок 23 - Подмодули модуля нелинейного оценивания
-
- В правой части окошка (рис. 24), появившегося после выбора режима User-specified regression, custom loss function, находятся следующие кнопки: ОК; Cancel (Отмен); Options (Параметры); Open Data (Открыть данные); Analysis/Graph Selection Conditions (Условия выбора случая анализа/графа); Analysis/Graph Case Weights (Весовые коэффициенты случая); MD deletion (Методы восполнения пропущенных данных) включает в себя 2 режима: Пропуск (Casewise) и Замена средним (Mean substitution).
- В высветившемся окне, нажав на кнопку Function to be estimated& loss function (функция, которая будет оценена & функция потерь), получим (Рис. 25).
- 
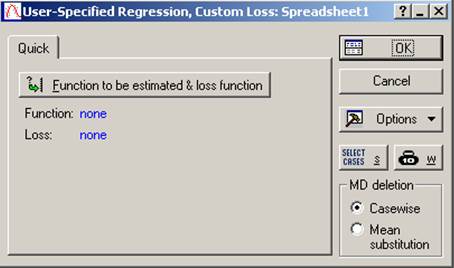
- Рисунок 24 – Диалоговое окно задаваемой пользователем регрессии с задаваемой, функцией потерь.
- 
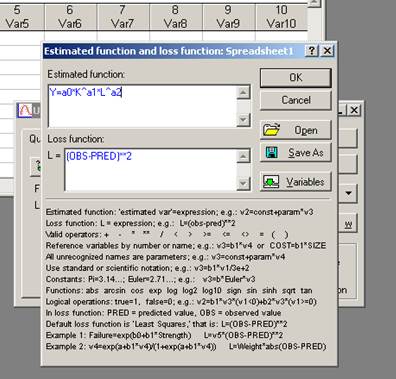
- Рисунок 25 – Диалоговое окно для задания пользователем функции регрессии и функции потерь.
- В окне Estimated function (оцениваемая функция), вводим формулу, с помощью которой имеется возможность оценки параметров и их стандартных ошибок. В окне Loss function задается вид функции потерь, которая буде минимизироваться в ходе проведения процедур оцени параметров. В нашем случае предложена функция потерь как квадрат разности между фактическими и расчетными значениями зависимой переменной (OBS-PRED)2. Здесь дана для примера формула производственной функции Коба-Дугласа, имеющая общий вид: Y=a0*K^a1*L^a2. (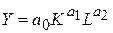 
), где K – объем капитала, L – объем труда, Y – объем производства.
- Нажав на кнопку OK, получим окно Model Estimation (Оценивание модели) (рис. 26), где указывается Number of parameters to be estimated (количество параметров оценивания), Loss function (вид функции потерь), Dependent variable (зависимая переменная), Independent variables (независимые переменные), number of valid cases (количество фактических действий).
- В окне содержится 3 вкладки- Quick (быстрый анализ), Advanced(расширенный анализ), Review (Просмотр); во вкладке Quick (быстрый) в прокручиваемом списке выбираем один из Estimation method (методов нелинейного оценивания)- Quasi-Newton,(Квази-Ньютона), Simplex (Симплекс), Simplex and quasi-Newton(Симплекс и Квази-Ньютона ), Hooke-Jeeves(Хука-Дживса) pattern moves, Hooke-Jeeves and quasi-Newton(Хука-Дживса и Квази-Ньютона), Rosenbrock pattern search. (Розенброкка). Все перечисленные методы относятся к методам оценки параметров с использованием итеративных процедур.
- Для примера выберем метод нелинейного оценивания Квази-Ньютона.
- 
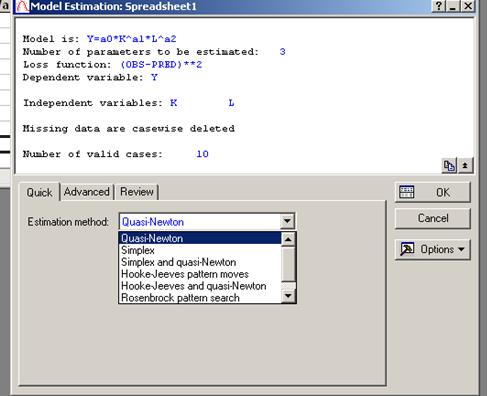
- Рисунок 26 – Выбор метода итерационного оценивания.
- После открытия вкладки Advanced (расширенный), появится окно (рис. 27), где требуется ввести Maximum numbers of iterations (Максимальное число итераций) и convergence criterion (критерий сходимости процесса). С помощью кнопок Start values и Initial step sizes можно определить начальные параметры итеративных процедур и шаг итераций соответственно.
- 
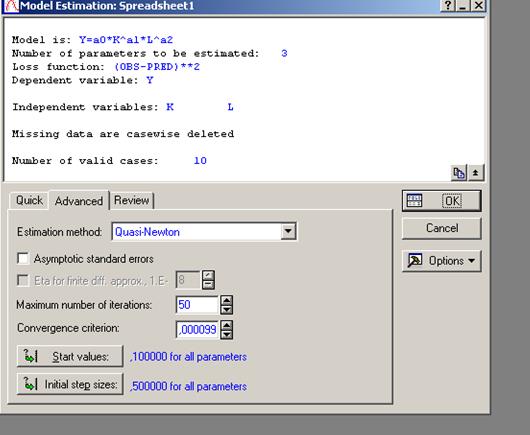
- Рисунок 27 – Задания парметров итерационого оценивания коэффициентов модели.
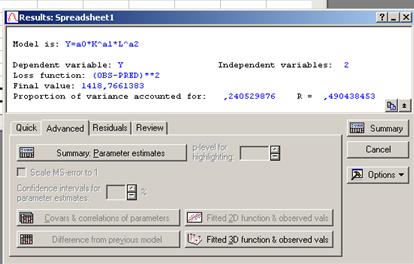
- После нажатия кнопки ОК появляется диалоговое окно результатов оценки Results (рис. 28). Вкладка Quick (быстрый анализ) содержит следующие функциональные кнопки: Summary Parameter estimates (Итог оценки параметров), Observed, predicted, residual values (фактические, предсказанные, остаточные значения переменной), Fitted 3D function & observed values (подобранная 3D функция & фактические (исходные) значения). В информационной части окна (рис. 28) содержится информация: Dependent variable (зависимая переменная), Loss function (функция потерь), Final value (последнее значение, полученное после проведения итеративных процедур оценки), Proportion of variance accounted for.. (доля дисперсии приходится на..) (аналог индекса детерминации), Independent variables (зависимая переменная), а также R- коэффициент корреляции, показывающий взаимосвязь переменных.
- 
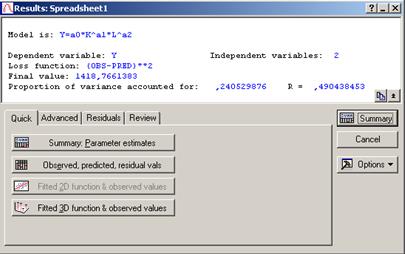
- Рисунок 28– Диалоговое окно результатов оценивания.
- Нажав на кнопку Summary Parameter estimates (Итог оценки параметров), получим значения оцениваемых параметров (в рассматриваемом примере а0, а1 , а2) рисунок 29.
- 
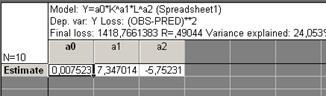
- Рисунок 29– Результаты оценок коэффициентов модели.
- Итак, уравнение будет иметь вид: Y=0,0075*K^7,347*L^(-5,752).
- Или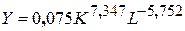 
.
- Для мониторинга построенной модели требуется проанализировать ее остатки на соответствие случайности, нормальности распределения и нулевого математического ожидания. Вкладка диалогового окна результатов Residuals(Остатки) содержит следующие функции (рис. 30): Observed, predicted, residual values (фактические, предсказанные, остаточные значения), Normal probability plot of residuals,(построение графика соответствия остатков нормальному распределению), save predicted and residual values (сохранить расчетные и остаточные значения), histogram of residuals (гистограмма остатков), half-normal probability plot (построение графика соответствия остатков полу-нормальному распределению), Predicted observed values (график расчетных значений относительно фактических), Predicted residual values (график расчетных значений относительно остатков).
- 
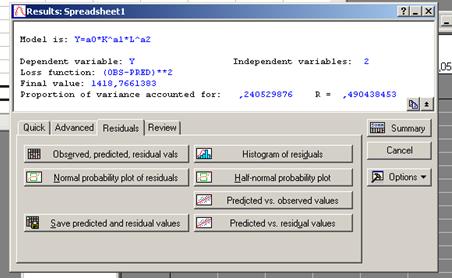
- Рисунок 30– Диалоговое окно для анализа остатков модели.
- Используя кнопку Observed, predicted, residual values (фактические, расчетные, остаточные значения), получим таблицу соответствующих значений (рис. 31).
- 
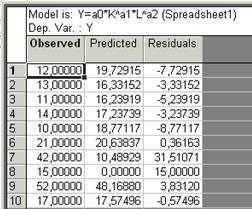
- Рисунок 31– Фактические, расчетные, остаточные значения модели регрессии.
- Для мониторинга модели следует проанализировать остатки модели на соответсвие нормальному распределению. Для этого можно проанализировать график Frequency distribution residuals (плотности распределения остатков), используя кнопку histogram of residuals (гистограмма остатков) в окне анализа остатков, рис. 32:
- 
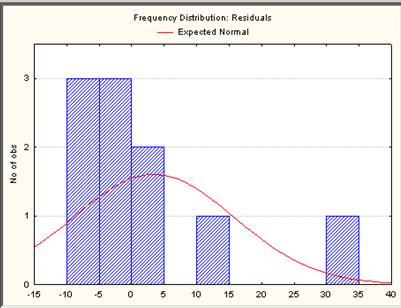
- Рисунок 32– График плотности распределения остатков модели.
- Также можно проанализировать график нормальной плотности остатков модели. С помощью функции Normal probability plot of residuals, получим график нормальной плотности (рис. 33):
- 
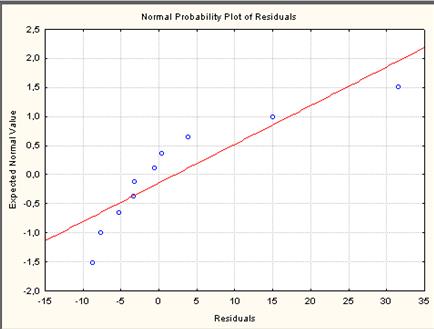
- Рисунок 33– График нормальной плотности остатков модели.
- По графикам рисунокв 32 и 33 можно сделать вывод, что распределение остатков оцененной модели далеко от нормального.
- Также мониторинг качества построенной модели можно проводить на основе анализа различных графиков остатков. Используя функцию Predicted observed values получим график расчетных значений относительно фактических (рисунок 34):
- 
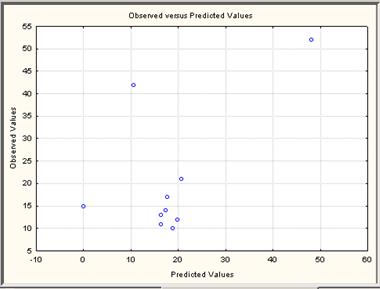
- Рисунок 34–Гграфик расчетных значений относительно фактических.
- Используя функцию Predicted residual values получим график расчетных значений относительно остатков (рисунок 35).
- 
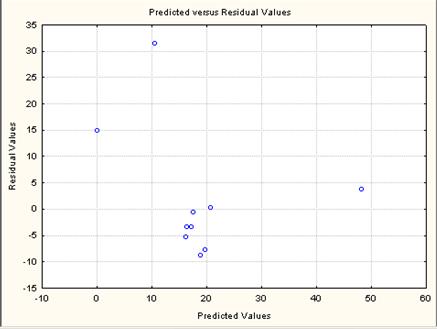
- Рисунок 35– График расчетных значений относительно остатков.
- Анализ графиков на рисунках 34 и 35 показывает, что в расположении точек не наблюдается направленная связь, и можно сделать вывод о независимости и случайности остаточной компоненты модели.
- В диалоговом окне результатов (рис. 36) заходим во вкладку Advanced (Расширенный анализ) выбираем функцию: Flitted 3D function & observed values (эмпирическая 3D функция & измеренные значения). Это позволит построить 3D модель оцененной регрессии.
- 
- Рисунок 36– Диалоговое окно для построения 3D модели оцененной регрессии.
- Получаем трехмерный график оцененной функции (рисунок 37). Как видим,график не построился в виде гладкой поверхности, это связано с тем, что качество оценки функции было неудовлетворительное (R2 = 0,2):
-
- 
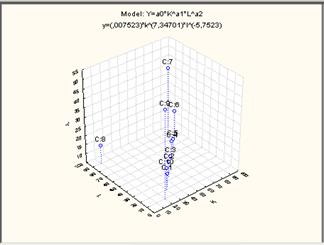
- Рисунок 37– Трехмерный график оцененной функции.
- В диалоговом окне, во вкладке Review (просмотр) (рисунок 38), содержатся следующие операции: Means & standard deviations (среднее значение и среднеквадратичное отклонение), Matrix plot for all variables (построение матрицы для всех значений), Box & whisker plot for all variables (точечное вычерчивание для всех значений). Данные операции позволяют провести более детальный анализ остатков модели.
- 
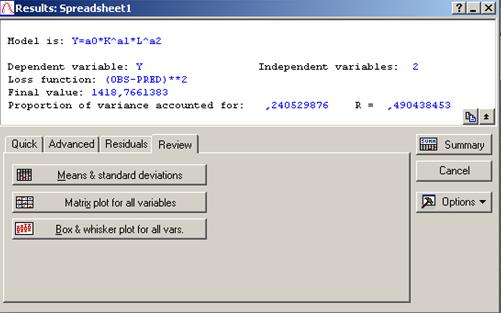
- Рисунок 38– Диалоговое окно для просмотра остатков модели в различных режимах.
Расчет коэффициентов эластичности, маржинальных и средних величин, показателей предельной технологической нормы замены для уравнений нелинейной регрессии Осваивается умение проводить интерпретацию результатов нелинейного регрессионного моделирования на основе расчета специальных показателей. Также осваивается умение проводить проверку адекватности найденной нелинейной регрессии .
Оценка и расчет параметров производственных функций
1. Линейная производственная функция:
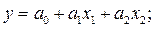
где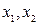 
– ресурсы производства, 
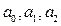– оцениваемые параметры.
2. Производственная функция Кобба-Дугласа (ПФКД) имеет вид:
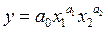
где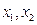 
– ресурсы производства, 
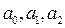– оцениваемые параметры, причем 
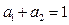и 
.
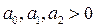Пример ПФКД:
,
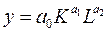где К – капитал, L – труд, y– объем производства,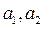 
– оцениваемые параметры, соответственно выражающие эластичность по капиталу и труду. В случае эластичности производства 
, 
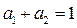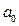– оцениваемый параметр, отвечающий за общий прирост производства (например: объем производства за счет НТП).
Можно от мультипликативной формы записи производственной функции Кобба-Дугласа перейти к аддитивной линейной модели с помощью логарифмирования.
Пусть производственная функция имеет вид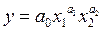 
. Прологарифмируем обе части выражения и получим 
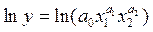. В силу свойств логарифма 
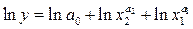или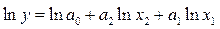 
. Обозначим 
, 
, 
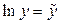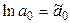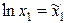и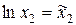 
. Тогда производственная функция примет вид линейной функции:
.
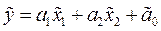Можно выполнить и обратный переход от аддитивной формы записи модели производственной функции к мультипликативной с помощью процедуры потенцирования.
Можно также понизить число факторов в производственной функции.
Рассмотрим двухфакторную производственную функцию следующего вида: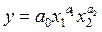 
, где 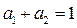. Разделим ее на L≠0 и получим: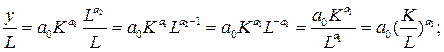 
Таким образом, имеем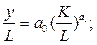 
Введем обозначения: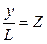 
– производительность труда; 
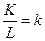–капиталовооруженность труда, тогда:
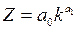
Таким образом, получили из двухфакторной функции однофакторную производственную функцию.
При условии, что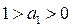 
следует, что производительность труда Z растет медленнее его капиталовооруженности.
Существуют также следующие обозначения:
Y/K – производительность капитала (капиталоотдача);
K/Y – капиталоемкость производства;
L/Y – трудоемкость производства.
Проверка адекватности производственной функции
Под адекватность модели понимают соответствие её реальному моделируемому процессу.
Адекватность модели, как правило, проверяется в три этапа:
1. анализируются показатели качества подгонки модели;
2. проверяются гипотезы относительно значимости как уравнения модели в целом, так и ее параметров в отдельности;
3. проверяются условия получения достоверных оценок параметров модели.
Показатели качества подгонки моделей характеризуют, насколько качественно модель описывает исходные реальные данные.
1. Индекс корреляции описывает тесноту корреляционной зависимости между фактором и результатом и определяется как:
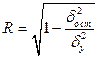, (9)
здесь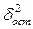 
– это дисперсия, объясненная уравнением производственной функции 
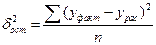, n – объем выборки, 
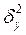– общая дисперсия 
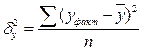, где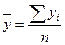 
.
Величина этого показателя находится в пределах от 0 до 1. Чем ближе индекс детерминации к единице, тем теснее связь между факторами. В случае, когда R=1, между рассматриваемыми в уравнении производственной функции факторами существует строгая функциональная зависимость.
2. Индекс детерминации R2 определяет качество подгонки уравнения под реальные данные. Чем ближе данный показатель к единице, тем лучше качество подгонки. Определяется как:
3. Средняя ошибка аппроксимации, еще один показатель позволяющий оценить качество подгонки модели в процентном отношении. Определяется по формуле:
.
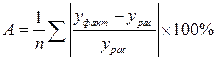Если ошибка аппроксимации находится в пределах 5-7%, то это свидетельствует о хорошем качестве подгонки модели под исходные данные.
Проверка гипотезы о значимости нелинейной модели производственной функции
Выдвигают нулевую гипотезу Н0 о несущественности построенного уравнения для производственной функции. Соответственно альтернативная гипотеза Н1, наоборотпредполагает его значимость. Статистический критерий рассчитывают, согласно формуле:
,
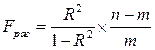здесь R2 – индекс детерминации модели, n – общее число наблюдений, m – число оцениваемых параметров.
По таблице критических значений распределения Фишера-Снедекора на заданном уровне значимости α определяют Fтабличное, и сравнивают полученные расчетное и табличное значения. Если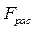 
> 
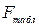, то гипотезу Н0 о несущественности найденной модели производственной функции отклоняют на заданном уровне значимости и принимают альтернативную гипотезу о значимости производственной функции.
Пример проверки адекватности производственной функции
Расчет средней ошибки аппроксимации в производится в Excel.
Таблица 1 Промежуточные расчеты
| Y факт | Y расч | (1)-(2) | (3)/(2) | ABS((3)/(2)) |
| 0,18138176 | 0,18138176 | |||
| -194496 | -0,19387117 | 0,193871166 | ||
| 0,1402792 | 0,1402792 | |||
| 0,013516522 | 0,013516522 | |||
| -32021 | -0,04839289 | 0,048392894 | ||
| 0,323367026 | 0,323367026 | |||
| 0,255346885 | 0,255346885 | |||
| -98027 | -0,14881192 | 0,148811922 | ||
| 0,079350034 | 0,079350034 | |||
| 0,042059677 | 0,042059677 | |||
| -6098 | -0,01527327 | 0,015273273 | ||
| 0,000908675 | 0,000908675 | |||
| -141369 | -0,28753796 | 0,287537959 | ||
| -46342 | -0,11690711 | 0,116907106 | ||
| -53725 | -0,14310212 | 0,143102124 | ||
| 0,054822241 | 0,054822241 | |||
| -11652 | -0,03559494 | 0,035594942 | ||
| -6332 | -0,02017774 | 0,020177743 | ||
| 0,004668069 | 0,004668069 | |||
| -48840 | -0,16042627 | 0,160426272 | ||
| Сумма | 2,265795489 |
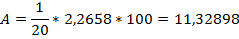
Так как А=11,329>7%, следовательно качество подгонки исходных данных под уравнение ПФКД слабое.
Проверка гипотезы о значимости найденного уравнения ПФ
Выдвигается гипотеза Н0 о несущественности найденного уравнения ПФ. Выдвигается альтернативная гипотеза Н1 о значимости уравнения ПФ. Далее рассчитывается:
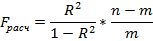
Необходимо сравнить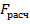 
и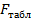 
. Последнее определяется при помощи модуля Probability Calculator (Вероятностный калькулятор) пакета Statistica поле Distributions (Распределения) (рис. 51).
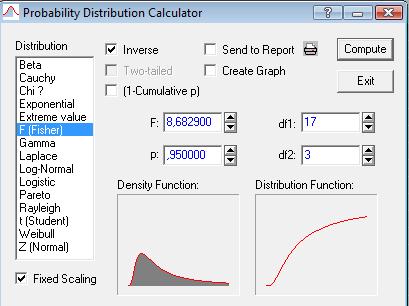
Рисунок 51. Определение Fтабл.
В качестве распределения выбираем распределение Фишера со степенями свободы df1 и df2.
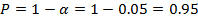
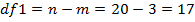
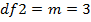
Таким образом,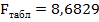 
. Найдем 
.
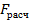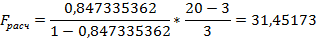
Если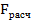 
> 
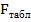, то гипотеза Н0 отвергается на заданном уровне значимости и считают, что уравнение ПФ значимо с вероятностью p=0.95.
Так как 31,45173>8,6829, значит, гипотеза Н0 отвергается и уравнение считается значимым на заданном уровне значимости 0,95.