Задачи и примеры их решения
 |
| Рис.1 |
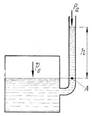
Задача 1. В закрытом сосуде находится вода, глубина наполнения сосуда  Давление на поверхности
Давление на поверхности  . Определить высоту поднятия воды в открытой трубке над уровнем в сосуде (давление в открытом конце трубки атмосферное); полное и избыточное давление у дна сосуда. Построить эпюры гидростатического давления на плоскую боковую стенку в закрытом сосуде (рис.1).
. Определить высоту поднятия воды в открытой трубке над уровнем в сосуде (давление в открытом конце трубки атмосферное); полное и избыточное давление у дна сосуда. Построить эпюры гидростатического давления на плоскую боковую стенку в закрытом сосуде (рис.1).
Решение задачи 1:
Примем 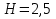 м,
м, 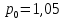 атм,
атм, 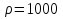 кг/м3?
кг/м3? 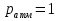 атм.
атм.
Так как жидкость находится в покое, то гидростатическое давление в трубке на глубине равно давлению на поверхности жидкости в сосуде 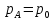 и определяется из основного уравнения гидростатики следующим образом:
и определяется из основного уравнения гидростатики следующим образом:
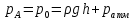
откуда высота поднятия воды в открытой трубке над уровнем в сосуде:
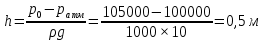
Для определения полного (или абсолютного) давления у дна сосуда воспользуемся основным уравнением гидростатики:
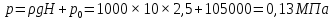
Избыточное (или манометрическое) давление есть превышение полного (абсолютного) давления над атмосферным, то есть:
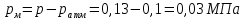
Эпюра дает графическое изображение изменения гидростатического давления вдоль поверхности. Так как избыточное гидростатическое давление в точке боковой стенки закрытого резервуара у поверхности равно 0,05 атм, а в точке у дна - 0,3 атм, для построения эпюры давления на эту стенку необходимо восстановить перпендикуляры в удобном масштабе к точкам у поверхности и дна, соединить концы перпендикуляров прямой линией, т. к. давление изменяется с глубиной линейно и направлено по нормали к площадке действия.
 |
| Рис. 2 |
Задача 2. На поршень одного из сообщающихся сосудов (рис.2), наполненных водой, действует сила 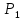 , а на поршень второго сосуда
, а на поршень второго сосуда 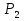 . Определить разность уровней жидкости в сосудах
. Определить разность уровней жидкости в сосудах 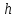 , если диаметр первого поршня
, если диаметр первого поршня 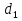 , второго поршня
, второго поршня 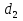 .
.
Решение задачи 2:
Примем 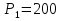 Н,
Н, 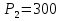 Н,
Н, 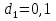 м,
м, 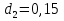 м.
м.
Давление на единицу площади на поверхности жидкости под первым поршнем
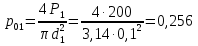 атм.
атм.
То же, на поверхности жидкости под вторым поршнем
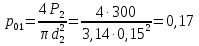 атм.
атм.
Гидростатическое давление во втором сосуде на глубине определяется по основному уравнению гидростатики 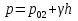 .
.
Так как жидкость находится в покое, можно записать 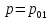 . Тогда
. Тогда 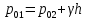 , откуда
, откуда
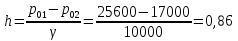 м,
м,
где 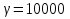 Н/м3 - объемный вес воды.
Н/м3 - объемный вес воды.
 |
| Рис. 3 |
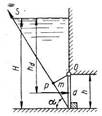
Задача 3. Донное отверстие плотины перекрывается плоским прямоугольным щитом (рис.3), шарнирно прикрепленным к телу плотины своей верхней кромкой. Определить, какое усилие нужно, приложить к тросу для открытия щита, если глубина погружения нижней кромки щита , высота щита , ширина щита 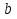 , угол между направлением троса и горизонтом
, угол между направлением троса и горизонтом 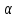 .
.
Решение задачи 3:
Примем 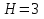 м,
м, 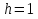 м,
м, 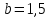 м,
м, 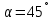 .
.
Давление воды на щит 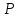 определяем по формуле
определяем по формуле 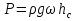 , где площадь щита
, где площадь щита 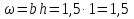 м2; глубина погружения центра тяжести щита
м2; глубина погружения центра тяжести щита 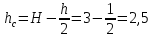 м.
м.
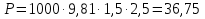 кН.
кН.
Глубину погружения центра давления щита находим по формуле:
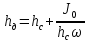 ,
,
где момент инерции площади щита
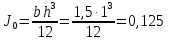 м4,
м4,
тогда
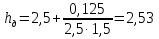 м.
м.
Усилие для открытия щита определится из равенства моментов 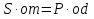 , откуда
, откуда
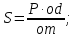
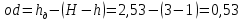 м;
м;
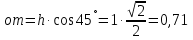 м,
м,
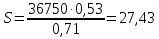 кН.
кН.
 |
| Рис. 4 |
Задача 4. В призматическом сосуде шириной установлена перегородка, имеющая в своей нижней части форму четверти цилиндрической поверхности с радиусом 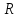 (рис.4). Определить суммарное давление воды на криволинейную часть перегородки, если глубина воды слева
(рис.4). Определить суммарное давление воды на криволинейную часть перегородки, если глубина воды слева 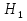 и справа
и справа 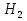 . Найти точку приложения равнодействующей давления воды.
. Найти точку приложения равнодействующей давления воды.
Решение задачи 4:
Примем 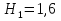 м,
м, 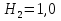 м,
м, 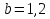 м,
м, 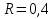 м.
м.
Горизонтальная составляющая давления воды слева
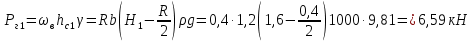 .
.
Горизонтальная составляющая давления воды справа
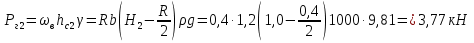 .
.
Вертикальная составляющая давления воды слева
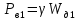 ,
,
где 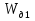 - объем тела давления,
- объем тела давления,
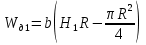 ,
,
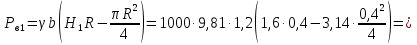
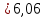 кН.
кН.
Вертикальная составляющая давления воды справа
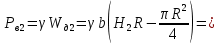
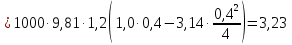 кН.
кН.
Суммарное давление воды
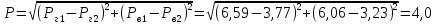 кН.
кН.
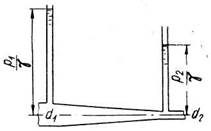
Суммарное давление воды направлено перпендикулярно к поверхности перегородки, поэтому линия ее действия должна пройти через центр О. Угол наклона линии действия суммарного давления к горизонту определяем из соотношения
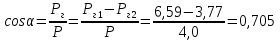 ; .
; .
Из центра О проводим линию под углом к горизонту. Точка пересечения этой линии с перегородкой является точкой приложения равнодействующей давления воды.
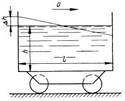
Задача 5. Призматический сосуд длиной  шириной заполнен водой на глубину (рис.5). Определить силы давления воды на переднюю и заднюю стенки сосуда при его горизонтальном перемещении с ускорением
шириной заполнен водой на глубину (рис.5). Определить силы давления воды на переднюю и заднюю стенки сосуда при его горизонтальном перемещении с ускорением 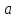 .
.
 |
| Рис. 5 |
Решение задачи 5:
Примем 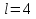 м,
м, 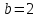 м,
м, 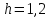 м,
м, 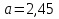 м/с2.
м/с2.
Понижение уровня воды у передней стенки и повышение уровня воды у задней стенки движущегося сосуда определяем по зависимости
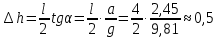 м.
м.
Глубина воды у передней стенки
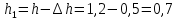 м.
м.
Глубина воды у задней стенки
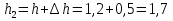 м.
м.
Сила давления воды на переднюю стенку
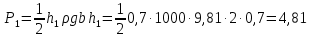 кН.
кН.
Сила давления воды на заднюю стенку
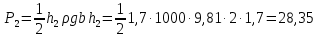 кН.
кН.
ДОМАШНЕЕ ЗАНИЕ ГИДРАВЛИКА
По вариантам
ВАРИАНТ 1
1. Определить скорость перемещения поршня в гидроцилиндре, если диаметр поршня равен d = 0,2 м, а объемная подача жидкости из напорной магистрали Q = 0,01 м3/с. Какое усилие можно получить на штоке поршня, если давление p в системе равно 2 МПа? Потери на трение и объемные потери не учитывать.
2. 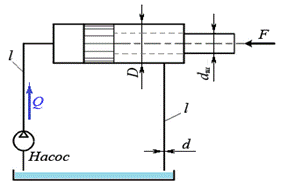 Определить расход жидкости, вытесняемой из штоковой области и скорость движения жидкости в отводящей линии, если известны:
Определить расход жидкости, вытесняемой из штоковой области и скорость движения жидкости в отводящей линии, если известны:
скорость поршня vП = 0,44 м/с.
диаметр трубопровода d= 0,012 м;
диаметр поршня D = 0,07 м;
Потери напора в местных сопротивлениях не учитывать.
ВАРИАНТ 2
1. После сжатия воды в цилиндре под поршнем давление в ней увеличилось на 3 кПа. Необходимо определить конечный объем V2 воды в цилиндре, если ее первоначальный объем составлял V1 = 2,55 л. Коэффициент объемного сжатия воды βV = 4,75 · 10-10 Па-1.
2. 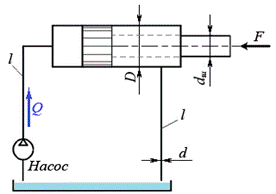 Определить режимы движения рабочей жидкости в питающей и отводящей линии изображенного на схеме гидропривода.
Определить режимы движения рабочей жидкости в питающей и отводящей линии изображенного на схеме гидропривода.
Исходные данные:
Скорость движения жидкости в питающей линии
v1 = 15,04 м/с, скорость движения жидкости в отводящей линии v2 = 10,08 м/с, вязкость жидкости v = 0,5×10-4, диаметр трубопроводов d = 0,012 м.
Критическое число Рейнольдса для рабочей жидкости равноReкр=2320
Потери напора в местных сопротивлениях и трубопроводах не учитывать.
ВАРИАНТ 3
1. 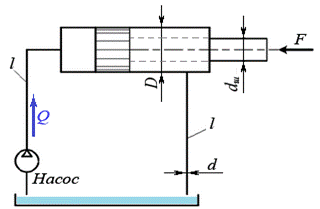 Определить скорость движения жидкости в подводящей линии и скорость поршня, если известны:
Определить скорость движения жидкости в подводящей линии и скорость поршня, если известны:
диаметр трубопровода d= 0,012 м;
диаметр поршня D = 0,07 м;
подача насоса Q = 1,7х10-3 м3/с.
Потери напора в местных сопротивлениях не учитывать.
2. Вода вытекает через отверстие в тонкой стенке в бак, имеющий объем V = 1,90 м2. Площадь отверстия S = 20 см2. Напор над центром отверстия Н1 = 0,90 м является постоянным. Коэффициент расхода отверстия μS = 0,62.
Определить время t наполнения бака водой.
