Гармонический анализ периодических колебаний

Выберем систему тригонометрических функций (3). Положив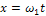

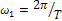( .- "круговая" частота) и задаваяпоследовательно значения 0,1,2,…N,…. получим следующую бесконечную, упорядоченную и полную систему функций

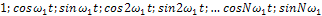(10)

ортогональных на любом отрезке длиной Т, например, 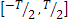. В этом легко убедиться, проверив выполнение соотношений (2) и установив, что 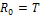при k=0 и 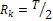при всех других k.

Поскольку в системе (10) каждому значению k соответствуют две функции (кроме k=0), принято записывать соответствующий ряд (4) в виде:

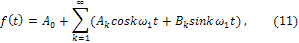
причем, как следует из вышесказанного, для однозначного представления заданной функции f(t) необходимо удовлетворение условий Дирихле и вычисление коэффициентов согласно общей формуле (6).

Так, если f(t) на отрезке 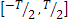, коэффициенты 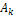(включая 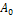), при косинусных, и B_K, при синусных оставляющих, определяют по формулам:

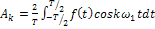
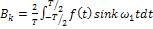(12)

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">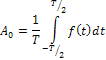

Размерность этих коэффициентов такая же, как у функции f(t). Представление (11) справедливо и для функции f(t), определенной при всех 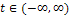, если свойства этой функций, проявившиеся на отрезке 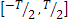, повторяется периодически с периодом Т. Иначе говоря, бесконечный ряд Фурье (12) однозначно представляет периодическую функцию, если в пределах периода Т она удовлетворяет условиям Дирихле, а коэффициенты определены по формулам (12).

Ряд (11) представляет колебание f(t) в виде суммы постоянной составляющей , косинусоидальных и синусоидальных колебаний с амплитудами и частотами , кратными основной частоте - частоте колебания f(t). В зависимости от номера К эти составляющие принято называть первой, второй, третьей и т.д. гармониками.

Если функцию f(t) удобнее описывать на отрезке [0;T] ,то при определении коэффициентов необходимо только изменить пределы интегрирования в формулах (12).

Очевидно, в ряд Фурье можно разложить не только функцию времени t, но и периодическую функцию любой другой переменной.

Практически часто применяют ряд Фурье в более компактной форме записи. Объединим попарно косинусные и синусные составляющие ряда (11)

+

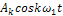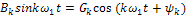
Преобразуя правую часть по известным формулам и приравнивая коэф­фициенты при синусах и косинусах, получаем

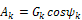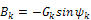; s w:space="720"/></w:sectPr></w:body></w:wordDocument>">

и, следовательно

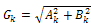
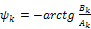
, (13)

Тогда ряд (11) примет вид:

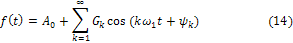
где k -той гармонике соответствует только одно слагаемое ряда с амплитудой и начальной фазой .

Важной для практических применений является также комплексная форма ряда Фурье. Для получения ее воспользуемся формулами Эйлера

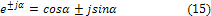
и представим действительную составляющую (k-тую гармонику) ря­да (14) в виде суммы двух комплексных функций переменнойt с номерамиkи -k

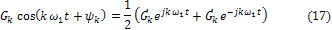
Где 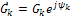- комплексная амплитуда;.

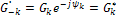- величина, комплексно сопряженная с .

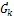Совокупность таких функций 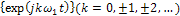образует полную систему, ортогональную на любом отрезке длиной Т, причем о учетом особенностей комплексных функций условия ортогональности принимают вид:

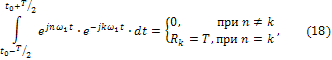
Где 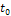- произвольный момент отсчета, определяющий середину отрезка ортогональности. Подставив (I7) в (14) и расширив границы измененияkв область отрицательных значений ( 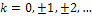), получим

ряд Фурье в комплексной форме:

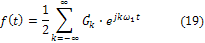
Причем 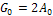. Отрицательные частоты 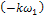введены здесь только для удобства записи, в действительности их нет.

Формулу для определения коэффициентов ряда найдем в результате умножения правой и левой частей (19) на 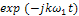и последующего интегрирования с учетом (18):

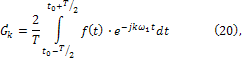
(k=0,±1,±2,...)

Она является модификацией общей формулы (6) для системы ортогональных функций, принимающих комплексные значения.

Формулы (19) и (20) называют парой преобразований Фурье - обратным и прямым соответственно. Прямое преобразование (20) позволяет найти комплексный спектр 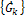, который содержит информацию о совокупности амплитуд 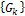(амплитудно-частотный спектр) и начальных фаз 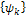(фазо-чаcтотный спектр) гармонических составляющих, образующих в сумме (14) или (19) функцию f(t). Для наглядности принято изображать амплитудно-частотный спектр в виде спектральной диаграммы (рис.1.в), где k -тую гармоническую составляющую изображают вертикальным отрезком, длина которого, (в некотором масштабе) равна амплитуде 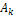, а местоположение на го­ризонтальной оси – частоте 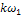этой составляющей. Фазо-частотный спектр при необходимости изображают аналогичным образом.

Итак, ряд Фурье, записанный в одной из трех форм (11), (14) и (19), представляет периодическое колебание f(t) в виде бесконечной суммы гармонических составляющих, амплитуды которых имеют конечные величины, а частоты принимают только дискретные значения 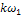. Поэтому спектр такого колебания называют дискретным или линейчатым. Причина этого в однородности функции f(t )и составляющих ряда Фурье - все они периодические функции, причем величина Т (длина отрезка ортогональности составлявших) является для всех периодом (не обязательно наименьшим).

Используя неравенство Бесселя (7), ряд Фурье в форме (19) и учитывая полноту ортогональной системы функций, можем получить оценку средней за период мощности периодического колебания f(t):

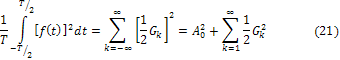
Это равенство Парсеваля показывает, что средняя мощность колебания равна сумме средних мощностей составляющих его ряда Фурье.

Пример 1. Периодическое колебание f(t), показанное на рис.1.а, разложить в ряд Фурье.

Это означает, что необходимо найти коэффициенты ряда, записать ряд и построить спектральную диаграмму.

Сначала заданием f(t)аналитически:

где m - любое целое число..

Полагая m =0 и t₀=0, в соответствии с (20) и (15) найдем коэффициенты ряда

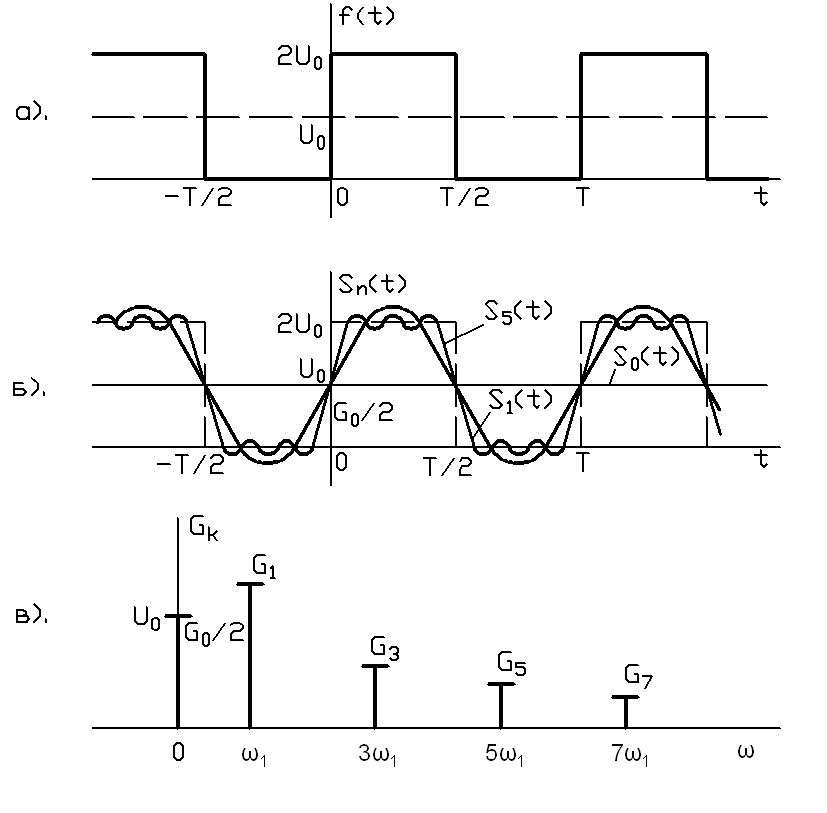Рис.1

Рис.1. Разложение периодической последовательности импульсов в ряд Фурье

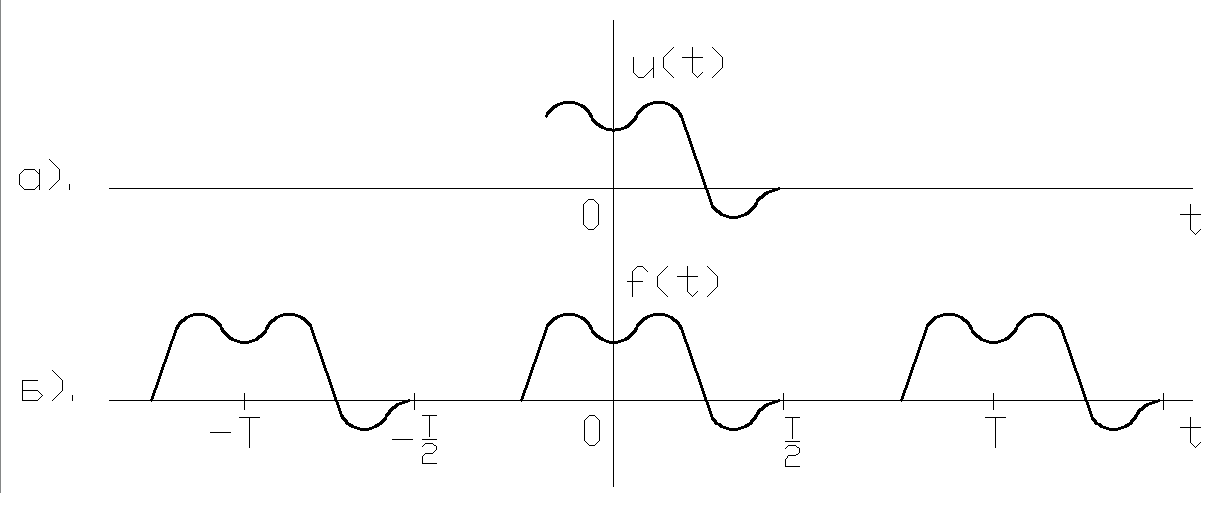Рис.2

Рис.2. Импульс U(t) и периодическая последовательность f(t) таких импульсов

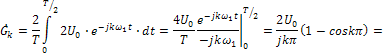
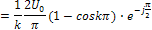
Отсюда при k=0 (после раскрытия неопределенности) - 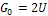, при всех нечетных k (k=1,3,5,...)

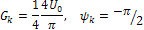
а при четных к (к =2,4,6, ...) - 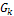=0, т.е. четные гармоники отсутствуют в спектре.

Подставив найденные коэффициенты в выражение (14), получил искомое представление колебания f(t) рядом Фурье:

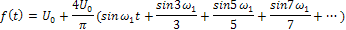
Такой же результат будет, если использовать при решении формулы (12) и (11). На рис.1.б изображены постоянная составляющая и две суммы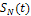

-постоянной составляющей и первой гармоники - ;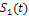

-постоянной составляющей и пяти первых (k=1,3,5)гармоник .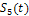

Пунктиром показано заданное колебание f(t). Видим, что с увеличе­нием количества суммируемых гармоник уменьшается погрешность аппро­ксимации.

Спектральная диаграмма приведена на рис.1,в.