Определение декартовой системы координат

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Томский государственный архитектурно-строительный университет»

(ТГАСУ)

Факультет: Инженерно-экологический

Кафедра: Высшая математика

Реферат

На тему: «Поверхности второго порядка».

Выполнил: студент группы 042.4 Розин Николай

Проверила: Сергеева О.А.

Томск 2012

Содержание:

Глава 1:

1. Определение декартовой системы координат 3

2. Подробная характеристика следующих поверхностей:

2.1 Эллипсоид 4

2.2 Однополостный гиперболоид5

2.3 Двуполостный гиперболоид 7

2.4 Эллиптический параболоид 8

2.5 Гиперболический параболоид 10

2.6 Конус второго порядка 12

3. Таблица уравнений поверхностей второго порядка 14

Примечание 18

Список литературы 18

Глава 1.

Определение декартовой системы координат.

Декартова система координат в пространстве, определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат, называется прямоугольной.

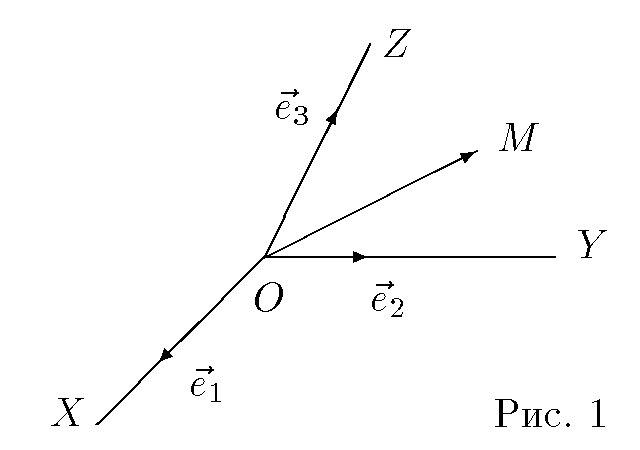
Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты, которых удовлетворяют уравнению вида

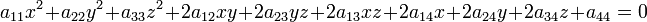
в котором, по крайней мере, один из коэффициентов 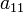, , 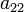, , 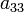, 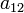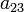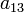отличен от нуля.

Подробная характеристика следующих поверхностей

Эллипсоид

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
:

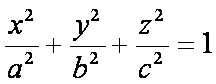
(1)
Уравнение (1) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Оху. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями

(2)

Исследуем уравнения (2) при различных значениях h.

1) Если 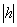> c (c>0), то 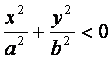и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.

2) Если 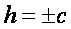, то 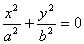и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости 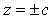касаются эллипсоида).

3) Если 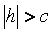, то уравнения (2) можно представить в виде

откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями и 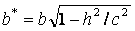. При уменьшении 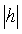значения 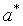и 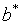увеличиваются и достигают своих наибольших значений при 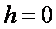, т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосям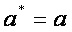и и .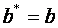

Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.

Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой

Однополосный гиперболоид

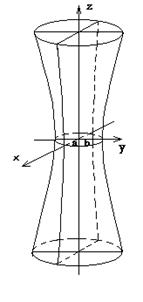
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

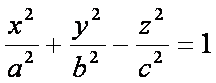(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.

Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy
(
y=0)
и
Oyx (x=0).
Получаем соответственно уравнения

и
из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy
. Линия, получающаяся в сечении, определяется уравнениями

или (4)
из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосям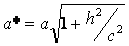и и ,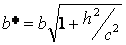

достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a иb*=b. При бесконечном возрастании 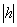величины a* и b* возрастают бесконечно.

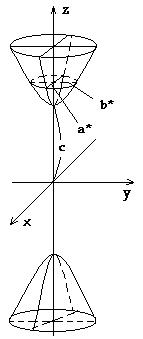
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.

Величины a, b, c называются полуосями однополосного гиперболоида.

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

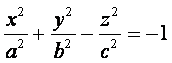(5)

Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.

Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения

и

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями

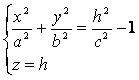или (6)

из которых следует, что при 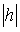>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосям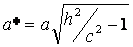и и 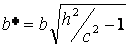. При увеличении 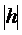величины a* и b* тоже увеличиваются.

При 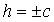уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости 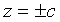касаются данной поверхности).

При 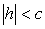уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.

Величина a, b и c называются полуосями двуполостного гиперболоида.

Эллиптический параболоид.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

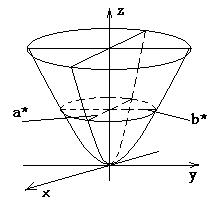
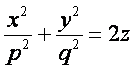(7)

где p>0 и q>0.

Уравнение (7) называется каноническим уравнением эллиптического параболоида.

Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения

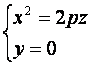и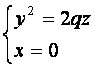

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.

Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями

или (8)

из которых следует, что при 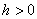плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосям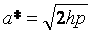и и 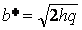. При увеличении h величины aи b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.

Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.

Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.

В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).

Гиперболический параболоид

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением

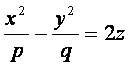(9)

где p>0, q>0.

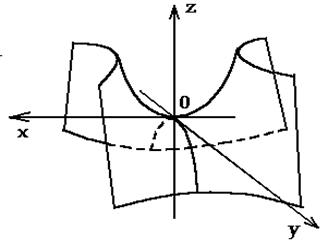
Уравнение (9) называется каноническим уравнением гиперболического параболоида.

Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
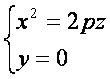(10)

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.

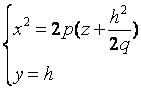
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).

Получаем уравнение

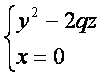
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

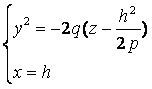
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).

Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения

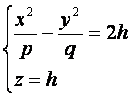или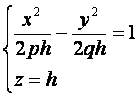

из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых

и

точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.

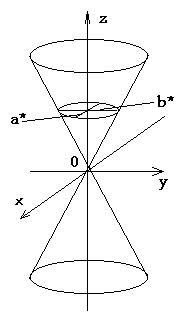
Конус второго порядка

Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

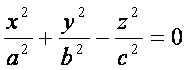(11)

Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Оху (y=0) получаем линию

распадающуюся на две пересекающиеся прямые

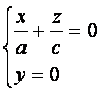и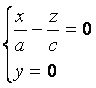

Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые

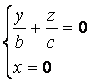и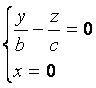

Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Оху. Получим

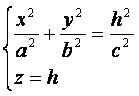или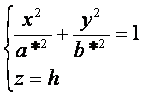

из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями 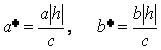. При увеличении абсолютной величины h полуоси a* и b*также увеличиваются.

При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).

Таблица уравнений поверхностей второго порядка

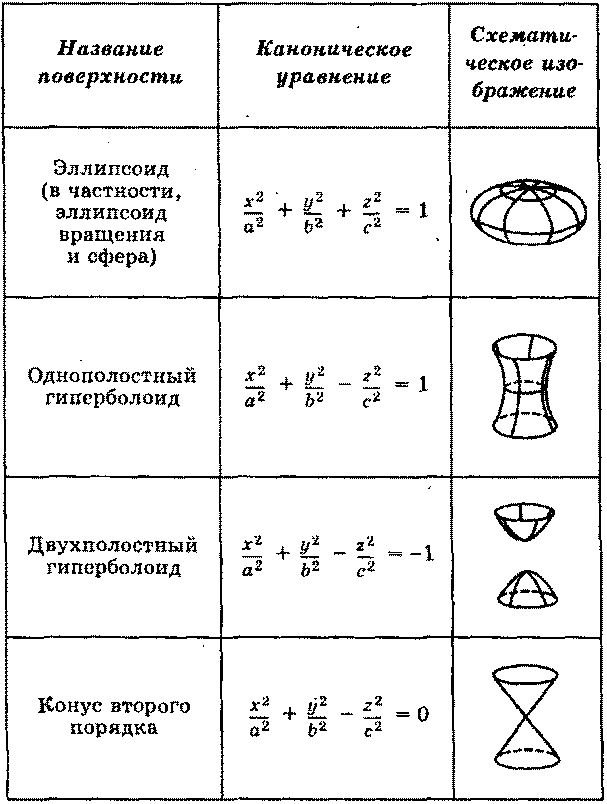
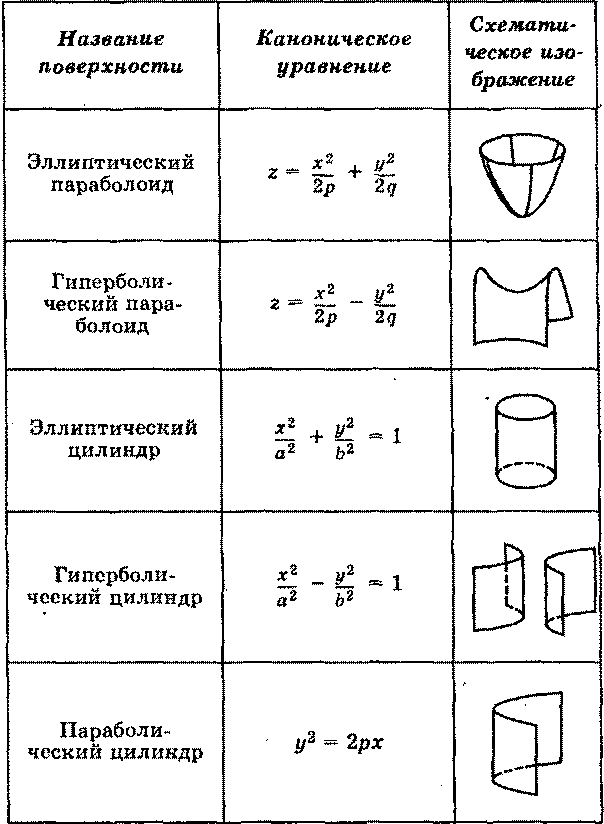
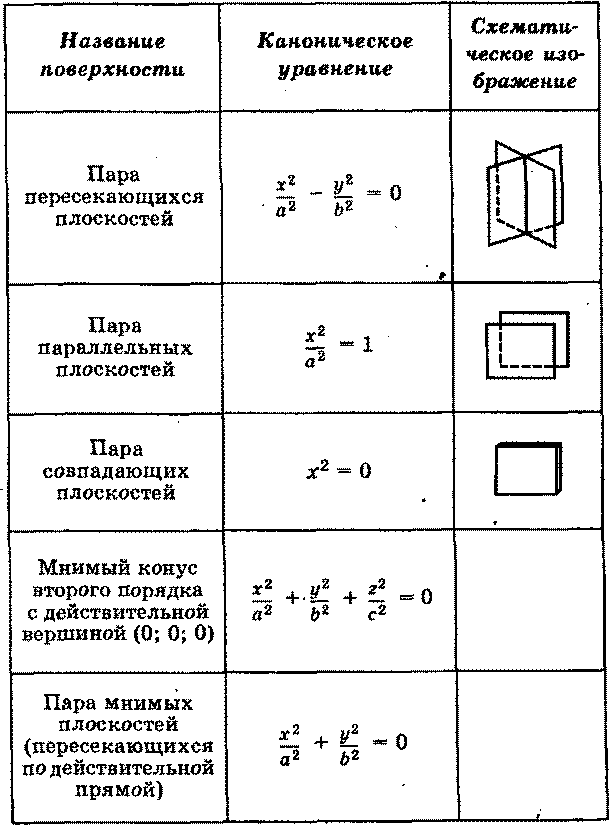
Примечание:

1. Эйлер рассматривал параболический цилиндр как шестой род поверхностей второго порядка; впоследствии эту поверхность, также как цилиндр с эллиптическим и гиперболическим основанием, стали рассматривать как разновидности пяти главных родов.

2. Конус второго порядка мы рассматриваем как частный случай гиперболоидов, подобно тому, как в геометрии на плоскости две пересекающиеся прямые рассматриваются как частная или предельная форма гиперболы. Поэтому конуса в числе главных поверхностей с центром не помещают.

3. Многие свойства гиперболоида, одного из важнейших в теории поверхностей второго порядка, применяется как в начертательной геометрии, так и в искусстве.

Список литературы:

1. Аналитическая геометрия. Курс лекций: С. П. Фиников — Москва, ЛКИ, 2008 г.- 330 с.

2. Аналитическая геометрия: И. И. Привалов — Москва, Лань, 2008 г.- 304 с.

3. Дифференциальная геометрия второго порядка и приложения. Теория Мирона-Атанасиу: Г. Атанасиу, В. Балан, Н. Брынзей, М. Рахула — Санкт-Петербург, Либроком, 2010 г.- 256 с.

4. Задачи и упражнения по аналитической геометрии: О. Н. Цубербиллер — Санкт-Петербург, Лань, 2007 г.- 336 с.

5. Курс аналитической геометрии и линейной алгебры: Д. В. Беклемишев — Москва, ФИЗМАТЛИТ, 2008 г.- 312 с.

6. Локальный электрохимический анализ: В. В. Слепушкин, Ю. В. Рублинецкая — Москва, ФИЗМАТЛИТ, 2010 г.- 312 с.

7. Методы изогеометрической аппроксимации сплайнами: Б. И. Квасов — Москва, ФИЗМАТЛИТ, 2006 г.- 360 с.

8. Минимальные поверхности: — Санкт-Петербург, ФИЗМАТЛИТ, 2003 г.- 352 с

Ссылка 1

http://www.coolreferat.com/%D0%9F%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D0%B8_2-%D0%B3%D0%BE_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%B0

Ссылка 2

http://tvsh2004.narod.ru/gm06.html