Анықталмаған интеграл
Лекция
1. Алғашқы функция және анықталмаған интеграл
Туындының ұғымына келтіретін есептерді қарастырғанда біз дененің 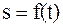 теңдеуімен қозғалу заңы берілгенде осы дененің берілген мезгілдегі жылдамдығы,
теңдеуімен қозғалу заңы берілгенде осы дененің берілген мезгілдегі жылдамдығы,
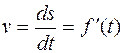
(мұндағы 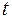 -уақыт,
-уақыт, 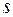 - жүргізілген жол) болатынын көрдік. Яғни берілген мезгілдегі жылдамдықты табу үшін
- жүргізілген жол) болатынын көрдік. Яғни берілген мезгілдегі жылдамдықты табу үшін 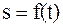 функциясының туындысын тапқанбыз. Бірақ кейде есепті кері шешуге тура келеді: қозғалыстағы дененің берілген мезгілдегі жылдамдығы бойынша, сол дененің қозғалу заңын табу керек. Яғни
функциясының туындысын тапқанбыз. Бірақ кейде есепті кері шешуге тура келеді: қозғалыстағы дененің берілген мезгілдегі жылдамдығы бойынша, сол дененің қозғалу заңын табу керек. Яғни 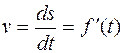 туындысы берілген
туындысы берілген 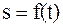 функциясының өзін табу қажет. Бұл есептің дифференциалдық есептеуге кері есеп екенін байқаймыз. Себебі дифференциалдық есептеуде берілген функцияның дифференциалын (туындысын) тапсақ, бұл қарастырылып отырған есепте берілген туындысы бойынша функцияның өзін табу керек.
функциясының өзін табу қажет. Бұл есептің дифференциалдық есептеуге кері есеп екенін байқаймыз. Себебі дифференциалдық есептеуде берілген функцияның дифференциалын (туындысын) тапсақ, бұл қарастырылып отырған есепте берілген туындысы бойынша функцияның өзін табу керек.
Көп жағдайда, әсіресе физика, механика және техника есептерінде туындысы берілген функцияға тең алғашқы (бастапқы) функцияны табу амалдары қарастырылады. Бұл амалды интегралдау деп атайды. Интегралдау амалының дифференциалдау (туындылау) амалына кері амал болатыны айтылды. Сонымен алғашқы функцияның мынадай жалпы анықтамасын беруімізге болады.
Анықтама. Функция 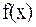 -тің қарастырылып отырған аралықтағы алғашқы (бастапқы) функциясы деп осы аралықтың әр нүктесінде туындысы
-тің қарастырылып отырған аралықтағы алғашқы (бастапқы) функциясы деп осы аралықтың әр нүктесінде туындысы 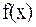 -ке немесе дифференциалы
-ке немесе дифференциалы 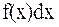 шамасына тең болатын, яғни, аралық нүктелерінде
шамасына тең болатын, яғни, аралық нүктелерінде
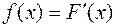 немесе
немесе 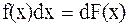
теңдіктерін қанағаттандыратын 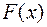 функциясын айтамыз.
функциясын айтамыз.
Мысалға 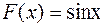 функциясы
функциясы 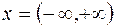 интервалында
интервалында 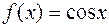 функциясының алғашқы функциясы болып табылады. Шынында да, барлық
функциясының алғашқы функциясы болып табылады. Шынында да, барлық 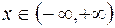 үшін
үшін 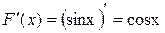 теңдігі орындалады. Бұл функцияның алғашқы функциясы бірмәнді болмайды, өйткені
теңдігі орындалады. Бұл функцияның алғашқы функциясы бірмәнді болмайды, өйткені 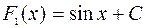 функциясы да С санының кез келген мәндерінде
функциясы да С санының кез келген мәндерінде 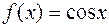 функциясының алғашқы функциясы болады, яғни
функциясының алғашқы функциясы болады, яғни 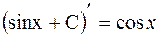 . Осы тұжырым келесі теоремадан шығады:
. Осы тұжырым келесі теоремадан шығады:
Теорема. Егер 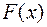 функциясы қарастырылып отырған аралығында
функциясы қарастырылып отырған аралығында 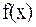 функциясының алғашқы функциясы болса, онда
функциясының алғашқы функциясы болса, онда 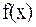 функциясының кез келген басқа алғашқы функциясы
функциясының кез келген басқа алғашқы функциясы 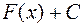 (мұндағы С-кез келген тұрақты сан) түрінде кескінделеді.
(мұндағы С-кез келген тұрақты сан) түрінде кескінделеді.
Дәлелдеу. 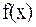 функциясының алғашқы функцияларының бірі
функциясының алғашқы функцияларының бірі 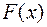 , ал екіншісі
, ал екіншісі 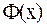 болсын. Сонда анықтама бойынша
болсын. Сонда анықтама бойынша 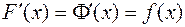 . Сонымен қатар
. Сонымен қатар
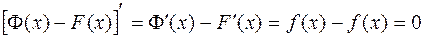 .
.
Осыдан Лагранж теоремасын пайдаланып 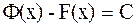 (мұндағы С-ерікті тұрақты) болатынын көреміз. Сонымен
(мұндағы С-ерікті тұрақты) болатынын көреміз. Сонымен 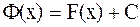 .
.
Бұл теоремаға сүйеніп, берілген функцияның барлық алғашқы функцияларын табу үшін, оның бір алғашқы функциясын тапқаннан кейін оған кезкелген С тұрақты санын қосу жеткілікті деген қорытындыға келеміз.
Қорыта келгенде: 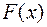 функциясы
функциясы 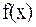 функциясының алғашқы функцияларының бірі болса, онда
функциясының алғашқы функцияларының бірі болса, онда 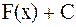 өрнегі, мұндағы С-кез келген тұрақты сан, қарастырылып отырған аралықта
өрнегі, мұндағы С-кез келген тұрақты сан, қарастырылып отырған аралықта 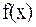 функциясының барлық алғашқы функцияларының жиынтығына тең болады.
функциясының барлық алғашқы функцияларының жиынтығына тең болады.
Енді анықталмаған интеграл ұғымын енгізейік.
Анықтама. 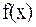 функциясы Х аралығында анықталсын. Осы функцияның Х аралығында барлық алғашқы функцияларының жиынтығын
функциясы Х аралығында анықталсын. Осы функцияның Х аралығында барлық алғашқы функцияларының жиынтығын 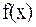 функцияның анықталмаған интегралы деп атайды да оны былай белгілейді:
функцияның анықталмаған интегралы деп атайды да оны былай белгілейді:
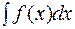 .
.
Демек, анықтама бойынша
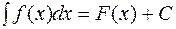 , (1)
, (1)
мұндағы С-кез келген тұрақты сан.
Берілген функцияның анықталмаған интегралын табу амалын функцияны интегралдау деп атайды. Сондықтан туынды үшін кез келген формуланы, яғни 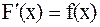 түріндегі формуланы, (1) түрінде жазуға болады. Сонда туындылар кестесін пайдалана отырып кейбір қарапайым функциялардың интегралдарын табамыз. Мысалы,
түріндегі формуланы, (1) түрінде жазуға болады. Сонда туындылар кестесін пайдалана отырып кейбір қарапайым функциялардың интегралдарын табамыз. Мысалы,  теңдеуінен
теңдеуінен 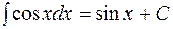 деп жазуға болады.
деп жазуға болады.
2. Анықталмаған интегралдың негізгі қасиеттері.
10. Анықталмаған интегралдың туындысы интеграл астындағы функцияға тең болады, яғни 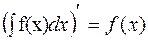 .
.
Дәлелдеуі. Интегралдың анықтамасы бойынша 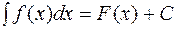 . Осы теңдіктің екі жағынан да туынды алсақ, онда
. Осы теңдіктің екі жағынан да туынды алсақ, онда
 .
.
Келесі қасиеттерді де осылай дәлелдеуге болады.
20. Анықталмаған интегралдың дифференциалы интеграл астындағы өрнекке тең 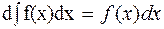 .
.
30. Кез келген 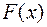 функциясы дифференциалының интегралы сол
функциясы дифференциалының интегралы сол 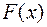 функциясы мен тұрақты С санының қосындысына тең
функциясы мен тұрақты С санының қосындысына тең 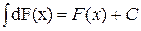 .
.
40. Тұрақты санды интеграл белгісінің алдында шығаруға болады 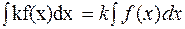 .
.
50. Екі функцияның немесе бірнеше функциялардың қосындысының интегралы қосылғыш функциялар интегралының қосындысына тең
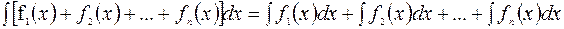 .
.
60. Егер 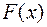 функциясы
функциясы 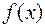 функциясының алғашқы образы болса, онда
функциясының алғашқы образы болса, онда
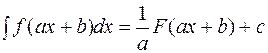 ,
,
мұндағы 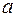 және
және  -тұрақты сандар.
-тұрақты сандар.
3. Негізгі интегралдар кестесі. Анықталмаған интегралдың анықтамасына және туындылау кестесіне сүйеніп, анықталмаған интеграл табудың мынадай кестесін шығару қиын емес:
1. 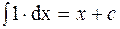 . 2.
. 2. 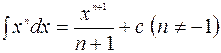 .
.
3. 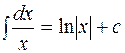 . 4.
. 4. 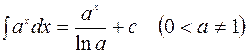 .
.
5. 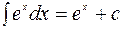 . 6.
. 6. 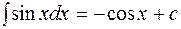 .
.
7.  . 8.
. 8. 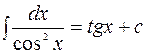 .
.
9. 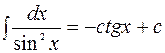 . 10.
. 10. 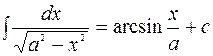 .
.
11.  .
.
12. 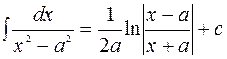 .
.
13. 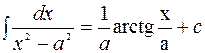 .
.
Кестелік интегралдардың дұрыстығы дифференциалдау амалы арқылы тексеріледі, яғни өрнектің оң жағынан алынған туынды интеграл астындағы функцияға тең болуы керек. Мысалы, 12 формуласын тексерелік:

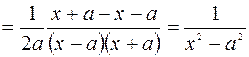 .
.
Басқа формулалар да осылайша тексеріледі. Келтірілген кестені жатқа білу керек.
