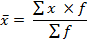Видовые различия средних величин. Взвешенные средние величины.

2 вида: простая и взвешенная

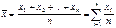
Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней).

Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (f_i), т.е. частота повторения признака.

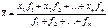
Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса.

В этой формуле числитель дроби выражает прямую зависимость в результате чего, получается реальный экономический смысл. Например, количество рабочих перемноженное на среднемесячную з/п одного рабочего в конечном итоге представляет собой фонд з/п.

Если показатель будет представлен в виде интервала (з/п в 400-500, 500-600, 600-700…), то при расчетах средней необходимо определить середину интервала по средней арифметической простой, а затем производить последующий расчет.

В расчетах средней арифметической взвешенной применяются следующие методы (приемы):

1. Если значение X уменьшить в одно и то же число раз, то занчение средней увеличится в это же число раз.

1. Если значение X увеличить в одно и то же количество раз, то значение средней уменьшится это же количество раз;

2. Если все значения веса f изменить в несколько раз, то значение средней не изменится.

Если для решения задачи используется 3 метода (приема), то эта задача решена способом моментов.

Вторым видом средних величин является средняя гармоническая, которая применяется в двух формах: простой и взвешенной.

Средняя гармоническая применяется в тех случаях, когда известно отдельные значения признака X и объемы признаков.

Объемом может быть: фонд з/п, валовой сбор, сумма товарооборота, стипендиальный фонд, фактический выпуск продукции. В этой формуле наблюдается обратная связь, т.е. при делении 2-ух показателей получается 3 имеющий экономический смысл. Например, при делении фактического товарооборота на количество проданных товаров мы получим цену товара.

Формула средней гармонической простой:

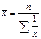
Эта формула обратная средней арифметической простой и предполагается, что сумма объемов в данном случае равна единице.

Средняя гармоническая взвешенная:

;

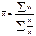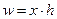
Средняя гармоническая взвешенная равна сумме объемов признаков деленная на сумму отношения объема к признаку.

Средняя квадратическая:

Простая 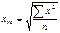Взвешенная х=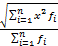

Cредняя геометрическая^

Простая х= 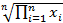Взвешенная x=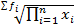

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам т.е. у неё есть частота (вес) признака.