Однородные уравнения первого порядка

№4. Найти общее решение уравнения (х+у)dx–xdy=0.

Решение. Данное уравнение является однородным уравнением первой степени относительно переменных х и у. Действительно,

P(λx, λy)=λx+λy=λ(x+y)= λP(x,y), Q(λx, λy)= –λx=λ(–x)=λQ(x, y).

Положим у=uх, где u – новая функция от х. Найдем дифференциал произведения: dy=хdu+udх. Подставив выражение уи dyв данное уравнение, получим

(х+uх)dх–х(хdu+udх)=0, откуда хdх+uхdх–х²du–хudх=0; хdх–х²du=0 или dх–хdu=0.

Таким образом, получили уравнение с разделяющимися переменными. Разделив переменные и интегрируя, находим

, .

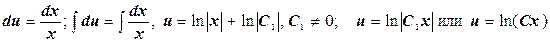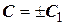Заменяя в полученном выражении u на 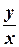, получим у=xln(Cx). Это и есть общее решение данного уравнения.

Отметим, что заданное уравнение можно было сначала привести к виду (9.3.2):

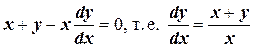. Иначе 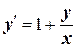. Далее применять указанную выше подстановку и т.д.

№5. Найти общее решение уравнения: .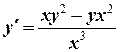

Решение. Это однородное уравнение третьей степени. Преобразуем его к виду (10.6):

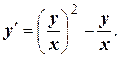
Полагая у=uх, находим 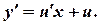Подставим значения 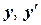в данное уравнение: 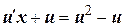. Преобразовывая, получим уравнение с разделяющимися переменными 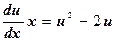. Разделяя переменные и интегрируя, находим:

.

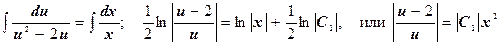Подставим теперь 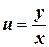в полученное решение. Имеем 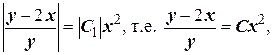где .

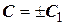Итак, общее решение исходного уравнения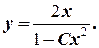

№6. Найти частное решение уравнения 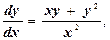если у=–1 при х=1.

Решение. Перепишем уравнение в виде

х²dy = (xy + y²)dx (*)

и воспользуемся подстановкой у=uх. Тогда dy= udх+ хdu. Подставив выражение уи dyв уравнение (*), имеем

х²(udх + хdu)=(х^.uх+u²х²)dх;

x²(udx+xdu)=x²(u+u²)dx;

udx+xdu= udx+ u²dx; т.е.

xdu= u²dx.

Получили уравнение с разделяющимися переменными. Разделив переменные и интегрируя, получим

.

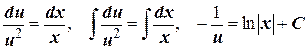Так как u= 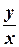, то .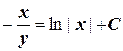

Используя начальные условия х=1, у= –1,имеем1=ln1+C, откуда С=1. Следовательно,

,

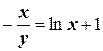Отсюда получаемискомое частное решение данного уравнения .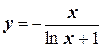

№7. Привести дифференциальное уравнение

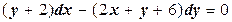к однородному.

Решение. Иначе это уравнение можно записать так 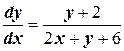. Здесь 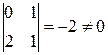, поэтому положив x=u+α, y=v+β, получаем (u+β+2)du–(2u+2α+v+β+6)dv=0, т. е.

(u+(β+2))du–(2u+v+(2α+β+6))dv=0.

Подберем α и βтак, чтобы 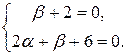Решая систему, находим

α=–2, β=–2. Тогда данное уравнение преобразуется к виду (10.5): 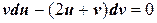, т.е. является однородным.

Линейные уравнения первого порядка

№8. Решить уравнение .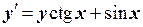

Решение. Здесь P(x)=–ctgx,Q(x)=sinx. Решим уравнение двумя методами.

I. Метод Лагранжа

Найдем сначала общее решение соответствующего ЛОДУ 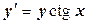, т.е. 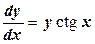. Предположим, что 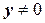(у=0 – решение данного уравнения), разделяя переменные и интегрируя, получим

, ,

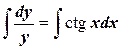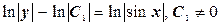Отсюда .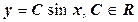

Общее решение ЛНДУ ищем в виде .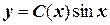

Найдем .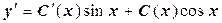

Подставим у и 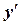в исходное уравнение:

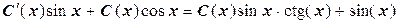или .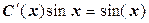

Получ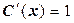или или 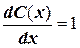. Тогда .

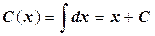Следовательно, общее решение исходного уравнения есть y=(x+C)sin x.

II. Метод Бернулли

Пусть 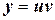. Тогда 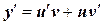и уравнение принимает вид

,

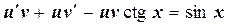или

.

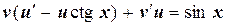Подберем функцию u(x)так, чтобы выражение в скобках равнялось нулю, т.е. решим первое дифференциальное уравнение с разделяющимися переменными ,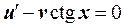

.

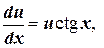
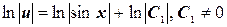Откуда u=С₁×sinx.

Пусть С₁=1, u=sinx.

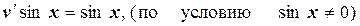, отсюда 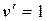, т.е. .

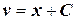Итак, y=(x+C)·sin x, 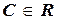есть общее решение данного ЛНДУ.

№9. Найти общее решение уравнения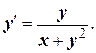

Решение. Данное уравнение не является линейным относительно хи 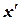. Так как 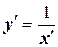, то приведем исходное уравнение к виду (10.6):

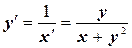, т.е. 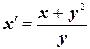или 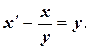Далее это ДУ решим двумя методами: