Введение. Рекомендовано редакционно-издательским советом университета

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ 8, 28, 29, 30, 129, 130

МОСКВА - 2008

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

ФИЗИКА

Рекомендовано редакционно-издательским советом университета

в качестве методических указаний для студентов институтов

ИУИТ, ИСУТЭ, ИЭФ, ИТТОП, ИКБ, вечернего факультета

Под редакцией Е.А.Серова

МОСКВА -2008

УДК 53

М-54

Ильин С.И., Лямзова И.А., Прунцев А.П., Селезнёв В.А. Физика. Методические указания к лабораторным работам 8, 28, 29, 30, 129, 130 // Под ред. Е.А.Серова. – М.: МИИТ, 2008. – 66 с.

Методические указания содержат описания лабораторных работ по общему курсу физики, предназначенных для студентов первого и второго курсов институтов ИУИТ. ИСУТЭ, ИТТОП, ИЭФ, ИКБ, вечернего факультета.

С.И. Ильин (работа 28), И.А. Лямзова (работа 8), А.П. Прунцев (работы 30, 130), В.А. Селезнёв (работа 129). Работа 29 переработана В.А. Селезнёвым.

© Московский государственный

университет путей сообщения

(МИИТ), 2008

Работа 8

ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ

СВЯЗАННОЙ СИСТЕМЫ ТЕЛ

Цель работы: Определение периода колебаний и коэффициента затухания системы, содержащей груз, блок и пружину.

Приборы и принадлежности: стойка с блоком и пружиной, набор грузов с подставкой, секундомер.

Введение

Колебаниями называются процессы, при которых какая-либо физическая величина принимает многократно, через равные (или почти равные) последовательные промежутки времени, одни и те же значения.

Природа этой физической величины может быть самой различной. Например, это может быть отклонение шарика, подвешенного на нити, от положения равновесия, или угол, который составляет эта нить с вертикалью, или сила тока в электрическом колебательном контуре, изменяющаяся относительно среднего значения.

Несмотря на различную природу, колебания самых разнообразных физических величин имеют много общего. Все они характеризуются периодом - промежутком времени, через который значения колеблющейся величины начинают повторяться, амплитудой – наибольшим отклонением от среднего значения. Часто при колебаниях изменение с течением времени различных по природе физических величин носит одинаковый характер, т.е. эти величины изменяются по одному и тому же закону с течением времени. В этом случае колебания описываются одинаковыми математическими уравнениями.

Общие для всех колебаний закономерности можно изучать на примере какой-либо одной физической величины. Здесь мы будем рассматривать механические колебания.

Механическими колебаниями называются такие колебания, для которых изменяющейся физической величиной является отклонение материальной точки (или системы материальных точек) от положения равновесия (а также ее скорость, ускорение и т. д.).

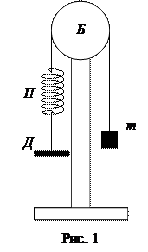Рассмотрим систему, состоящую из пружины П, блока Б и груза m. Ее схематическое изображение дано на рис.1. Один конец пружины прикреплен к держателю Д, другой – к нерастяжимой нити, перекинутой через блок и соединенной с грузом m. Нить при движении не проскальзывает относительно блока. Блок представляет собой однородный диск, укрепленный на неподвижной оси.

При отклонении груза от положения равновесия растяжение пружины приводит к возникновению упругой силы, возвращающей систему в положение равновесия. Если груз отклонить и отпустить, система начнет совершать колебания с периодом Т. Такие колебания называются свободными. Действие сил трения в системе приведет к тому, что колебания будут затухающими, т.к. механическая энергия будет переходить в тепло.

Найдем выражение для периода колебаний системы. Для этого рассмотрим силы, действующие на каждое из тел системы, и составим дифференциальное уравнение колебаний. Вывод проделаем, предполагая, что силы трения малы, и ими можно пренебречь. Массы пружины и нити примем равными нулю, так как они значительно меньше масс груза и блока. При рассмотрении сил и перемещения тел системы будем считать положительным направлением такое, при котором блок вращается по часовой стрелке (см. рис. 1).

На груз действует сила тяжести и сила F₁, равная силе натяжения нити, к которой привязан груз, направленные в противоположные стороны.

По второму закону Ньютона

ma = mg – F₁, (1)

где а – ускорение груза.

Угловое ускорение блока создается разностью сил натяжения нити с двух его сторон. Применив основной закон динамики вращательного движения, напишем для блока

Je= (F₁– F₂)r , (2)

где J – момент инерции блока; e – его угловое ускорение; r – радиус блока; F₂ – натяжение отрезка нити, привязанного к пружине.

Так как блок является однородным диском, то его момент инерции и масса m₀ связаны соотношением

J = ½ m₀r². (3)

Рассмотрим силы, действующие на отрезок нити, соединенный с пружиной. Кроме силы натяжения на него действует сила упругости пружины. В соответствии с законом Гука абсолютное значение этой силы связано с удлинением пружины x соотношением.

F_УПР= – kx, (4)

где k – коэффициент жесткости пружины.

Т.к. масса нити равна нулю, то по второму закону Ньютона

F₂– F_УПР = 0. (5)

Движение системы будем описывать с помощью переменной y, обозначающей смещение груза от положения равновесия. Так как в положении равновесия пружина уже находится в растянутом состоянии, то ее удлинение x не равно смещению груза y. Они связаны соотношением

x = y + mg/k. (6)

Линейное ускорение груза равно второй производной по времени от смещения: a = 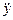. Угловое ускорение блока связано с его тангенциальным ускорением, равным ускорению груза соотношением

e= a/r = 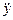/r. (7)

Уравнения (1), (2) и (5) сведем в систему, использовав соотношения (3), (4), (6) и (7):

m 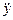= mg – F₁,

½ m₀ 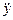= F₁– F₂, (8)

ky + mg = F₂.

Подставив выражения для F₁ и F₂ из первого и третьего уравнений системы во второе, получим

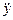+ [k/(m + ½ m₀)]y = 0. (9)

Обозначим [k/(m + ½ m₀)] = w₀², тогда выражение (9) примет вид

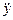+ w₀² y = 0. (10)

Решением уравнения (10) является функция

y = Asin(w₀t + a) или y = Acos(w₀t + a¢), (11)

где А – амплитуда колебаний; (w₀t + a) – фаза колебаний; w₀ – циклическая частота.

Гармоническими называются колебания, при которых изменение физической величины, например смещения груза у, с течением времени (закон колебаний) выражается формулой (11).

Так как движение рассматриваемой системы (рис. 1) при отсутствии сил трения описывается уравнениями (9) – (11), то система колеблется по гармоническому закону с периодом

T₀ = 2p/w₀. (12)

При отсутствии трения величина А – постоянная во времени, колебания называются свободными незатухающими, а уравнения (9) и (10) – дифференциальными уравнениями свободных незатухающих колебаний.

Учет силы трения, всегда действующей в реальных механических системах, приводит к изменению уравнения (10). В нем появляется еще один член, и оно приобретает вид

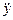+ 2b 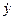+ w₀²y = 0, (13)

где b - коэффициент затухания. Решение уравнения (13) имеет вид

y = A₀e^-bt sin(w₀t + a) или y = A₀e^-bt cos(w₀t + a¢), (14)

где A₀ – постоянная; A₀ e^-bt – убывающая амплитуда колебаний.

Таким образом любое механическое колебание происходит с затратами энергии на работу против сил трения. При этом амплитуда колебательного движения А с течением времени убывает, происходит затухание колебаний (рис. 2.)

Графически изменение амплитуды по времени изображается огибающей кривой затухающих колебаний (пунктирная линия на рис. 2).

Частота затухающих колебаний w отличается от частоты w₀ незатухающих колебаний и равна

w = 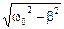. (15)

Из этого следует, что период затухающих колебаний T = 2p/w больше периода незатухающих колебаний T₀ = 2p/w₀.