ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ. Цель работы: изучить зависимость амплитуды колебаний упругой пластинки от частоты внешней силы, определить коэффициент затухания и добротность.

Цель работы: изучить зависимость амплитуды колебаний упругой пластинки от частоты внешней силы, определить коэффициент затухания и добротность.

Оборудование: упругая пластинка, электромагниты, звуковой генератор ADG-1005, осциллограф ADS-2111M.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Собственные колебания маятников всегда являются затухающими, так как кроме возвращающей упругой силы F_упр = −kx еще действуют силы сопротивления 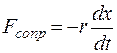. Здесь 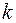и r – коэффициенты упругости и сопротивления. Чтобы колебания были незатухающими, необходимо приложить к маятнику еще внешнюю периодическую силу 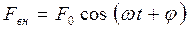. Маятник начнет совершать вынужденные колебания с частотой внешней силы, Исследуем вынужденные.колебания маятника, решив уравнение второго закона Ньютона

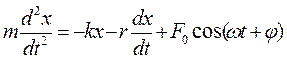. (1)

Разделив на массу, приведем дифференциальное уравнение к канонической форме

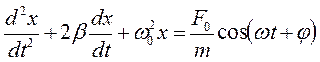. (2)

Здесь введены обозначения: 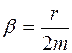– коэффициент затухания, 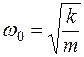– циклическая частота собственных свободных колебаний.

Как показывает опыт, если на маятник начать действовать периодической силой, то вынужденные колебания устанавливаются не сразу. В течение некоторого времени на вынужденные колебания накладываются собственные колебания. Но так как собственные колебания являются затухающими, то со временем они исчезают и маятник совершает только вынужденные колебания. Их частота равна частоте внешней периодической силы. Поэтому частное решение уравнения (2) будем искать для установившихся вынужденных колебаний в виде

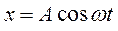, (3)

где 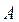– амплитуда колебаний, то есть наибольшее смещение от положения равновесия. Чтобы убедиться, что функция (3) является решением, следует подставить ее, первую и вторую производные в уравнение (2):

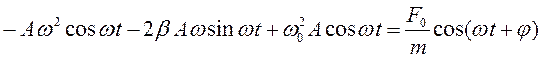. (4)

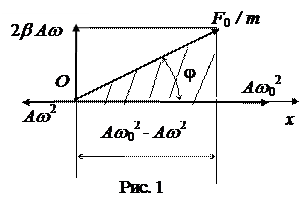Это уравнение содержит две неизвестные величины: амплитуду колебаний А и сдвиг фаз между силой и смещением 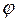. Для их определения воспользуемся заменой тригонометрического уравнения геометрическим представлением в виде векторной диаграммы (рис. 1). Для этого из полюса О следует провести векторы, длины которых равны амплитудам, а угол относительно полярной оси равен начальным фазам. Теперь, если вращать векторы вокруг полюса О против часовой стрелки с угловой скоростью, равной частоте ω, то их проекции будут равны членами уравнения (4). На векторной диаграмме сумма векторов амплитуд левой части уравнения должна быть равна вектору амплитуды правой части уравнения (4). Поэтому запишем теорему Пифагора для заштрихованного треугольника

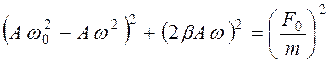. (5)

Отсюда

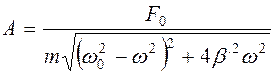. (6)

Амплитуда сначала с ростом частоты возрастает от величины статического смещения 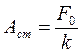, достигает наибольшего значения и затем снова уменьшается (рис. 2). Сильное увеличение амплитуды вынужденных колебаний при некоторой частоте называется резонансом. Чтобы получить условие резонанса, следует приравнять производную от подкоренного выражения (6) к нулю. Откуда получим 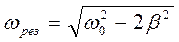. Резонанс наступает при частоте вынуждающей силы, близкой к частоте свободных колебаний. Подставив частоту резонансав (6), получим

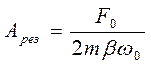. (7)

Резонанс обусловлен тем, что направление скорости тела и направление силы совпадают в течение всего периода колебания. Поэтому отбор мощности от источника оказывается наибольшим (N = F∙V). Чем меньше сопротивление среды (β→0), тем выше и острее резонанс. По резонансной кривой можно определить коэффициент затухания. Проведем на уровне 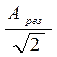горизонтальную линию (рис. 2). Абсциссы точек пересечения определим, подставив в левую часть уравнения (6) амплитуду при резонансе (7), деленную на 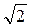. Решив квадратное уравнение относительно корней ω₁ и ω₂, получим, что коэффициенту затухания равен полуширине резонансной кривой: .

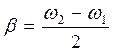Другим параметром, характеризующим резонансные свойства колебательной системы, является добротность, равная отношению энергии колебаний к потерям энергии за период 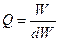Добротность также равна отношению амплитуды резонанса (7) к статическому смещению: .

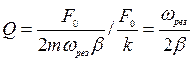Установка для исследования вынужденных колебаний представляет собой упругую пластинку с приклеенными постоянными магнитами. Вынужденные колебания создаются действием на магнит переменного магнитного поля катушки, которая подключена к звуковому генератору. Амплитуду определяют по ЭДС приемной катушки.

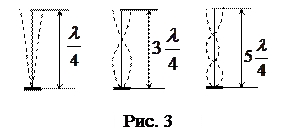В пластинке, в отличие от маятника, масса распределена по всей длине. Поэтому, если колебания возникнут у основания, то по пластинке будет распространяться упругая волна. Достигнув свободного конца, она отразится и сложится с бегущей волной. Резонанс наступит, если в пластинке вследствие интерференции волн возникнет стоячая волна. При этом в месте закрепления пластинки должен быть узел, а на свободном конце – пучность колебаний. Пластинка может иметь набор резонансных частот, (рис. 3).

ВЫПОЛНЕНИЕ РАБОТЫ

1. Включить генератор в сеть 220 В. На панели генератора нажать, если не светится, кнопку частоты Freq и установить частоту около 20 Гц по левому индикатору дисплея. Нажать кнопку Ampl, установить напряжение выхода 20 В по правому индикатору. Установки производятся поворотом ручки регулятора или набором цифр на клавиатуре. Изменяемый разряд числа на дисплее выбирается двумя кнопками под регулятором.

2. Изменяя частоту генератора регулятором через 1 Гц в интервале от 20 до 100 Гц, наблюдать за колебаниями пластинки. Зафиксировать три формы колебания, рис. (3) на трех частотах резонанса. Зарисовать в отчете формы колебаний пластинки с указанием частот.

2. Включить осциллограф в сеть 220 В. Установить на генераторе частоту самого сильного резонанса. Поворотом ручек усилителя Volts/div канала CH-2 и горизонтальной развертки Sek/div отрегулировать изображение на дисплее.

3. Изменяя частоту через 0,1 Гц в области резонанса измерить максимальную амплитуду сигнала. Измерения производятся либо по шкале дисплея в миллиметрах, либо в единицах напряжения с помощью курсора. Для этого нажать на панели кнопку Kursor и совмещать верхнюю и нижнюю линии курсора с краями осциллограммы поворотом ручек смещения обоих каналов Vertikal position. В окне диалога в левом углу дисплея считать напряжение Δy=А. Результаты записать в середину таблицы. Повторить измерения в диапазоне более высоких и более низких частот в интервале ±2 Гц с более редким интервалом. Выключить приборы.

Частота ν, Гц

Амплитуда А, В

4. Построить график зависимости амплитуды колебаний от частоты А(ν) размером не менее полстраницы. Около точек провести плавную кривую линию.

5. Определить коэффициент затухания Для этого на графике 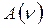провести горизонтальную линию с ординатой 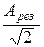. Определить частоты точек пересечения с линией ν₁ и ν₂ (рис. 2). Среднее значение коэффициент затухания (при Δω =2πΔν) равно <β>=πΔν.

6. Определить добротность колебательной системы .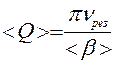

7. Оценить систематическую погрешность измерения добротности 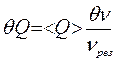, при θν = 0,1 Гц.

8. Записать результат измерений Q=<Q>±θQ, Р = 0,90. Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Запишите уравнение второго закона Ньютона для вынужденных колебаний маятника. Назовите силы, действующие на маятник.

2. Получите на основании второго закона Ньютона дифференциальное уравнение вынужденных колебаний.

3. Выведите формулу для амплитуды вынужденных колебаний с помощью векторной диаграммы.

4. Изобразите график зависимости амплитуды от частоты силы. Дайте определение резонанса. В чем причина резонанса?

5. Объясните, как можно определить коэффициент затухания маятника по резонансной кривой.

6. Объясните, почему пластинка обладает набором резонансных частот? Каким формам колебаний они соответствуют? Сколько длин волн укладывается на пластинке в каждом случае?

Работа 12