Определение логарифмического декремента
Исследование законов поступательного движения
И проверка основного закона динамики
Литература
1. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. §§ 1.1 – 1.4; 2.1 – 2.5
Введение
Поступательным движением твердого тела называется такое движение, при котором любая прямая линия, проведенная в теле и неизменно связанная с ним, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки твердого тела обладают одинаковыми скоростями и ускорениями. Поэтому изучение поступательного движения твердого тела сводится к изучению движения любой точки тела.
Скоростью движения материальной точки называется величина равная первой производной от радиуса-вектора 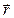 , определяющего положение точки в пространстве по времени t
, определяющего положение точки в пространстве по времени t
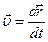 (1)
(1)
Вектор скорости материальной точки в данный момент времени направлен по касательной к траектории в данной точке. Модуль скорости (ее численное значение) определяется соотношением:
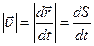 , (2)
, (2)
где dS – элементарная длина траектории (элементарный путь).
Ускорением 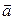 материальной точки называется величина, равная первой производной от вектора скорости
материальной точки называется величина, равная первой производной от вектора скорости 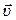 по времени t
по времени t
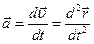 (3)
(3)
Направление вектора 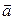 совпадает с направлением вектора приращения скорости
совпадает с направлением вектора приращения скорости 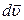 .
.
При равномерном прямолинейном движении 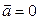 , следовательно,
, следовательно, 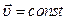 и
и 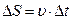 (4)
(4)
При равнопеременном прямолинейном движении материальной точки вдоль какой-либо прямой 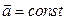 . Скорость материальной точки (или тела) в любой момент времени определяется соотношением
. Скорость материальной точки (или тела) в любой момент времени определяется соотношением
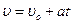 , (5)
, (5)
где 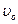 – скорость точки в начальный момент времени при
– скорость точки в начальный момент времени при 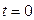 .
.
Путь, как функция времени, при равнопеременном прямолинейном движении вычисляется по формуле
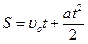 (6)
(6)
В основе классической динамики лежат три закона Ньютона.
1 закон Ньютона. Всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния (закон инерции).
Суть закона заключается в существовании инерциальных систем отсчета, для которых выполняется первый закон Ньютона.
2 закон Ньютона – основной закон динамики поступательного движения. Скорость изменения импульса материальной точки равна действующей на нее силе, и изменение импульса происходит в направлении действия силы.
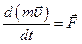 (7)
(7)
Отсюда следует, что
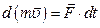 (8)
(8)
т.е. элементарное изменение импульса материальной точки равно импульсу действующей на нее силы и происходит по направлению той прямой, по которой эта сила действует. В такой формулировке второй закон Ньютона применим и в механике для тел с переменной массой.
При постоянной массе тела 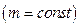 второй закон можно записать в следующем виде:
второй закон можно записать в следующем виде:
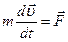 или
или 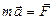 (9)
(9)
В основном законе динамики поступательного движения 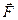 – равнодействующая всех сил, действующих на тело.
– равнодействующая всех сил, действующих на тело.
3 закон Ньютона. Силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению
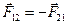 (10)
(10)
При этом силы действия и противодействия имеют одинаковую природу, но приложены к разным телам.
Описание прибора и метода измерения
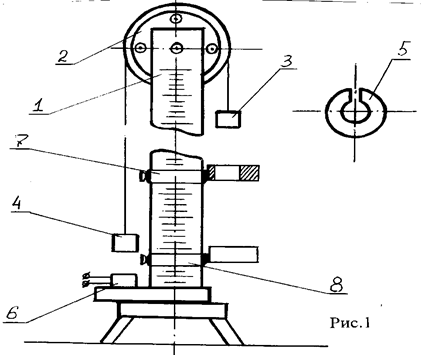 |
Общая схема лабораторной установки представлена на рис. 1.
Рейка 1 со шкалой установлена вертикально. На верхнем конце рейки имеется легкий алюминиевый блок 2, вращающийся с незначительным трением. Через блок перекинута нить, на концах которой подвешены два груза 3 и 4 одинаковой массой М. Груз 4 может удерживаться в нижнем положении электромагнитом 6.
Масса грузов 3 и 4 может быть увеличена за счет небольших добавочных грузов (перегрузков) 5. Если на груз 3 положить один из перегрузков 5 массой m, то вся система начинает двигаться равноускоренно. В комплект добавочных грузов входят несколько перегрузков, что позволяет исследовать движение с различными ускорениями.
Платформы 7 и 8 с помощью винтов могут быть укреплены в любом месте рейки 1. Сплошная платформа 8 служит для остановки груза 3, кольцевая платформа 7 – для снятия перегрузка 5 с груза 3 во время движения. Движение груза 3 от его верхнего положения до кольцевой платформы 7 происходит равноускоренно под действием перегрузков. После снятия перегрузков движение груза 3 между платформами 7 и 8 становится равномерным и происходит с постоянной скоростью, равной скорости, которую имел груз 3 в момент снятия перегрузков, т.е. в конце равноускоренного движения.
Время t, в течение которого происходит равноускоренное движение измеряется одним секундомером; а время t / , в течение которого происходит равномерное движение – другим секундомером. Секундомеры включаются и выключаются автоматически: при отключении электромагнита 6 – включается первый секундомер, при снятии перегрузков – первый секундомер отключается, второй – включается; отключение второго секундомера происходит, когда груз 3 касается платформы 6.
Целью первой части работы является проверка формул пути и скорости равноускоренного движения (см. формулы 5 и 6). Если начальная скорость тела равна нулю, то
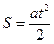 (11)
(11)
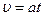 (12)
(12)
Из выражения (11) видно, что если ускорение тела постоянно, то путь S, пройденный телом за время t, должен быть пропорционален квадрату времени t2, т.е.
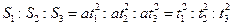 (13)
(13)
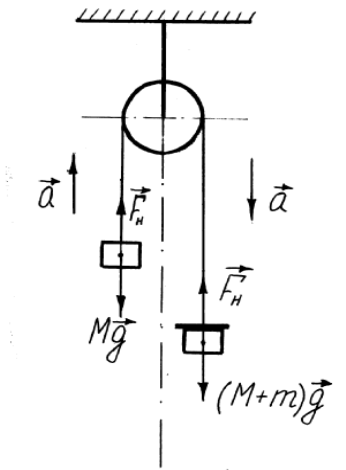 |
Для проверки этого соотношения проводят несколько измерений времени прохождения грузов 3 различных путей S (меняется каждый раз расстояние от исходного положения груза 3 до кольцевой платформы). Если на груз 3 положить добавочный груз 5 массой m, то на каждый груз 3 и 4 будут действовать две силы – сила тяжести и сила натяжения нити, под действием которых грузы начнут двигаться. Предполагая, что нить и блок не имеют массы, нить нерастяжима, а сила трения очень мала, получим, что ускорение правого и левого грузов будут одинаковы по величине и противоположны по направлению, а сила натяжения нити одинаковы справа и слева (рис. 2)
Рис. 2
На основании второго закона Ньютона можно написать для:
груза 3 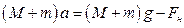 (14)
(14)
груза 4 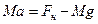 (15)
(15)
Находя из этих уравнений ускорение а , получим
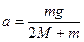 (16)
(16)
Из соотношения (16) видно, что ускорение системы грузов зависит от массы перегрузков. Следовательно, для того, чтобы в различных опытах грузы двигались с одинаковыми ускорениями, масса перегрузков должна быть одинакова.
Измерив, время t прохождения грузами различных путейS, проверяют соотношение (13), а, следовательно, и формулу (11).
Выражение (12) показывает, что скорость тела при постоянном ускорении пропорциональна времени его движения. Следовательно, можно записать
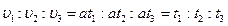 (17)
(17)
При проверке этого соотношения используются замеры времени t прохождения грузом 3 путей S в предыдущем опыте. Соответствующие значения скоростей определяются следующим образом. При прохождении грузом 3 кольцевой платформы добавочный груз снимается и, начиная с этого момента времени, вся система движется по инерции равномерно с той скоростью, которую она приобрела в момент снятия перегрузка, т.е. в конце равноускоренного движения. Чтобы определить эту скорость, необходимо замерить время t/ прохождения грузом 3 пути 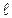 между платформами 7 и 8. Тогда
между платформами 7 и 8. Тогда
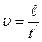 (18)
(18)
Подставляя значения u и t в (17), проверяют правильность формулы (12).
Вторая часть работы состоит в проверке основного закона динамики поступательного движения, который при постоянной массе и силе имеет вид:
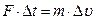 (19)
(19)
Если начальная скорость тела равна нулю, то
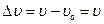 (20)
(20)
т.е. изменение скорости за время 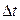 численно равно скорости тела в момент времени t.
численно равно скорости тела в момент времени t.
Если в различных опытах масса системы тел одинакова, а сила различна, то, учитывая (19), можно записать
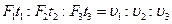 (21)
(21)
Для того, чтобы менять силу, не изменяя массы системы, в каждом опыте используются все добавочные грузы. Перегрузки кладутся и на опускающийся груз 3, и на поднимающийся груз 4 в различных сочетаниях. При этом сила будет определяться разностью масс добавочных грузов на опускающемся и на поднимающемся грузе, а масса движущейся системы будет равна сумме масс основных и всех добавочных грузов.
При проведении этих опытов кольцевая платформа устанавливается вплотную к сплошной. Поэтому груз 3 движется равноускоренно от верхнего положения до сплошной платформы, проходя при этом путь h. Измерив время этого движения t и зная путь h можно вычислить конечную скорость равноускоренного движения по формуле:
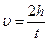 (22)
(22)
Подставляя значение F , t и u в соотношение (21), проверяют основной закон динамики поступательного движения.
Проверка второго закона Ньютона носит приближенный характер, т.к. в расчетах мы пренебрегаем силой трения, массами блока и нити.
Порядок выполнения работы
1. Проверка формул пути и скорости равноускоренного движения
1. Отмечают начальное (верхнее) положение груза 3.
2. Измеряют длину груза 3.
3. Устанавливают кольцевую и сплошную платформы так, чтобы пути S и 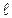 соответствовали заданным величинам. При этом следует учитывать длину груза 3 и его начальное положение.
соответствовали заданным величинам. При этом следует учитывать длину груза 3 и его начальное положение.
4. Грузы 3 и 4 устанавливают в начальное положение. При этом груз 4 должен удерживаться электромагнитом 6.
5. На груз 3 кладут перегрузки 5 (их количество задается преподавателем).
6. Выключают электромагнит, при этом вся система грузов приходит в движение, а секундомеры отмечают время t и t/ так, как описано выше.
7. Показания секундомеров t и t/ записывают в таблицу 1. Опыт повторяется три раза.
8. Повторяют опыт при других расположениях платформ.
9. Результаты измерений записывают в табл. 1.
2. Проверка основного закона динамики.
1. Устанавливают кольцевую платформу на заданное расстояние h. Сплошную платформу закрепляют вплотную под кольцевой.
2. Устанавливают грузы 3 и 4 в начальное положение.
3. На грузы 3 и 4 добавляют перегрузки 5 определенной массы.
4. Выключают электромагнит, и после остановки системы грузов, отсчитывают время t прохождения грузом 3 пути h по показаниям секундомера. Результаты измерений записывают в таблицу 2. Опыт повторяют три раза.
5. Производят аналогичные измерения с помощью различных сочетаний перегрузков, не изменяя их общей массы. Высоту во всех опытах оставляют постоянной. Результаты измерений записывают в табл. 2.
Обработка результатов измерений
1. Проверка формул пути и скорости равноускоренного движения
1. Записываются исходные данные:
масса грузов 3 и 4 M =
масса добавочных грузов m =
начальная скорость 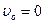
1. Результаты измерений записываются в табл. 1
Таблица 1
| № п/п | Проверка формул пути | Проверка формул скорости | Ускорение | |||||||
| S, м | t, с | tср, с | 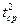 , с2 , с2 | 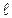 , м , м | t/ , с | 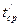 , с , с | 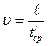 , м/с , м/с | 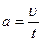 , м/с2 , м/с2 | 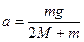 , м/с2 , м/с2 | |
3. Вычисляют средние значения промежутков времени tср и 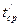 для каждого значения S и
для каждого значения S и 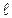 .
.
4. Вычисляют значения скоростей по формуле (18).
5. Вычисляют значения ускорений по формулам (12) и (16) и сравнивают их между собой.
6. По результатам трех опытов значения S и t2 сравниваются между собой согласно формуле (13) и делается вывод о справедливости формулы пути равноускоренного движения.
7. Аналогично предыдущему пункту сравниваются между собой значения u и t,согласно формуле (17), делается вывод о справедливости формулы скорости равноускоренного движения.
2. Проверка основного закона динамики поступательного движения
1. Записываются исходные данные:
высота поднятия груза h =
2. Результаты измерений записываются в табл. 2.
Таблица 2
 Величина № опыта Величина № опыта | F, Н | t, с | tср, с | 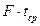 , Н × с , Н × с | 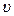 , м/с , м/с |
3. Для каждого опыта вычисляется среднее значение времени tср.
4. Вычисляются значения 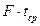 и скорости
и скорости 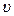 по формуле (22) для каждого опыта и полученные результаты также заносятся в табл. 2.
по формуле (22) для каждого опыта и полученные результаты также заносятся в табл. 2.
5. Вычисленные значения 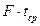 и
и 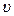 сравниваются между собой, согласно формуле (21), и делается вывод о справедливости основного закона динамики поступательного движения.
сравниваются между собой, согласно формуле (21), и делается вывод о справедливости основного закона динамики поступательного движения.
Контрольные вопросы
1. Что такое скорость? Как направлен вектор мгновенной линейной скорости?
2. Что называется ускорением?
3. Как связаны между собой скорость и пройденный путь при равномерном прямолинейном движении?
4. Что называется импульсом тела? Как направлен вектор импульса тела?
5. Сформулируйте законы динамики поступательного движения.
6. Чему равна скорость изменения импульса тела, если на тело действует постоянная сила?
7. Дайте описание лабораторной установки.
8. В чем состоит метод проверки формулы пути и скорости равноускоренного движения?
9. Как проверяется основной закон динамики.
Лабораторная работа 10
Определение логарифмического декремента
