Входные и взаимные проводимости ветвей
Используя принцип наложения, можно записать уравнение, для нахождения тока в произвольной ветви линейной электрической цепи, например в ветви 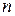 , в виде
, в виде
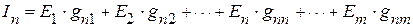 .
.
В приведенном уравнении, ток 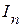 обозначает ток в ветви
обозначает ток в ветви 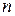 , а
, а 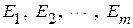 - ЭДС соответветсвенно в первой, второй и
- ЭДС соответветсвенно в первой, второй и 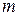 – ой ветвях.
– ой ветвях.
Каждый из множителей, в приведенном уравнении, с двумя одинаковыми индексами 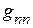 называют входной проводимостью ветви
называют входной проводимостью ветви 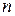 , а с двумя различными индексами
, а с двумя различными индексами 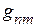 называют взаимной проводимостью ветвей
называют взаимной проводимостью ветвей 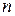 и
и 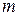 .
.
Численные значения входных и взаимных проводимостей ветвей определяются следующим путем. Приравниваем в произвольной рассматриваемой схеме все источники напряжения к нулю, кроме 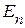 . Тогда, из приведенного уравнения, для нахождения тока в произвольной ветви электрической цепи, ток в
. Тогда, из приведенного уравнения, для нахождения тока в произвольной ветви электрической цепи, ток в 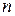 – ой равен
– ой равен
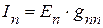 .
.
Откуда 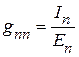 .
.
Следовательно, входная проводимость произвольной ветви электрической схемы, определяется отношением величины тока 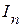 к ЭДС источника напряжения
к ЭДС источника напряжения 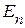 в этой при равных нулю ЭДС источников напряжения в остальных ветвях схемы.
в этой при равных нулю ЭДС источников напряжения в остальных ветвях схемы.
Источник напряжение с ЭДС 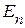 , включенный в ветвь
, включенный в ветвь 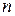 , вызывает токи во всех ветвях произвольной линейной электрической цепи. Величина тока в
, вызывает токи во всех ветвях произвольной линейной электрической цепи. Величина тока в 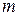 – ой ветви определяется из уравнения
– ой ветви определяется из уравнения
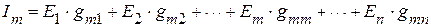
при равных нулю всех ЭДС, кроме 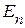 , т.е.
, т.е.
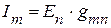 .
.
Откуда 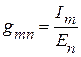 .
.
Таким образом, взаимная проводимость двух произвольных ветвей электрической цепи, определяется отношением тока 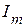 в одной ветви к ЭДС
в одной ветви к ЭДС 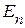 в другой ветви при равных нулю ЭДС источников напряжения в остальных ветвях схемы.
в другой ветви при равных нулю ЭДС источников напряжения в остальных ветвях схемы.
Из свойства взаимности следует равенство 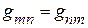 .
.
Входные и взаимные проводимости можно рассчитать или определить экспериментально.
Пример 2.20. Определение входных и взаимных проводимостей ветвей расчетным путем покажем на примере электрической цепи, рассмотренной в примере 2.15.
Из примера 2.15 , частичные токи от действия источника напряжения 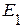 =20 В:
=20 В:
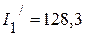 мА,
мА, 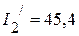 мА,
мА, 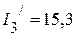 мА,
мА,
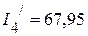 мА,
мА, 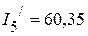 мА.
мА.
Частичные токи от действия источника напряжения 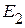 =15 В:
=15 В:
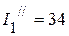 мА,
мА, 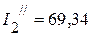 мА,
мА, 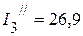 мА,
мА,
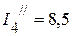 мА,
мА, 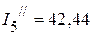 мА.
мА.
1. Входная проводимость 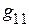 первой ветви равна отношению тока
первой ветви равна отношению тока 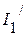 к ЭДС
к ЭДС 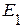 :
:
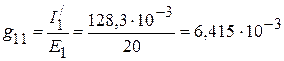 См.
См.
2. Взаимные проводимости между первой и остальными ветвями:
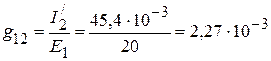 См,
См,
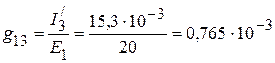 См,
См,
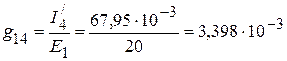 См,
См,
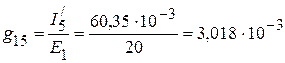 См.
См.
3. Входная проводимость 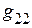 первой ветви равна отношению тока
первой ветви равна отношению тока 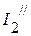 к ЭДС
к ЭДС 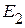 :
:
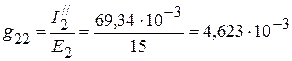 См.
См.
4. Взаимные проводимости между второй и остальными ветвями:
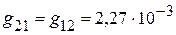 См,
См,
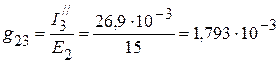 См,
См,
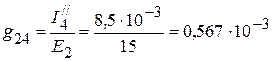 См,
См,
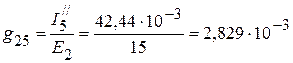 См.
См.
5. Используя принцип наложения, записываем уравнения, для нахождения токов в ветвях:
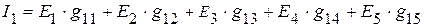 =
=
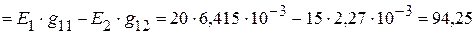 мА,
мА,
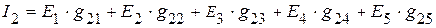 =
=
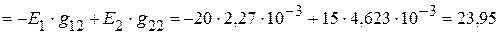 мА,
мА,
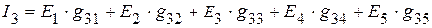 =
=
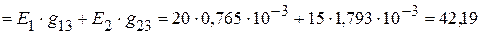 мА,
мА,
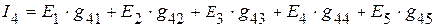 =
=
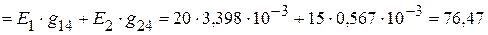 мА,
мА,
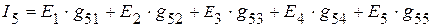 =
=
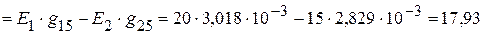 мА.
мА.
Токи в ветвях, рассчитанные в примерах 2.2 и 2.20, совпадают.
Активный трехполюсник
В разветвленных электрических цепях в ряде случаев нет необходимости рассчитывать токи во всех ветвях. Например, используя метод эквивалентного генератора, можно определить ток одной ветви произвольной схемы. В этом случае вся цепь может быть упрощена путём замены её отдельных частей схемами замещения на основе эквивалентных преобразований. Подобная замена может существенно упростить анализ и методы расчёта электрических цепей. В этой связи методы определения параметров эквивалентных схем замещения активного трёхполюсника актуальны.
Ниже предложены методики представления линейного активного трёхполюсника постоянного тока А, питающего произвольную линейную (пассивную или активную) цепь (рис. 2.60), эквивалентной схемой, которая может быть в виде соединения звездой или треугольником. Подобный подход позволяет оценивать состояние выделенной цепи, подсоединенной к активному трехполюснику.

Рисунок 2.60 – Исходная схема
Рассмотрим схему замещения при соединении звездой (рис. 2.61).
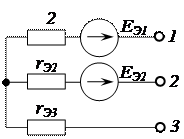
Рисунок 2.61 – Эквивалентная схема активного трёхполюсника при соединении звездой
В приведенной схеме необходимо определить параметры схемы замещения активных трехполюсников (эдс источников напряжения 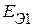 ,
, 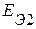 и сопротивлений
и сопротивлений 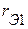 ,
, 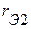 ,
, 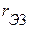 ).
).
Для нахождения ЭДС 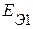 и
и 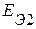 воспользуемся известным приёмом, используемым при определении ЭДС
воспользуемся известным приёмом, используемым при определении ЭДС 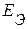 в методе эквивалентного генератора. С этой целью рассмотрим активный трехполюсник, к зажимам которого подсоединен произвольный пассивный трехполюсник. В режиме холостого хода, т.е. когда в исходной схеме (рис. 2.60) разомкнуты ветви 1 и 2, токи
в методе эквивалентного генератора. С этой целью рассмотрим активный трехполюсник, к зажимам которого подсоединен произвольный пассивный трехполюсник. В режиме холостого хода, т.е. когда в исходной схеме (рис. 2.60) разомкнуты ветви 1 и 2, токи 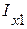 ,
, 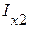 и
и 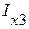 равны нулю (рис. 2.62 а). Если в разорванные зажимы 1, 1/ и 2, 2/ включить источники напряжения, ЭДС которых равны соответственно
равны нулю (рис. 2.62 а). Если в разорванные зажимы 1, 1/ и 2, 2/ включить источники напряжения, ЭДС которых равны соответственно 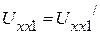 и
и 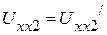 (рис. 2.62 б), то токи в полученной схеме будут также равны нулю. Включив в эти ветви такие же источники напряжения
(рис. 2.62 б), то токи в полученной схеме будут также равны нулю. Включив в эти ветви такие же источники напряжения 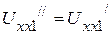 и
и 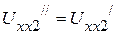 , но направленные встречно исходным (рис. 2.62 в), получаем схему, токи которой равны токам в исходной схеме. К полученной схеме применим принцип наложения. Частичные токи
, но направленные встречно исходным (рис. 2.62 в), получаем схему, токи которой равны токам в исходной схеме. К полученной схеме применим принцип наложения. Частичные токи 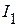 ,
, 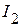 ,
, 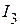 от действия всех источников питания активного трехполюсника и источников напряжения
от действия всех источников питания активного трехполюсника и источников напряжения 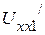 и
и 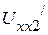 равны нулю. Тогда токи в выделенных ветвях будут определяться источниками напряжения
равны нулю. Тогда токи в выделенных ветвях будут определяться источниками напряжения 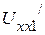 и
и 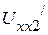 , а активный трехполюсник в этом случае заменяется пассивным. Таким образом, ЭДС эквивалентной схемы замещения (рис. 2.61) соответственно равны
, а активный трехполюсник в этом случае заменяется пассивным. Таким образом, ЭДС эквивалентной схемы замещения (рис. 2.61) соответственно равны 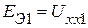 и
и 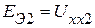 . Пассивные параметры трёхполюсника можно всегда представить эквивалентной звездой с сопротивлениями
. Пассивные параметры трёхполюсника можно всегда представить эквивалентной звездой с сопротивлениями 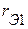 ,
, 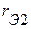 ,
, 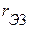 , представленной на рисунке 2.62 г.
, представленной на рисунке 2.62 г.
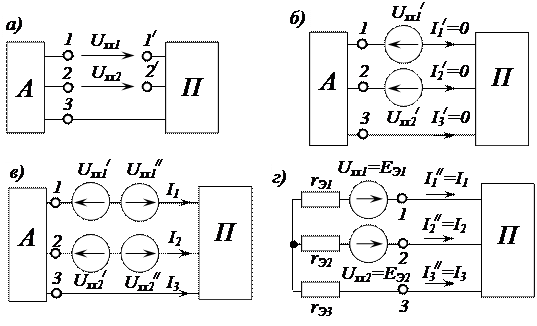
Рисунок 2.62 – Обоснование замены активного трёхполюсника эквивалентной схемой с пассивным трёхполюсником и источниками напряжения с ЕЭ1=Uxx1 и ЕЭ2=Uxx2
Рассмотрим возможность определения 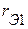 ,
, 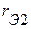 ,
, 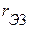 . Для этого необходимо определить входные сопротивления пассивного трёхполюсника относительно выводов 1-2 (
. Для этого необходимо определить входные сопротивления пассивного трёхполюсника относительно выводов 1-2 ( 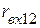 ), 2-3 (
), 2-3 ( 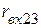 ), 1-3 (
), 1-3 ( 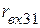 ), которые, соответственно, равны
), которые, соответственно, равны
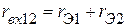 ;
;
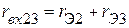 ;
;
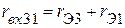 .
.
Тогда эквивалентные сопротивления 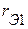 ,
, 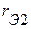 ,
, 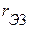 соответственно равны:
соответственно равны:
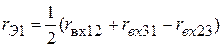 ;
;
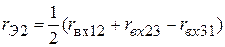 ;
;
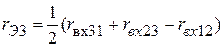 .
.
Величины входных сопротивлений пассивного трехполюсника могут быть определены расчетным путем и экспериментальным.
При расчетном определении входных сопротивлений, используют различные методы преобразования пассивных электрических цепей.
При определении входных сопротивлений по результатам эксперимента, необходимо, кроме опытов холостого хода (рис. 2.63), по результатам которого 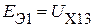 ,
, 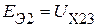 , необходимо провести три опята короткого замыкания.
, необходимо провести три опята короткого замыкания.
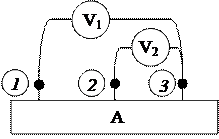
Рисунок 2.63 – Опыт холостого хода активного трехполюсника
На первом этапе, перемыкаются выводы 1-2 при разомкнутом выводе 3, затем перемыкаются выводы 1-3 при разомкнутом выводе 2 и, наконец, перемыкаются 2-3 при разомкнутом 1. Определяются токи короткого замыкания 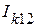 ,
, 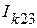 ,
, 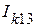 . Тогда входные сопротивления соответственно равны:
. Тогда входные сопротивления соответственно равны:
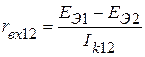 ;
;
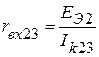 ;
;
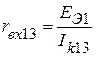 .
.
В случае, если опыты короткого замыкания недопустимы из-за больших значений токов короткого замыкания, вместо опыта короткого замыкания производится опыт нагрузки активного трёхполюсника на известное сопротивление r с измерением тока нагрузки Iн (рис. 2.64). Экспериментальные значения входных сопротивлений определяют по формулам:
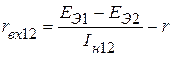 ;
;
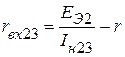 ;
;
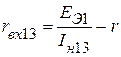 .
.
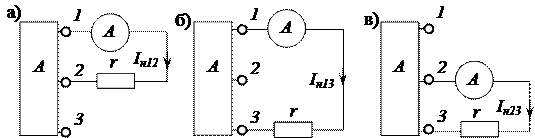
Рисунок 2.64 – Схема опытов под нагрузкой, используемых для
определения rЭ1, rЭ2 и rЭ3
Величины входных сопротивлений можно определить по результатам опытов холостого хода и короткого замыкания. Проведя последовательно опыты короткого замыкания относительно зажимов 1-2, 2-3 и 3-1, получим токи 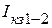 ,
, 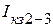 ,
, 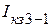 , а из опыта холостого хода - напряжения
, а из опыта холостого хода - напряжения 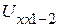 ,
, 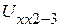 ,
, 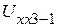 . Величины входных сопротивлений будут соответственно равны
. Величины входных сопротивлений будут соответственно равны
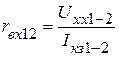 ;
; 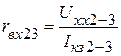 ;
; 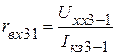 .
.
Величины 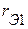 ,
, 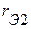 ,
, 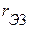 можно определить и другими методами. Так, при проведении опытов короткого замыкания относительно зажимов 1-2, кроме тока
можно определить и другими методами. Так, при проведении опытов короткого замыкания относительно зажимов 1-2, кроме тока 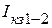 можно измерить напряжение
можно измерить напряжение 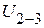 (рис. 2.65). Из эквивалентной схемы замещения активного трехполюсника следует
(рис. 2.65). Из эквивалентной схемы замещения активного трехполюсника следует
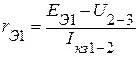 ;
; 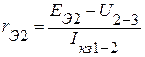 .
.
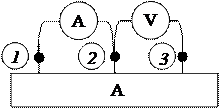
Рисунок 2.65 - Опыт короткого замыкания относительно
зажимов 1-2
По аналогии, при проведении опытов короткого замыкания относительно зажимов 2-3, измеряют напряжение 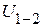 . В этом случае
. В этом случае
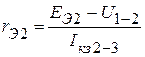 ;
; 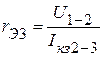 .
.
Пример 2.21. Рассмотрим основные свойства активных трехполюсников и методов определения параметров их схем замещения, на примере разветвленной электрической цепи, показанной на рисунке 2.66. Параметры приведенной цепи: E31 = 23,2 B, Е42 = 20 В, r14 = 300 Ом, r42 = 600 Ом, r34 = 900 Ом, r31 = 200 Ом, r12 = 150 Ом, r23 = 400 Ом, R1 = 50 Ом, R2 = 75 Ом, R3 = 100 Ом.
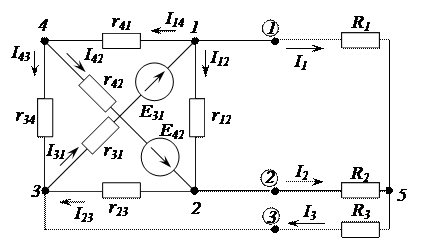
Рисунок 2.66 - Разветвленная электрическая цепь к пояснению
свойств активного трехполюсника
Данная схема состоит из пяти узлов 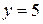 и девяти ветвей
и девяти ветвей 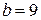 . При решении основной задачи расчета электрической цепи, например с применением законов Кирхгофа, необходимо составить и решить систему уравнений, равную количеству ветвей
. При решении основной задачи расчета электрической цепи, например с применением законов Кирхгофа, необходимо составить и решить систему уравнений, равную количеству ветвей 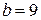 . При использовании метода контурных токов, необходимо составить и решить систему уравнений с
. При использовании метода контурных токов, необходимо составить и решить систему уравнений с 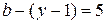 неизвестными контурными токами.При использовании метода узловых потенциалов, необходимо составить и решить систему уравнений с
неизвестными контурными токами.При использовании метода узловых потенциалов, необходимо составить и решить систему уравнений с 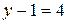 неизвестными потенциалами узлов приведенной схемы. Рассчитаем токи в ветвях приведенной схемы, с использованием свойств активных трехполюсников.
неизвестными потенциалами узлов приведенной схемы. Рассчитаем токи в ветвях приведенной схемы, с использованием свойств активных трехполюсников.
В общем случае в разветвленных цепях можно выделить звезду или треугольник, а остальную часть схемы представить в виде активного трехполюсника.
Так на схеме, приведенной на рисунке 2.66, выделены три ветви с резистивными сопротивлениями R1, R2, и R3, условно называемые нагрузкой. Остальная часть схемы может быть представлена активным трехполюсником (рис. 2.67 а). Активный трехполюсник может быть замещен эквивалентной схемой. В этом случае схема имеет вид, представленный на рисунке 2.67 б.
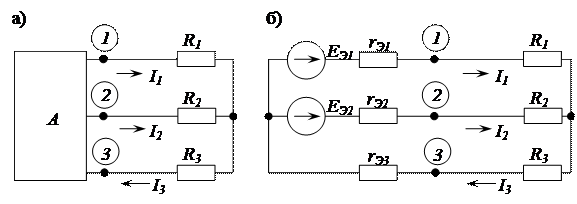
Рисунок 2.67 - Преобразование сложной электрической цепи с
выделением трехполюсника: а – схема с активным трехполюсником;
б – схема с заменой активного трехполюсника эквивалентной схемой
Приведенная схема была исследована расчетным путем и экпериментально.
Рассмотрим методы определения параметров схемы замещения активного трехполюсника 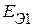 ,
, 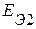 ,
, 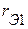 ,
, 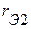 ,
, 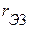 . На первом этапе используем расчетный метод.
. На первом этапе используем расчетный метод.
1. Определяем напряжения холостого хода активного трехполюсника 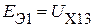 ,
, 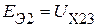 .
.
1.1. Удаляем из схемы сопротивления нагрузки R1 и R2 (разрываем ветвь) и вычерчиваем схему активного трехполюсника (2.68)
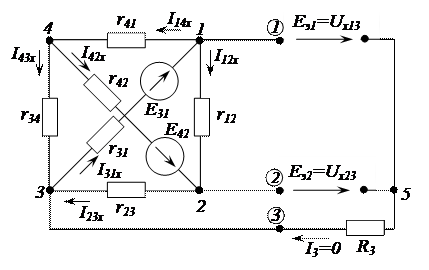
Рисунок 2.68 - Схема активного трехполюсника
1.2. Произвольным методом (МКТ, МУП и т.д.), определяем токи в схеме активного трехполюсника.
В приведенной на рисунке 2.69 схеме, для определение токов в ветвях, используем метод узловых потенциалов.
1.2.1. Осуществляем предварительный анализ схемы. Количество ветвей – 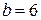 , количество узлов –
, количество узлов – 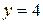 .
.
Потенциал четвертого узла принимаем равным нулю: 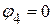 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 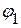 ,
, 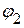 ,
, 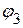 .
.
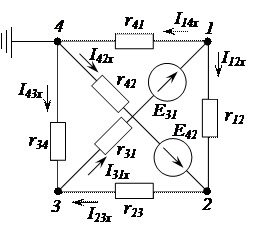
Рисунок 2.69 – Расчетная схема активного трехполюсника
1.2.2. Составляем уравнения для определения потенциалов 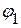 ,
, 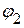 ,
, 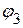 .
.
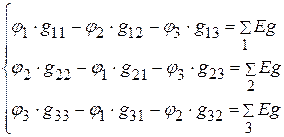 .
.
1.2.3. Подставляем числовые значения и решаем систему уравнений.
1.2.3.1. Проводимости ветвей
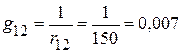 См;
См;
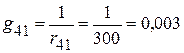 См;
См;
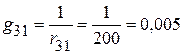 См;
См;
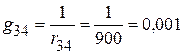 См;
См;
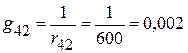 См;
См;
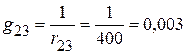 См.
См.
1.2.3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
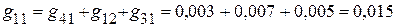 См;
См;
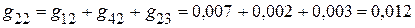 См;
См;
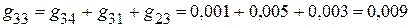 См.
См.
Сумма проводимостей, соединяющих различные узлы
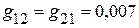 См;
См;
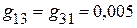 См;
См;
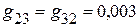 См.
См.
Узловые токи 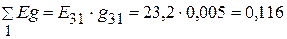 А,
А,
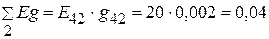 А,
А,
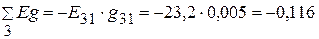 А.
А.
1.2.3.3. После подстановки цифровых данных система имеет вид
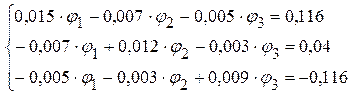
1.2.3.4. Решая данную систему уравнений произвольным методом, определяем потенциалы:
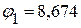 В,
В,
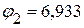 В,
В,
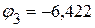 В.
В.
1.2.3.5. Определяем токи в ветвях электрической цепи, приведенной на рис. 2.69.
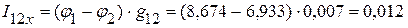 А,
А,
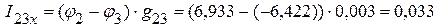 А,
А,
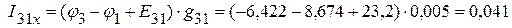 А,
А,
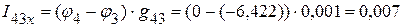 А,
А,
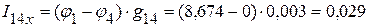 А,
А,
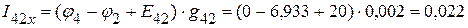 А.
А.
1.3. Используя второй закон Кирхгофа, определяем 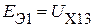 и
и 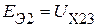 .
.
Из контура 15321 : 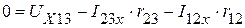
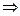
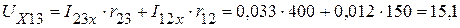 В.
В.
Из контура 5325 : 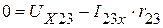
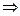
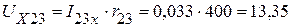 В.
В.
2. Определяем сопротивления эквивалентной схемы замещения 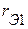 ,
, 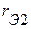 ,
, 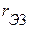 пассивного трехполюсника.
пассивного трехполюсника.
2.1. Из схемы активного трехполюсника удаляем источники питания и вычерчиваем схему пассивного трехполюсника (рис. 2.70).
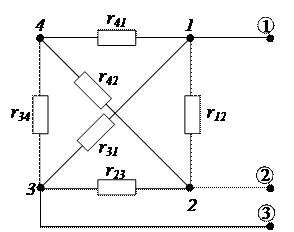
Рисунок 2-70 - Схема пассивного трехполюсника
2.1.1. Звезду из сопротивлений 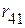 ,
, 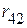 ,
, 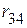 преобразовываем в треугольник сопротивлений (рис. 2.71 а).
преобразовываем в треугольник сопротивлений (рис. 2.71 а).
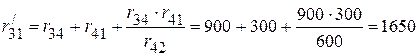 Ом;
Ом;
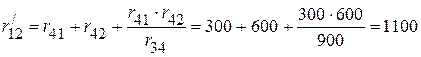 Ом;
Ом;
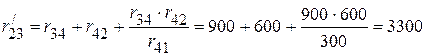 Ом.
Ом.
2.1.2. Параллельно соединенные сопротивления 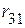 и
и 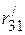 ,
, 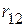 и
и 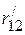 ,
, 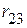 и
и 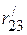 заменяем эквивалентными сопротивлениями (рис. 2.71 б).
заменяем эквивалентными сопротивлениями (рис. 2.71 б).
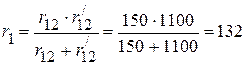 Ом;
Ом;
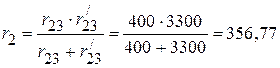 Ом;
Ом;
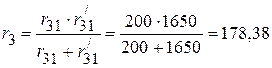 Ом.
Ом.
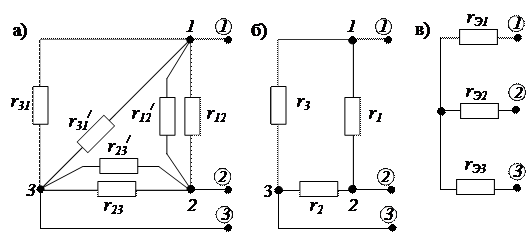
Рисунок 2.71 – Нахождение сопротивлений эквивалентной
схемы замещения
2.1.3. Определяем эквивалентные сопротивления 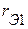 ,
, 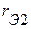 ,
, 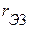 используя формулы перехода от треугольника сопротивлений к звезде сопротивлений (рис. 2.71 в).
используя формулы перехода от треугольника сопротивлений к звезде сопротивлений (рис. 2.71 в).
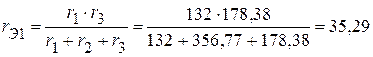 Ом;
Ом;
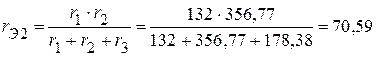 Ом;
Ом;
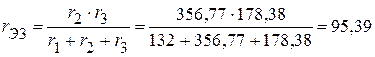 Ом.
Ом.
Приведенная на рисунке 2.68 схема, была собрана на стенде УИЛС-2, для подтверждения расчетного метода и с помощью эксперимента были определены параметры эквивалентной схемы замещения.
По результатам холостого хода были определены величины 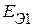 ,
, 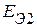 соответственно равные
соответственно равные
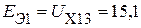 В,
В, 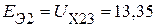 В.
В.
Величины входных сопротивлений были определены по результатам опытов холостого хода и короткого замыкания. Проведя последовательно опыты короткого замыкания относительно зажимов 1-2, 2-3 и 3-1, получим токи короткого замыкания:
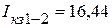 мА,
мА, 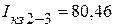 мА,
мА, 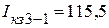 мА.
мА.
Проведя последовательно опыты холостого хода относительно зажимов 1-2, 2-3 и 3-1, получим напряжения холостого хода:
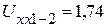 В,
В, 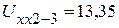 В,
В, 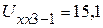 В.
В.
Тогда величины входных сопротивлений пассивного трехполюсника соответственно равны
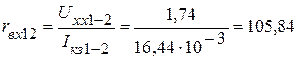 Ом;
Ом;
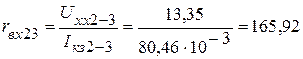 Ом;
Ом;
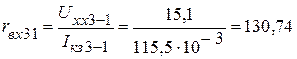 Ом.
Ом.
Следовательно, эквивалентные сопротивления 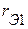 ,
, 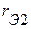 ,
, 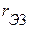 активного трехполюсника, равны:
активного трехполюсника, равны:
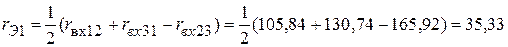 Ом;
Ом;
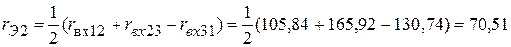 Ом;
Ом;
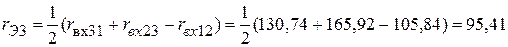 Ом.
Ом.
В таблице 1 приведены результаты параметров схемы замещения активного трехполюсника, по результатам эксперимента и расчета.
Таблица 1 - Параметры схемы замещения активного трехполюсника
| Параметры схемы замещения | ЕЭ1, В | ЕЭ2, В | rЭ1,Ом | rЭ2,Ом | rЭ3, Ом |
| Расчетным путем | 15,1 | 13,35 | 35,29 | 70,59 | 95,39 |
| Экспериментальным путем | 15,1 | 13,35 | 35,33 | 70,51 | 95,41 |
Из сравнения результатов расчета и экспериментов следует их практическая сходимость.
Параметры схемы замещения активного трехполюсника, позволяют определить токи нагрузки 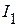 ,
, 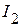 ,
, 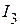 .
.
Вычерчиваем схему замещения активного трехполюсника (рис. 2.72) и определяем токи 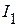 ,
, 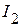 ,
, 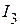 .
.
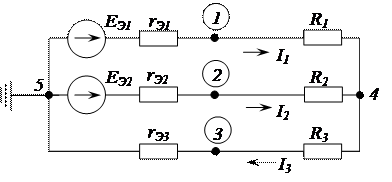
Рисунок 2.72 – Схема замещения активного трехполюсника
1. Осуществляем предварительный анализ схемы. Количество ветвей – 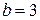 , количество узлов –
, количество узлов – 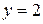 .
.
Потенциал пятого узла принимаем равным нулю: 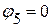 . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал 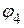 .
.
2. Составляем уравнение для определения потенциала 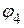 :
:
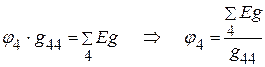 .
.
3. Подставляем числовые значения и находим потенциал 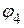 .
.
3.1. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
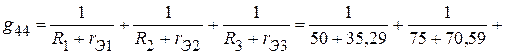
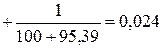 См;
См;
Узловые токи
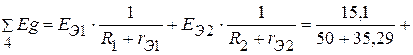
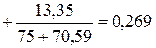 А.
А.
3.2. После подстановки цифровых значений, определяем потенциал 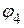 :
: 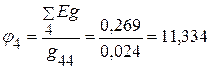 В.
В.
3.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.72.
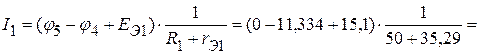
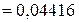 А,
А,
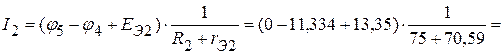
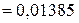 А,
А,
 А.
А.
Величины токов нагрузки по результатам эксперимента соответственно равны 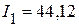 мА,
мА, 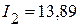 мА,
мА, 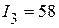 мА.
мА.
В таблице 2 приведены результаты значений токов нагрузки, по результатам эксперимента и расчета.
Таблица 2 - Результаты значений токов нагрузки
| Токи нагрузки | I1, мA | I2, мA | I3,мA |
| Расчетным путем | 44,16 | 13,85 | 58,01 |
| Экспериментальным путем | 44,12 | 13,89 | 58,0 |
Из сравнения результатов расчета и экспериментов следует их практическая сходимость.
Полученные результаты электрического состояния токов нагрузки на элементах, позволяют путем использования законов Кирхгофа определить токи в ветвях активного трехполюсника.
Используя законы Кирхгофа, определяем токи в ветвях активного трехполюсника, представленного на рисунке 2.66.
1. Используя второй закон Кирхгофа, определяем токи 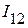 ,
, 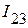 и
и 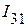 :
:
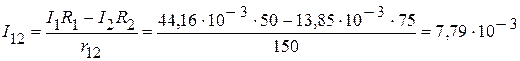 А;
А;
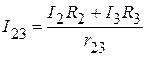
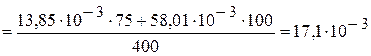 А;
А;
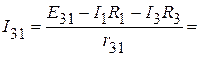
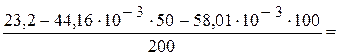
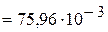 А.
А.
2. Используя первый закон Кирхгофа, определяем токи в оставшихся ветвях 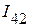 ,
, 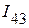 и
и 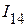 . Они соответственно равны:
. Они соответственно равны:
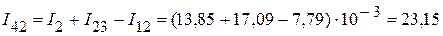 мА;
мА;
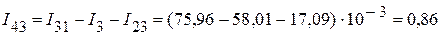 мА;
мА;
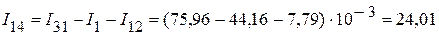 мА.
мА.
Величины токов в ветвях по результатам эксперимента соответственно равны
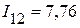 мА,
мА, 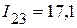 мА,
мА, 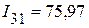 мА,
мА,
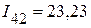 мА;
мА; 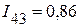 мА;
мА; 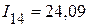 мА.
мА.
В таблице 3 приведены результаты значений токов нагрузки, по результатам эксперимента и расчета.
Таблица 3 - Величины токов в ветвях активного трехполюсника
| Токи в ветвях активного трехполюсника | I12, мА | I23, мА | I31, мА | I42, мА | I43, мА | I14, мА |
| Расчетным путем | 7,79 | 17,1 | 75,96 | 23,15 | 0,86 | 24,01 |
| Экспериментальным путем | 7,76 | 17,1 | 76,97 | 23,23 | 0,86 | 24,09 |
Из сравнения результатов расчета и экспериментов следует их практическая сходимость.
Свойства активных трехполюсников можно применить и для электрических схем с более сложной топографией. В качестве примера на рисунке 2.73 представлена разветвленная электрическая цепь, состоящая из 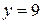 узлов и
узлов и 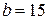 ветвей. Ее особенностью является тот факт, что S сечение I-II, проведенное через ветви с резистивными сопротивлениями
ветвей. Ее особенностью является тот факт, что S сечение I-II, проведенное через ветви с резистивными сопротивлениями 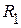 ,
, 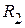 ,
, 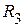 разбивает приведенную схему на два активных трехполюсника, приведенных на рисунке 2.75 а. Используя известные приемы, заменим активные трехполюсники
разбивает приведенную схему на два активных трехполюсника, приведенных на рисунке 2.75 а. Используя известные приемы, заменим активные трехполюсники 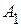 и
и 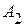 пассивными
пассивными 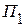 и
и 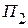 , введя в ветви с токами
, введя в ветви с токами 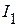 и
и 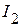 напряжения
напряжения 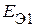 ,
, 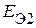 , соответственно равные
, соответственно равные 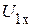 и
и 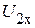 (рис. 2.74).
(рис. 2.74).
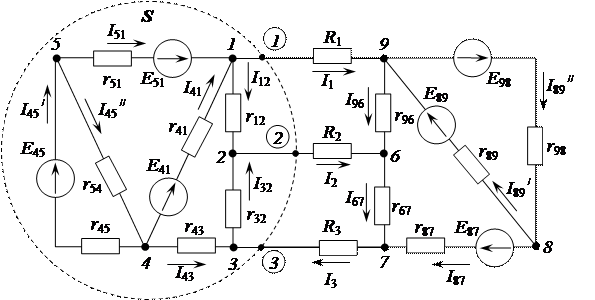
Рисунок 2.73 - Сложная разветвленная электрическая цепь
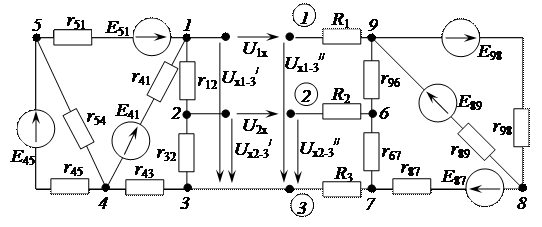
Рисунок 2.74 - Электрическая цепь с напряжениями холостого хода
Необходимо отметить, что 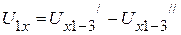 , а
, а 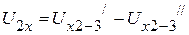 . Следовательно,
. Следовательно, 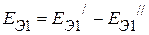 , а
, а 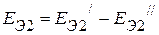 . Здесь,
. Здесь, 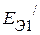 и
и 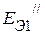 – эдс источников напряжения схемы замещения первого активного трехполюсника, а
– эдс источников напряжения схемы замещения первого активного трехполюсника, а 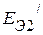 и
и 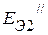 – второго. Используя вышеуказанную методику, пассивные трехполюсники заменяем схемами в виде звезды. В результате получим схему, приведенную на рисунке 2.75 б. Здесь
– второго. Используя вышеуказанную методику, пассивные трехполюсники заменяем схемами в виде звезды. В результате получим схему, приведенную на рисунке 2.75 б. Здесь 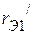 ,
, 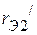 и
и 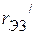 - эквивалентные сопротивления пассивного трехполюсника
- эквивалентные сопротивления пассивного трехполюсника 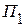 , полученного из активного
, полученного из активного 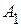 ;
; 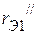 ,
, 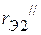 и
и 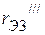 - эквивалентные сопротивления пассивного трехполюсника
- эквивалентные сопротивления пассивного трехполюсника 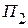 , полученного из активного
, полученного из активного  .
.
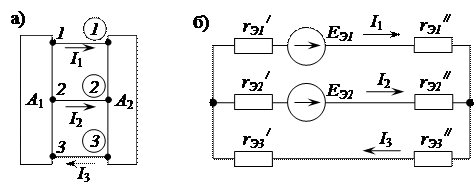
Рисунок 2.75 - Эквивалентная схема разветвленной цепи с двумя
активными трехполюсниками
а – схема, цепи с двумя активными трехполюсниками А1, А2;
б – схема замещения
Таким образом, результирующая эквивалентная схема замещения, приведенная на рисунке 2.75 б, является результатом сложения эквивалентных схем замещения первого и второго активных трехполюсников (рис. 2.76).
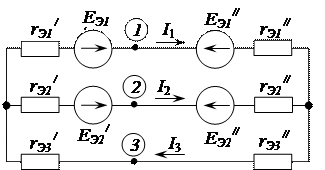
Рисунок 2.76 - Формирование эквивалентной схемы замещения электрической цепи с двумя активными трехполюсниками
Полученные результаты позволяют рассчитать токи в ветвях первого и второго активных трехполюсников. При расчете токов первого активного трехполюсника используем эквивалентную схему замещения второго активного трехполюсника (рис. 2.77).
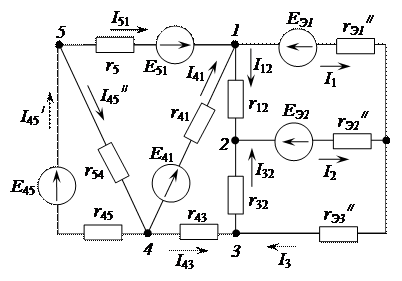
Рисунок 2.77 - Схема для определения токов
первого активного трехполюсника
Применяя второй закон Кирхгофа, определяем токи 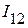 ,
, 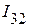 :
:
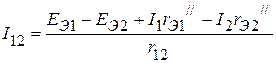 ;
; 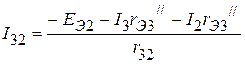 .
.
Из первого закона Кирхгофа для узла 3, имеем:
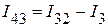 .
.
Используя второй закон Кирхгофа для контура 12341, определяем ток 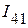 :
:
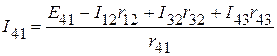 .
.
Применяя первый закон Кирхгофа для узла 1, определяем ток 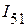 :
:
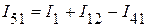 .
.
По второму закону Кирхгофа определяем ток 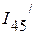 ,
, 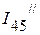 :
:
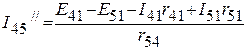 ;
; 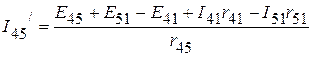 .
.
При расчете токов второго активного трехполюсника используем схему замещения первого активного трехполюсника (рис. 2.78).
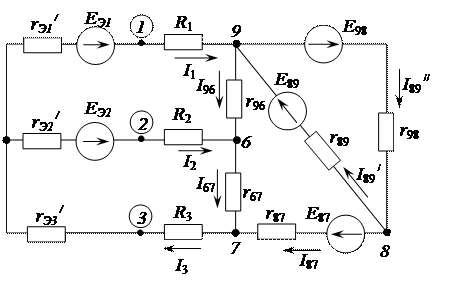
Рисунок 2.78 - Схема для определения токов второго
активного трехполюсника
Применяя второй закон Кирхгофа, определяем токи 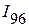 ,
, 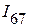 :
:
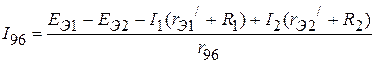 ;
; 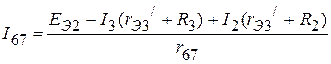 .
.
Из первого закона Кирхгофа для узла 7, имеем:
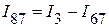 .
.
По второму закону Кирхгофа определяем ток 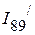 ,
, 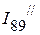 :
:
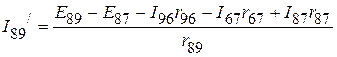 ;
; 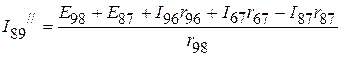 .
.
Таким образом, используя свойства активного трехполюсника, первый и второй законы Кирхгофа, были определены токи во всех ветвях разветвленной электрической цепи.
Предложенная методика расчета и анализа электрических цепей, основанная на использовании свойствактивных трехполюсников, позволяет расширить возможности анализа электрического состояния различных частей разветвленных электрических цепей. Метод применим при анализе схем с неизвестной топографией трехполюсников по результатам входных параметров.
