Классификация поточных шифров

Билет 15

Одно-ключевые (симметричные) шифры –криптографические алгоритмы процессы за- и расшифровывание в которых отличаются лишь порядком выполнения и направлением некоторых простых шагов (в отличие асимметричных или

алгоритмов с открытым ключом). Особенности симметричных шифров:

• каждый из участников обмена может как

зашифровать, так и расшифровать сообщение;

• необходима специальная служба для изготовления и

доставки секретных ключей;

• позволяют защищать сообщения от прочтения и

некоторых видов модификации.

• не позволяют подтверждать или опровергать

авторство сообщений.

Условия стойкости блочного шифра (по К.Шеннону) :

• рассеивание – один бит исходного текста должен влиять

на несколько битов шифротекста, оптимально — на все

биты в пределах одного блока. При шифровании двух

блоков данных с минимальными отличиями между ними

должны получаться совершенно непохожие друг на друга

блоки шифротекста. Аналогично и для зависимости

шифротекста от ключа—один бит ключа должен влиять на

несколько битов шифротекста;

• перемешивание – шифр должен скрывать зависимости

между символами исходного текста и шифротекста. Если

шифр достаточно хорошо «перемешивает» биты исходного

текста, то соответствующий шифротекст не содержит

никаких статистических, и, тем более, функциональных

закономерностей.

Условия стойкости

Если шифр обладает обоими указанными свойствами, то любые изменения в блоке открытых данных приведут к тому, что все биты в зашифрованном блоке данных с вероятностью ½ независимо друг от друга та же поменяют свои значения.

Такой шифр невозможно вскрыть способом, менее затратным с точки зрения количества необходимых операций, чем полный перебор по множеству

возможных значений ключа.

Билет 16

Блочный шифр — разновидность симметричного шифра[1], оперирующего группами бит фиксированной длины — блоками, характерный размер которых меняется в пределах 64‒256 бит. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Фактически, блочный шифр представляет собой подстановку на алфавите блоков, которая, как следствие, может быть моно- или полиалфавитной.[2] Блочный шифр является важной компонентой многих криптографических протоколов и широко используется для защиты данных, передаваемых по сети.

Блочный шифр за один прием обрабатывает блок открытого текста.

Основное отличие блочного шифра от поточного состоит в том, что поточным шифрам необходимо постоянно помнить о том, какое место битовой строки они в данный момент обрабатывают, чтобы определить, какую часть ключевого потока нужно сейчас генерировать; блочные же шифры избавлены от этой необходимости.

Размер блока р,ля шифрования обычно выбирают разумно боль­

шим. В системе DBS (стандарт шифрования данных), например, Глава 5.

Сегодня принято на вооружение довольно много разновидностей

блочных шифров, некоторые из которых с большой долей вероятно­

сти используются Вашим web-браузером: RC5, RC6, DBS или 3DES.

Наиболее знаменитый из них — DES^ т.е. стандарт шифрования

данных. Впервые он был опубликован в середине семидесятых го­

дов XX века как федеральный стандарт США и вскоре оказался, де-

факто, международным стандартом в банковских операциях. DES

успешно выдержал испытание временем, но к началу 90-ых годов

назрела необходимость в разработке новых стандартов. Произошло

это потому, что как длина блока (64 бита), так и размер ключа (56

битов) оригинального алгоритма DES оказались недостаточными

Лля обеспечения секретности сообщений. В настоящее время можно

восстановить 56-битовый ключ системы DES., используя либо сеть

компьютеров, либо специализированные аппаратные средства ЭВМ.

В ответ на эту проблему национальный институт стандартов и тех­

нологий США (NIST) положил начало своего рода соревнованию по

поиску нового блочного шифра, достойного названия «новый стан­

дарт шифрования» [AES).

В отличие от фактически засекреченных работ над про

Архитектура… Шифр обычно составляют из более простых

шифрующих преобразований. Простое шифрующие

преобразование – преобразование, которое реализуется

аппаратно относительно несложной логической схемой

или программно несколькими компьютерными

командами.

Основные шифрующие преобразования:

• перестановка (permutation) – перестановка

структурных элементов шифруемого блока

данных (битов, символов, цифр);

• замена, подстановка (substitution) – замена группы

элементов шифруемого блока на другую группу по

индексной таблице;

• функциональное преобразование (function) –

различные сдвиги, логические и арифметические

операций.

Билет 17

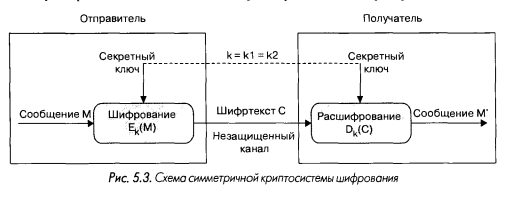
Исторически первыми появились симметричные криптографические системы.

В симметричной криптосистеме шифрования используется один и тот же ключ для

зашифрования и расшифрования информации. Это означает, что любой, кто име­

ет доступ к ключу шифрования, может расшифровать сообщение. Соответственно,

с целью предотвращения несанкционированного раскрытия зашифрованной ин­

формации все ключи шифрования в симметричных криптосистемах должны держать­

ся в секрете. Именно поэтому симметричные криптосистемы называют криптосисте­

мами с секретным ключом - ключ шифрования должен быть доступен только тем,

кому предназначено сообщение. Симметричные криптосистемы называют еще од­

ноключевыми криптографическими системами или криптосистемами с закрытым

ключом. Схема симметричной криптосистемы шифрования показана на рис. 5.3.

Данные криптосистемы характеризуются наиболее высокой скоростью шифро­

вания, и с их помощью обеспечивается как конфиденциальность и подлинность, так

и целостность передаваемой информации [29].

Конфиденциальность передачи информации с помощью симметричной крипто­

системы зависит от надежности шифра и обеспечения конфиденциальности ключа

шифрования. Обычно ключ шифрования представляет собой файл или массив

данных и хранится на персональном ключевом носителе, например дискете или

смарт-карте; обязательно принятие мер, обеспечивающих недоступность персональ­

ного ключевого носителя кому-либо, кроме его владельца.

Подлинность обеспечивается за счет того, что без предварительного расшифро­

вывания практически невозможно осуществить смысловую модификацию и под­

лог криптографически закрытого сообщения. Фальшивое сообщение не может

быть правильно зашифровано без знания секретного ключа.

Целостность данных обеспечивается присоединением к передаваемым данным

специального кода (имитовставки), вырабатываемой по секретному ключу. Ими-

товставка является разновидностью контрольной суммы, то есть некоторой эталон­

ной характеристикой сообщения, по которой осуществляется проверка целостности

последнего. Алгоритм формирования имитовставки должен обеспечивать ее зави

симость по некоторому сложному криптографическому закону от каждого бит

сообщения. Проверка целостности сообщения выполняется получателем сообщ

ния путем выработки по секретному ключу имитовставки, соответствующей пол

ченному сообщению, и ее сравнения с полученным значением имитовставки. Пр

совпадении делается вывод о том, что информация не была модифицирована н

пути от отправителя к получателю.

Симметричное шифрование идеально подходит в случае шифрования инфор

мации «для себя», например, с целью предотвратить несанкционированный досту

к ней в отсутствие владельца. Это может быть как архивное шифрование выбран

ных файлов, так и прозрачное (автоматическое) шифрование целых логически

или физических дисков.

Обладая высокой скоростью шифрования, одноключевые криптосистемы позво

ляют решать многие важные задачи защиты информации. Однако автономное и

пользование симметричных криптосистем в компьютерных сетях порождает про

блему распределения ключей шифрования между пользователями.

Билет 18

Потоковый шифр - вид шифра, в котором каждый бит данных зашифровывается посредством гаммирования. Процесс гаммирования подразумевает наложение на информацию гамм кода по строго определенным правилам. Чтобы расшифровать данные, требуется наложение той же гаммы на зашифрованный текст.

Первые потоковые шифры были использованы еще во времена Второй мировой войны (до появления электроники). Более чем через два десятка лет (в 1965 году) норвежский криптограф Эранст Селмер разработал свою теорию последовательности регистровых сдвигов. Еще через время Соломон Голомб написал книгу о последовательности сдвиговых регистров. При этом популярность потоковым шифрам пришла раньше - в 1949 году, когда миру была представлена работа Клода Шеннона о стойкости шифра Вернама.

Принцип потокового шифрования. Генератор случайных чисел выдает определенную гамму (числовую последовательность). Последняя накладывается на шифруемую информацию с применением операции XOR. На выходе получаются зашифрованные данные. Наиболее популярный потоковый шифр - RC4, признанный органами стандартизации. Надежность потокового шифрования зависит от числовой последовательности, выдаваемой генератором.

Сфера применения потоковых шифров - военные, сетевые, телефонные и другие системы, где необходимо преобразование речевой информации в цифровую форму и надежное шифрование данных. Причина популярности - простота реализации и конструирования генераторов, надежность шифрования, отсутствие ошибок в потоковом шифре.

Классификация поточных шифров

Допустим, например, что в режиме гаммирования для поточных шифров при передаче по каналу связи произошло искажение одного знака шифротекста. Очевидно, что в этом случае все знаки, принятые без искажения, будут расшифрованы правильно. Произойдёт потеря лишь одного знака текста. А теперь представим, что один из знаков шифротекста при передаче по каналу связи был потерян. Это приведёт к неправильному расшифрованию всего текста, следующего за потерянным знаком. Практически во всех каналах передачи данных для поточных систем шифрования присутствуют помехи. Поэтому для предотвращения потери информации решают проблему синхронизации шифрования и расшифрования текста. По способу решения этой проблемы шифр системы подразделяются на синхронные и системы с самосинхронизацией.

Синхронные поточные шифры (СПШ) — шифры, в которых поток ключей генерируется независимо от открытого текста и шифро текста.

При шифровании генератор потока ключей выдаёт биты потока ключей, которые идентичны битам потока ключей при дешифровании. Потеря знака шифротекста приведёт к нарушению синхронизации между этими двумя генераторами и невозможности расшифрования оставшейся части сообщения. Очевидно, что в этой ситуации отправитель и получатель должны повторно синхронизоваться для продолжения работы.

Обычно синхронизация производится вставкой в передаваемое сообщение специальных маркеров. В результате этого пропущенный при передаче знак приводит к неверному расшифрованию лишь до тех пор, пока не будет принят один из маркеров.

Заметим, что выполняться синхронизация должна так, чтобы ни одна часть потока ключей не была повторена. Поэтому переводить генератор в более раннее состояние не имеет смысла.

Самосинхронизирующиеся поточные шифры (асинхронные поточные шифры (АПШ)) – шифры, в которых поток ключей создаётся функцией ключа и фиксированного числа знаков шифротекста.

Итак, внутреннее состояние генератора потока ключей является функцией предыдущих N битов шифротекста. Поэтому расшифрующий генератор потока ключей, приняв N битов, автоматически синхронизируется с шифрующим генератором.

Реализация этого режима происходит следующим образом: каждое сообщение начинается случайным заголовком длиной N битов; заголовок шифруется, передаётся и расшифровывается; расшифровка является неправильной, зато после этих N бит оба генератора будут синхронизированы

Анализировать потоковые шифры часто проще, чем блочные. Например, важным параметром, используе­мым для анализа генераторов на базе LFSR, является линейная сложность(linear complexity), или линейный интервал. Она определяется как длина п самого короткого LFSR, который может имитировать выход генерато­ра. Любая последовательность, генерированная конечным автоматом над конечным полем, имеет конечную линейную сложность [1006]. Линейная сложность важна, потому что с помощью простого алгоритма, называ е-мого алгоритмом Berlekamp-Massey,можно определить этот LFSR, проверив только 2и битов потока ключей [1005]. Воссоздавая нужный LFSR, вы взламываете потоковый шифр.

Билет 19

Объясним более четко, что такое арифметика остатков. Прежде

всего мы фиксируем положительное натуральное число iV, которое

называется модулем. Если разность двух целых чисел Ь — а делится

на N нацело, то пишут а = b (modN) и говорят, что числа а и 6

сравнимы по модулю iV. Очевидно, что в этом случае числа а и b

имеют один и тот же остаток^ от деления на N. Часто мы будем

лениться и писать просто а = Ь^ если ясно по какому модулю N

происходит сравнение.

Кроме того, мы будем использовать (modN) как обозначение

оператора модуля на множестве целых чисел, который вычисляет

наименьшее натуральное число, сравнимое с данным по модулю N.

Например,

18 (mod 7) = 4, -18 (mod 7) = 3.

Оператор модуля похож на оператор % в языке программирования

С, за тем исключением, что в нашей книге значения этого оператора

обычно неотрицательны. Например, в языках С или Java оператор

модуля действует так:

(-3)У,2=-1,

а мы будем полагать, что (—3) (mod 2) = 1.

Все возможные остатки от деления чисел на N образуют множе­

ство

Z/NZ= {О, ... , 7V-1} .

Очевидно, Z/NZ — множество значений оператора модуля (mod N).

Заметим, что некоторые авторы обозначают это множество через

ZAT. Тем не менее в этой книге мы будем придерживаться обозначе­

ния Z/7VZ. Еш;е раз отметим, что любой элемент множества Z/iVZ —

это остаток от деления некоторого числа на N. Поскольку все срав­

нимые между собой по модулю N целые числа имеют один и тот

же остаток, мы можем считать, что элемент х G Z/iVZ изображает

целый класс чисел вида х + kN^ где А : G Z. Таким образом, оперируя

с целыми числами по модулю 7V, мы будем считать все сравнимые

между собой числа равными друг другу и использовать традицион­

ный знак «= » вместо « =».

На множестве Z/iVZ есть две основных операции — сложение и

умножение. Они определяются обычным путем, например,

(11 + 13) (mod 16) = 24 (mod 16) = 8,

^Отсюда название «арифметика остатков». — Прим. перев. Глава 1. Сравнения^ группы, конечные поля и вероятность

так как 24 = 1 • 16 + 8, и

(11 • 13) (mod 16) = 143 (mod 16) = 15,

поскольку 143 = 8-16 + 15.

(Малая теорема Ферма.) Предположим, что число

р простое и а G F*; тогда

а^ = 1 (modp).

Функция Эйлера

Одна из центральных задач арифметики остатков — это решение

уравнения

а • X = b (modiV),

т. е. поиск элемента х G Z/A/'Z, удовлетворяющего этому равенству.

Линейное уравнение ах = b с вещественными коэффициентами при

а 7 ^ О всегда разрешимо. Если же рассматривать его над кольцом

целых чисел, то ответ найдется не всегда. Например, не суш;ествует

целого числа ж, обраш;ающего уравнение 2г г = 5 в верное равенство.

Случай же кольца вычетов еш;е более сложный, а потому и интерес­

ный с любой точки зрения. Действительно, суш;ествует ровно одно

решение уравнения

7-д: = 3 (mod 143),

уравнение

11-ж = 3 (mod 143)

решений не имеет, в то время как множество решений уравнения

11. ^ = 22 (mod 143)

насчитывает 11 элементов. Таким образом, встает вопрос: при ка­

ких условиях на а, 6 и Л Г уравнение ах = b (mod N) имеет решения

и как их все найти?

К счастью, существует очень простой критерий, позволяюш;ий

определить, имеет ли данное уравнение ни одного, одно или много

решений. Мы просто вычисляем наибольший общий делитель чисел

аиМ: Н0Д(а,7У).

- Если НОД (а, 7V) = 1, то существует ровно одно решение. Оно

может быть найдено с помощью промежуточного числа с, удо­

влетворяющего уравнению а-с = 1 (modiV), после чего искомое

неизвестное х вычисляется по формуле х = b - с (modiV).

- Если НОД {а^ N) ^ 1 и д = НОД (а, N) делит 6, то уравнение

будет иметь д решений. Чтобы их найти, нужно разделить

исходное уравнение на д:

а' -х' = Ь' (modiV'),

где а' = | , 6' = I и ЛГ' = ^ . Если ж' — решение полученного

уравнения, то решение исходного — любое число вида

X x' + i- N'

где г = 0, 1, ... , ^ - 1.

- В других случаях решений нет.

Ситуация, когда НОД(а,Л^) = 1, настолько важна, что А^ЛЯ нее

вводится специальное название. Говорят, что числа а и N взаимно

просты.

Число элементов кольца Z/7VZ, взаимно простых с 7V, дается

функцией Эйлера (р и равно ^{N). Значение (p{N) можно найти по

разложению числа N на простые множители. Если

где Pi — различные простые числа, то

v'W = ПРГЧР» -1).

Заметим, что последнее утверждение очень важно с точки зре­

ния криптографии: по разлоэюению числа N на простые множите­

ли легко вычислить значение (f{N). Особый интерес представляют

следующие частные случаи:

1. Если р простое, то

ip{p) =р-1.

2. Если р и q — простые числа и р ^ q^ то

(p{p'q) = {p-l){q-l).

Теорема 1.5. (Малая теорема Ферма.) Предположим, что число

р простое и а G F*; тогда

а^ = 1 (modp).

Малая теорема Ферма является частным случаем теоремы Ла­

гранжа и служит основой одного из тестов на простоту, который

будет рассматриваться в следующих главах.

Малая теорема Ферма может быть использована для тестирования числа на простоту: если ( a p − a ) {\displaystyle (a^{p}-a)} не делится на p {\displaystyle p} , то p — составное число. Однако обращение малой теоремы Ферма в общем случае неверно: если a {\displaystyle a} и p {\displaystyle p} — взаимно простые числа и a p − 1 − 1 {\displaystyle a^{p-1}-1} делится на p, то число p {\displaystyle p} может быть как простым, так и составным. В случае, когда p {\displaystyle p} является составным, оно называется псевдопростым Ферма по основанию a.

К примеру, китайская гипотезаruen утверждает, что p {\displaystyle p} является простым числом тогда и только тогда, когда 2 p ≡ 2 ( mod p ) {\displaystyle 2^{p}\equiv 2{\pmod {p}}} [19]. Здесь прямое утверждение о том, что если p {\displaystyle p} простое, то 2 p ≡ 2 ( mod p ) {\displaystyle 2^{p}\equiv 2{\pmod {p}}} , является частным случаем малой теоремы Ферма. Обратное же утверждение о том, что если 2 p ≡ 2 ( mod p ) {\displaystyle 2^{p}\equiv 2{\pmod {p}}} , то p {\displaystyle p} простое, есть частный случай обращения малой теоремы Ферма. Это обращение ложно: Саррус в 1820 году нашёл, что число N = 2 341 − 1 − 1 {\displaystyle N=2^{341-1}-1} делится на 341 {\displaystyle 341} , так как N {\displaystyle N} делится на 2 10 − 1 = 3 ⋅ 341 {\displaystyle 2^{10}-1=3\cdot 341} . Однако 341 {\displaystyle 341} — составное число: 341 = 11 ⋅ 31 {\displaystyle 341=11\cdot 31} . Таким образом, 341 — псевдопростое число по основанию 2[20].

В общем случае обращение малой теоремы Ферма также не выполняется. Контрпримером в общем случае являются числа Кармайкла: это числа p, являющиеся псевдопростыми по основанию a для всех a, взаимно простых с p. Наименьшим из чисел Кармайкла является 561.

Ввиду того, что обращение малой теоремы Ферма неверно, выполнение её условия не гарантирует что p — простое число. Тем не менее, малая теорема Ферма лежит в основе теста Ферма на простоту^[21]. Тест Ферма является вероятностным тестом на простоту: если теорема не выполняется, то число точно составное, а если выполняется — то число простое с некоторой вероятностью. Среди других вероятностных методов можно отметить: тест Соловея — Штрассена и тест Миллера — Рабина, последний в некоторой степени опирается на малую теорему Ферма^[22]. Также существует и детерминированный алгоритм: Тест Агравала — Каяла — Саксены.

Кроме того, справедливы следующие два утверждения. Если пара (2, n) удовлетворяют сравнению a n − 1 ≡ 1 ( mod n ) {\displaystyle a^{n-1}\equiv 1{\pmod {n}}} , то и пара чисел ( 2 , 2 n − 1 ) {\displaystyle (2,2^{n}-1)} также ему удовлетворяют. Для любого простого числа n и любого a > 2 такого, что ( a 2 − 1 , n ) = 1 {\displaystyle (a^{2}-1,n)=1} , значение a 2 n − 1 a 2 − 1 {\displaystyle {\frac {a^{2n}-1}{a^{2}-1}}} является псевдопростым числом Ферма по основанию a^[23].

Малая теорема Ферма также используется при доказательстве корректности алгоритма шифрования RSA^[2].

Билет 20

Билет 21

Асимметричная криптография изначально задумана как средство передачи сообщений от одного объекта к другому (а не для конфиденциального хранения информации, которое обеспечивают только симметричные алгоритмы). Поэтому дальнейшее объяснение мы будем вести в терминах "отправитель" – лицо, шифруюшее, а затем отпраляющее информацию по незащищенному каналу и "получатель" – лицо, принимающее и восстанавливающее информацию в ее исходном виде. Основная идея асимметричных криптоалгоритмов состоит в том, что для шифрования сообщения используется один ключ, а при дешифровании – другой.

Кроме того, процедура шифрования выбрана так, что она необратима даже по известному ключу шифрования – это второе необходимое условие асимметричной криптографии. То есть, зная ключ шифрования и зашифрованный текст, невозможно восстановить исходное сообщение – прочесть его можно только с помощью второго ключа – ключа дешифрования. А раз так, то ключ шифрования для отправки писем какому-либо лицу можно вообще не скрывать – зная его все равно невозможно прочесть зашифрованное сообщение. Поэтому, ключ шифрования называют в асимметричных системах "открытым ключом", а вот ключ дешифрования получателю сообщений необходимо держать в секрете – он называется "закрытым ключом".

Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в компьютере. Каждый пользователь в сети имеет свой пароль. При входе он указывает имя и вводит секретный пароль. Но если хранить пароль на диске компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции f {\displaystyle f} (АЛИСА_ГЛАДИОЛУС), пусть результатом будет строка РОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:

Имя	f {\displaystyle f} (имя_пароль)
АЛИСА	РОМАШКА
БОБ	НАРЦИСС

Вход в систему теперь выглядит так:

Имя:	АЛИСА
Пароль:	ГЛАДИОЛУС

Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к АЛИСА_ГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция практически необратимая.