Обработка результатов измерений

Обработать измерения- это значит извлечь сведения об интересующем нас предмете или явлении.

Иногда обработка производится с целью проверки той или иной статистической гипотезы в отношении изучаемого явления. Однако, чаще всего целью обработки является определение значений ряда физических параметров, характеризующий объект наблюдения. Иногда целью обработки является определение параметров измерительной аппаратуры, например систематических ошибок измерений.

При обработке косвенных измерений обычно имеются два этапа: 1)определение параметров по минимуму данных и

2)обработка избыточных измерений, при этом математическим объектом исследований является фундаментальная система измерений.

………………………

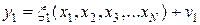
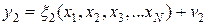
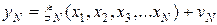
Этап определения параметров по минимуму данных подразумевает выбор из фундаментальной системы уравнений числа уравнений, совпадающих с числом неизвестных по которым эти данные определяются, например методом итераций. Полученные параметры используются далее для линеаризации уравнений измерений при обработке избыточных измерений.

Суть линеаризации заключается в разложении уравнений измерений в ряд Тейлора

и представлении фундаментальной системы уравнений в виде

Где ,

Обозначив для краткости фундаментальную систему можно также записать как

Следует отметить, что после линеаризации обработка избыточных измерений может быть сведена к оценке приращений с последующей выработкой искомых параметров как

Где номер итерации.

При обработке избыточных измерений обычно задаются некоторым функционалом невязок

и определяют оценку параметров, минимизирующих этот функционал.

Во многих случаях до проведения опыта возможно предсказать вид закона распределения. Как правило, используются предельные теоремы теории вероятностей. Среди множества предельных теорем для теории ошибок наибольшее значение имеет теорема Ляпунова, утверждающая, что сумма независимых величин в пределе распределена по нормальному закону.

Оценки и их классификация

Формально в качестве оценки неизвестного параметра может рассматриваться любая функция измерений .

Качество оценки определяется ее свойствами:

Несмещенностью, состоятельностью, эффективностью.

Несмещенность

Оценка параметра называется несмещенной,если выполняется условие

,

Где -оценка случайной величины .

Состоятельность

, Оценка параметра называется состоятельной,еслис ростом числа опытов она сходится по вероятности к параметру .

.

Эффективность

Оценка параметра называется эффективной,если она обладает минимальной дисперсией, т.е.

где -ковариационная матрица эффективной оценки, -ковариационная матрица любой другой оценки,

Насколько точно можно оценить неизвестные параметры? Неравенство Рао-Крамера.

Неравенство показывает, насколько точно можно оценить неизвестные параметры по ограниченной выборке.

Выведем это неравенство для несмещенной оценки

Для несмещенной оценки имеет место соотношение

где - условная плотность совместного распределения величин .

Продифференцировав это выражение по , получим

откуда следует, что

.

Применяя к этому выражению неравенство Коши-Буняковского получим

Заметим, что в правой части первый интеграл представляет собой по определению дисперсию

и, как следствие имеем

Можно показать, что знак равенства

имеет место только в случае, когда

.

Величину, стоящую в знаменателе

Р. Фишер назвал информацией, содержащейся в выборке.

Если предположить, что измерения независимы и равноточны, имеем

= и неравенство информации можно записать в виде

Пример. Пусть производится оценка математического ожидания нормального распределения

В этом случае

Следовательно, в рассматриваемом примере дисперсия любой регулярной оценки удовлетворяет неравенству

,

но это дисперсия среднего арифметического, распределенного по нормальному закону. Это означает, что среднее арифметическое является эффективной оценкой математического ожидания.

Классификация оценок по методам их получения.

Различают два случая: когда известна плотность распределения случайной величины и когда статистическое описание случайной величины неизвестно. В первом случае получили распространение такие методы как метод наименьших квадратов (МНК) , метод максимального правдоподобия, метод наименьших модулей (МНМ), метод моментов, байесовский метод. В рамках этих методов лежит рассмотрение совместной плотности измерений и оцениваемых параметров, позволяющих в ряде случаев получать оптимальные оценки путем минимизации соответствующих функционалов, зависящих от плотности.

Например, если задать функционал

и решитьзадачу минимизации этого функционала, то такая задача обеспечивает получение оценки с минимумом среднего квадрата ошибки вектора состояния

Ко второму случаю относятся методы, которые не предполагают знания плотности распределения и рассматриваются просто как некоторые удобные вычислительные процедуры получения оценок.

Рассмотрим вначале вычислительные методы, в частности, метод наименьших квадратов. В рамках этого метода функционал, подлежащий минимизации задается в виде

где -вектор ошибок измерений, -величина называемая невязкой ошибок измерений.

Как следствие, в рамах этой задачи определяется такое значение принимаемое далее за оценку этого вектора, которое минимизирует сумму квадратов невязок.

Метод, в рамках которого достигается получение этой оценки получил название метода наименьших квадратов( МНК).(least square method) (LSM)

Оценку полученную по МНК можно записать в виде

Для того, чтобы определить минимум функционала

Нужно взять частные производные по каждой компоненте вектора

И получить систему уравнений, получивших название нормальных

(*)

Решая такую систему по методу итераций, можно найти требуемую оценку вектора следует иметь в виду, что решение уравнений (*) могут соответствовать точкам перегиба, а метод итераций сходится к точкам локальных минимумов.

Заметим, что в рамках метода наименьших квадратов рассматривается также критерий , отражающий разную точность получения измерений

где матрица ошибок измерений Если матрица ошибок измерений диагональна

минимизируемый критерий можно представить в виде

В этом случае говорят об обобщенном методе наименьших квадратов (ОМНК)

В ряде случаев при обработке методом наименьших квадратов используют априорную информацию, для чего фундаментальную систему уравнений

Дополняют уравнениями

где параметр отражает неточность априорной информеции Если эту неточность охарактеризовать матрицей вторых центральных моментов выражения, используемые в методе наименьших квадратов модефицируются и принимают вид

которая при диагональнах матрицах и примут вид

где диагональные элементы матрицы

Такой метод наименьших квадратов получил название модифицированного метода наименьших квадратов.

Рассмотрим теперь частный случай фундаментальной системы измерений а именно случай линейных измерений

В этом случае

И система нормальных уравнений примет вид

Решая эту систему уравнений, получим выражение для оценки

Для получения оценки в рамках ОМНК запишем

откуда можно получить следующую систему нормальных уравнений

откуда

Для получения оценки в рамках ММНК рассмотрим функционал

Проводя несложные преобразования, можно получить следующее выражение для оценки