Пример 1. Найдите производную функций:

Найдите производную функций:

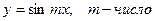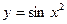а) ; б) ; в)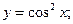

г) .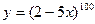

Решение.

а) Данная функция является сложной функцией: 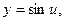где 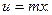Тогда

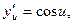
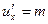и .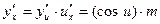

Заменив u на mx, окончательно получим .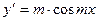

б) Полагая 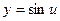, где 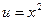, и применяя правило дифференцирования сложной функции, имеет:

.

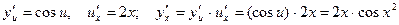в) Здесь 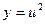, где .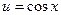

Имеем ;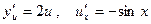

.

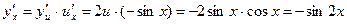г) 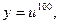где 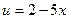. Имеем , .

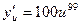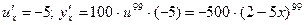Пример 2.

Найдите производную функции .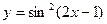

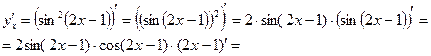
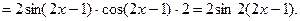
Дифференцирование обратной функции.

Пусть 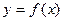(1)

есть дифференцируемая функция от аргумента x в некотором интервале (a,b).Если в уравнении (1) y рассматривать как аргумент,а x как функцию, то эта новая функция 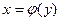, где 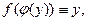называется ,как мы знаем, обратной по отношению к данной.Нашей задачей является: зная производную 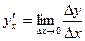функции 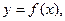найти производную 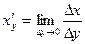обратной ей функции 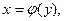предполагая ,что обратная функция существует и непрерывна в соответствующем промежутке.