Ақырсыз функцияның меншіксіз интегралы

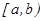Айталық, функциясы аралығында үзіліссіз, ал 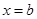нүктесінде ақырсыз болсы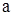н. -дан 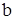- ның сол жағына дейін осы функциядан алынған меншіксіз интеграл деп сол жақ шекті айтады.

.

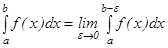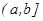Егер функциясы аралығында үзіліссіз, ал 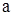нүктесінде үзілісті болса, онда 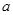-ның оң жағынан 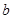-ға дейінгі осы функцияның меншікті интегралы деп мына оң жақ шекті айтады

.

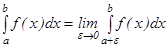6- мысал. 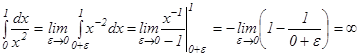,яғни, интеграл жинақсыз.

Мына меншіксіз интегралдардың жазылуы жақсылық емес (зұлымдық), себебі үзіліссіз функциялардың анықталған интегралдарынан айырмашылығы жоқ.

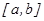Айталық, функциясы аралығындағы 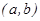интервалының үзіліске ұшырайтын 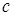нүктесінен басқа жерлерінде үзіліссіз болсын. Сонда осы кесіндіден алынған меншіксіз интегралы деп келесі екі меншіксіз интегралдардың қосындысын айтамыз.

.

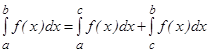Оң жағындағы екі интеграл жинақты болса, онда мұндай интегралды жинақты деп атайды.

Әдебиеттер: 1 нег.[407-436], 11 қос. [506-510], [515-526].

Бақылау сұрақтар:

1. Анықталған интегралды қолданып, жазық фигураның аудандарын есептеу.

2. Қисық доғаның ұзындығын табу.

3. Айналу денесінің көлемін есептеу.

4. Меншіксіз интегралдың түрлерін атаңыз.

Дәріс.

Дәріс тақырыбы:Анықталған интегралдың қолданылуы

Дәріс жоспары:

§ Жазық фигураның ауданын табу.

§ Поляр координаттарындағы аудан.

§ Қисық доғасының ұзындығы.

§ Айналу бетінің ауданын табу.

§ Меншіксіз интегралдар.

§ Әдебиеттер.

§ Бақылау сұрақтары.

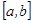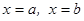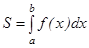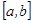а) функциясы кесіндісінде теріс емес және үзіліссіз болсын. Онда жоғарыдан функциясының графигімен, төменнен өсімен, ал бүйір жақтарынан түзулерімен қоршалған қисық сызықты трапецияның ауданы интегралына тең болады, яғни Егер кесіндісінде 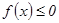болса, онда қисық сызықты трапеция өсінің төменгі жағына орналасқан және 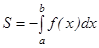болады.

1-мысал. 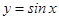синусоидасымен және 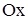осімен шектелген фигураның ауданын табу керек ( ).

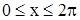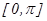аралығында 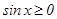, ал 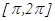аралығында 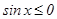болғандықтан, берілген облыстың ауданын табайық

.

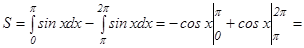
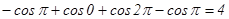б) 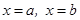түзулерімен және 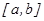аралығында үзіліссіз 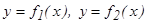(мұндағы 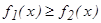) функциялардың графиктерімен шектелген фигураның ауданы мына формуламен табылады.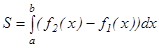

в) Егер 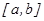кесіндісінде функциясының графигі параметрлік функция түрінде берілсін 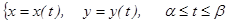мұндағы 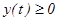үзіліссіз, ал 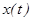функциясы 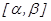кесіндісінде бір сарынды, үзіліссіз дифференциалданатын функция, ал 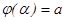, 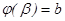болса, онда қисық сызықты трапецияның ауданы мына формуламен табылады .

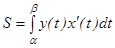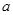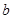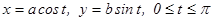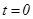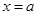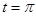2−мысал. Жарты өстері және болатын эллипстің жоғарғы жағындағы жарты бөлігінің параметрлік теңдеуі былай беріледі: . Егер десек, онда , ал десек 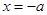тең болады. Сонда эллипстің ауданы былай табылады

.

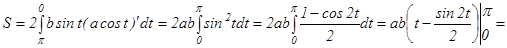
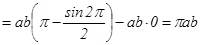Поляр координаттарындағы аудан.Координат төбесінен шығатын сәулелермен 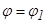және 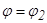(мұндағы 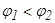) және теріс емес 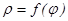функциясының 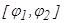кесіндідегі үзіліссіз графигімен шектелген қисықсызықты үшбұрыштың ауданы мына формуламен есептелінеді: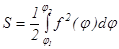

3-мысал. 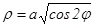қисығымен шенелген облыстың ауданын табамыз. Бұл қисық Бернулли лемнискатасы деп аталады.

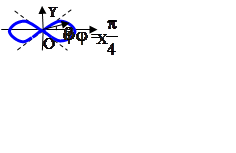
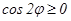шартынан интегралдау облысы табылады. Осыдан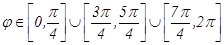 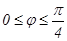үшін бүкіл облыстың 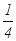-ін құрайды.

.
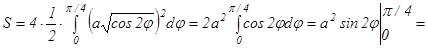
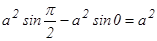