Существует определение: говорят, что a<b, если разность a-b<0. Ищем в ответах отрицательное число. Это ответ D) -5.

5. Найдите наименьшее целое решение неравенства 9^7-x≤27. Решаем. Представим обе части неравенства в виде степеней числа 3. Получаем:

3^2(7-x)≤3³. Так как показательная функция с основанием 3 является возрастающей, то, опуская основания степени, сохраним знак неравенства: 2(7-x)≤3,

раскрываем скобки: 14-2x≤3. Упрощаем: -2x≤-11 и делим обе части неравенства на (-2), при этом знак неравенства меняется на противоположный: x≥5,5. Наименьшее целое число, принадлежащее промежутку [5,5; +∞) - это число 6.

6. Вычислите: sin15°·cos15°. Применим формулуsin2α=2sinαcosα.

sin15°·cos15°=(1/2)sin30°=(1/2)·(1/2)=1/4.

7. Найдите значение производной функции y(x_o), если y(x)=3lnx-x², x_o=1. Решаем. Найдем производную функции y(x) и подставим вместо х значение x_o=1.

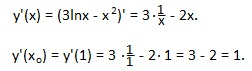
8. Углы параллелограмма пропорциональны числам 9 и 3. Чему равна разность двух углов, прилежащих к одной стороне параллелограмма? Решаем. Обозначим одну часть через х. Тогда углы параллелограмма 9х и 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне, равна 180°, составим уравнение:

9х+3х=180, отсюда 12х=180. Делим обе части на 12 и получаем х=15. Требуется найти разность углов параллелограмма. В частях это 9х-3х=6х. Так как х=15, то искомая разность углов равна 6·15°=90°.

9. Радиусы двух шаров относятся как2:3. Как относятся их площади поверхности? Отвечаем. 1) Все шары подобны. 2) Площади подобных фигур относятся как квадраты их линейных размеров. Площади поверхностей будут относиться как

2²:3², т. е. как 4:9.

10. При каких значенияхk уравнение 2x²+kx+18=0 имеет один корень? Решаем. Квадратное уравнение имеет единственный корень (два равных корня), если дискриминант D=0. Составляем выражение D=b²-4ac. Для наших значенийa=2, b=k, c=18 получаем D=k²-4∙2∙18=k²-144. Так как должно выполняться условие D=0, то получим уравнение k²-144=0, отсюда k²=144, в результате k=±12.

11. Решим первое уравнение системы. Так как 25=5², то опустив основания степени и приравняв показатели, получаем равенство: |x-1|=2. Тогда либо х-1=2⇒х=3, либо х-1=-2⇒х=-1 (модули чисел 2 и (-2) равны двум). Полученные значения х подставляем во второе уравнение системы (х+у=3). Если х=3, то у=0; если х=-1, тоу=4. Решением системы будут пары значений х и у: (3; 0) и (-1; 4).

12. Найдите произведение корней уравнения:

13. Данное уравнение не имеет корней, так как квадрат любого числа (у нас квадрат суммы синуса и косинуса) не может быть равен отрицательному числу.

14. Последовательность, заданная формулой a_n=5+2n, является арифметической прогрессией. Найдите сумму ее первых двенадцати членов. Решаем. Воспользуемся следующей формулой суммы n первых членов арифметической прогрессии:

15. Найдите область определения функции:

16. Найдите производную функции y(x)=sine^x. Решаем. Нам дан синус. Производная синуса - это косинус. Так как аргумент у синуса был сложный, то находим производную e^x и умножаем на косинус. Итак, y’(x)=cose^x∙(e^x)’=e^x∙cose^x.

17. Найти площадь круга, если длина окружности равна 8π см. Решаем. Чтобы найти площадь круга по формуле S=πR², нам нужно знать радиус круга R. Длина окружности, вычисляемая по формуле С=2πR, по условию, равна 8π. Тогда радиус круга R=8π:2π=4 (см). Искомая площадь круга S=π∙4²=16π (см²).

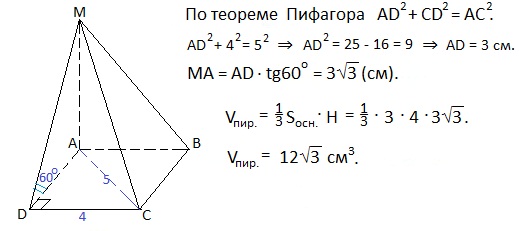
18. Задача на пирамиду. Основание пирамиды MABCD - прямоугольник ABCD. МА перпендикулярно (АВС). Если АС=5 см, угол MDA равен 60°, то найдите МА и объем пирамиды.

19. Найдите координаты точек пересечения прямой у=-х+9 и данной окружности. Решаем. Подставим значение у в уравнение окружности. (x-6)²+(-x+9-6)²=3²∙5. Упростим: (x-6)²+(3-x)²=45; раскроем скобки: x²-12x+36+9-6x+x²=45; перенесем число 45 в левую часть (не забыв поменять знак) и приведем подобные слагаемые: 2x²-18x=0. Решаем полученное неполное квадратное уравнение 2x(x-9)=0. Получаем: x=0 и x=9. Тогда, подставив эти значения в уравнение прямой у=-х+9, получаем: y=9 и y=0. Точки пересечения прямой и окружности: (0; 9) и (9; 0).

20. Вычислить:

21. Найдите значение выражения:

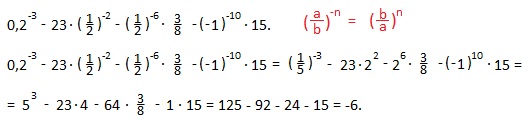
22. Решить уравнение:

23. Решить уравнение: sinx+sin5x+cosx+cos5x=0. Решаем. Сгруппируем слагаемые: (sin5x+sinx)+(cos5x+cosx)=0 и применим формулы преобразования суммы синусов и суммы косинусов в произведение.

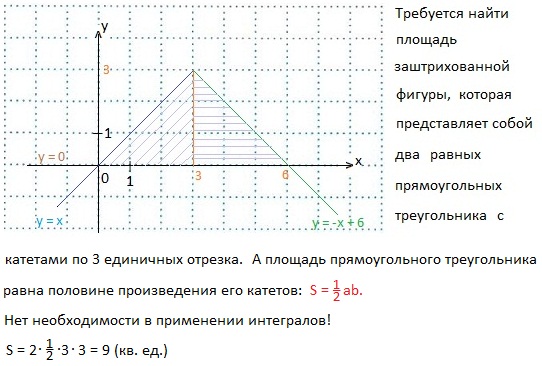
24. Найдите площадь фигуры, ограниченной графиком функции y=3-|x-3| и прямой у=0. Решаем. Прямая у=0 - это ось Ох. Построим график функции y=3-|x-3|. Для этого нам нужно освободиться от модульных скобок, и освобождаться мы будем по определению модуля числа а: |a|=a, если a≥0; |a|=-a, если a<0.

1) Если х-3≥0, т.е. если х≥3, то функция примет вид: у=3-(х-3)=3-х+3=-х+6. Следовательно, на промежутке [3; +∞) нужно строить прямую у=-х+6.

2) Если х-3<0, т.е. если x<3, то функция примет вид: у=3+(х-3)=3+х-3=х. Следовательно, на промежутке (-∞; 3] нужно строить прямую у=х.

25. Человек говорит: «Я прожил 50 лет, 50 месяцев, 50 недель, 50 дней и 50 часов». Сколько ему лет? Рассуждаем. Мы знаем, что год состоит из 12 месяцев, поэтому от 50 месяцев возьмем 48 месяцев = 4 года и добавим к 50 годам, получается 54 года. А сколько осталось? 2 месяца (от 50 месяцев) плюс 50 недель плюс 50 дней плюс 50 часов. Потянет это на один год? Да, так как год состоит примерно из 52 недель (52 недели умножим на 7 дней и получим 364 дня). Добавим к 54 годам еще один год. Ответ: человеку55 лет.