Основные теоретические положения. Основной задачей статистической обработки является определение или подтверждение 1-ого из законов распределения случайной величины и получение точечных и
Основной задачей статистической обработки является определение или подтверждение 1-ого из законов распределения случайной величины и получение точечных и интервальных значений показателей надежности.
Для многих систем уже существуют сформировавшиеся прототипы законов, с помощью которых производится оценка показателей надежности. Для периода нормальной эксплуатации проверяется подтверждение экспоненциального закона надежности.
При определении и подтверждении закона распределения производится построение гистограмм для интенсивности отказов и вероятности безотказной работы. Аппроксимация гистограмм теоретическим законом распределения (экспоненциальным) предполагает выделение периода времени T, на котором не происходит значительного роста интенсивности отказов (который свидетельствует о проявлении износовых отказов). На этом отрезке времени вычисляется сначала средняя интенсивность отказов, а затем точечная оценка среднего времени наработки до первого отказа 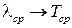 .
.
Проверка допустимости закона распределения предполагает использование критерия согласия и, как правило, используется критерий согласия Колмогорова
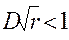 ,
,
r – число отказов к моменту времени T, D – максимальное отклонение (по модулю) статистической вероятности безотказной работы от теоретической, при выполнении которого предположение о допустимости закона распределения является верным.
При вычислении интервальной оценки наработки до первого отказа назначается доверительная вероятность a – это вероятность того, что Tср не выйдет за пределы доверительного интервала
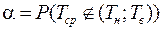 .
.
Tн, Tв определяются по уровню значимости β = 1 – α
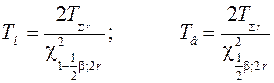
2r – число степеней свободы для вероятностей
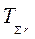 – суммарная наработка до отказа по отказам, зафиксированным во время эксперимента
– суммарная наработка до отказа по отказам, зафиксированным во время эксперимента
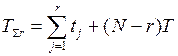
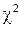 - определяется по таблице.
- определяется по таблице.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими положениями по анализу показателей надежности по статистическим данным.
2. Решить задачу, приведенную ниже, в соответствии с номером варианта.
Задания для лабораторной работы
Вариант №1
В результате испытаний 100 кинескопов, проводившихся в течение 12000 час, получены следующие данные о наработках до отказа.
| Dti, ч. | 0–2000 | 2000–4000 | 4000–6000 | 6000–8000 | 8000–10000 | 10000–12000 |
| ni |
Построить гистограммы для l* и P*. Определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,2.
Вариант №2
В результате наблюдения за 200 телевизорами одной модели, были получены данные до первого отказа всех 200 телевизоров (см. табл.).
| Dti, т.ч. | 0 – 5 | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,1.
Вариант №3
В результате наблюдения за 45 образцами радиоэлектронного оборудования, получены данные до первого отказа всех 45 образцов, сведенные в табл.
| Dti, т.ч. | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,1.
Вариант №4
В результате наблюдения за 50 энергосберегающими лампами, были получены данные до первого отказа всех 50 ламп (см. табл.).
| Dti, т.ч. | 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,2.
Вариант №5
В результате испытаний 100 микросхем, проводившихся в течение 1200 ч, получены следующие данные о наработках до отказа.
| Dti, ч. | 0–200 | 200–400 | 400 – 600 | 600–800 | 800–1000 | 1000–1200 |
| ni |
Построить гистограммы для l* и P*. Определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,2.
Вариант №6
В результате наблюдения за 50 электронными осциллографами, были получены данные до первого отказа всех 50 осциллографов (см. табл.).
| Dti, т.ч. | 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,1.
Вариант №7
В результате наблюдения за 60 электрическими генераторами, были получены данные до первого отказа всех 60 машин (см. табл.)
| Dti, т.ч. | 0 – 5 | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,05.
Вариант №8
В результате наблюдения за 80 холодильниками, получены данные до первого отказа всех 80 холодильников, сведенные в табл.
| Dti, т.ч. | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,1.
Вариант №9
В результате наблюдения за 145 образцами радиоэлектронного оборудования, получены данные до первого отказа всех 145 образцов, сведенные в табл.
| Dti, т.ч. | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,1.
Вариант №10
В результате наблюдения за 30 электрическими машинами, были получены данные до первого отказа всех 30 машин (см. табл.).
| Dti, т.ч. | 0 – 5 | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 |
| ni |
По полученным данным построить гистограммы для l* и P*. Выделить период нормальной эксплуатации изделий. Для периода нормальной эксплуатации определить среднее время наработки до первого отказа TСР и lСР. Выполнить проверку допустимости экспоненциального закона распределения на основе критерия Колмогорова. Определить интервальную оценку TСР для уровня значимости b = 0,05.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что представляет математическая модель и для каких целей она используется в задачах надежности?
2. Из каких условий выбирается закон распределения наработки до отказа объекта?
3. В чем заключается постановка задачи при испытаниях объектов на надежность?
4. Что представляет собой процедура формирования статистического ряда по результатам испытаний?
5. Какие эмпирические функции рассчитываются при обработке результатов испытаний?
6. В чем заключается выбор закона распределения наработки до отказа по результатам испытаний?
7. Что представляет собой критерий согласия?
Список литературы
1. Черкесов, Г.Н.. Надежность аппаратно-программных комплексов: учебное пособие. – СПб: Питер, 2005.
2. Кон, Е.Л. Надежность и диагностика компонентов инфо-коммуникационных и информационно-управляющих систем: учеб. пособие / Е.Л. Кон, М.М. Кулагина. – Пермь, Изд-во Перм. нац. исслед. политехн. ун-та, 2012 – URL: http://lib.pstu.ru/elib.
3. Бочкарев, С. В.. Диагностика и надежность автоматизированных систем:: учеб. пособие / С. В. Бочкарев, А. И. Цаплин.. – Пермь, Изд-во Перм. нац. исслед. политехн. ун-та, 2008 – URL: http://lib.pstu.ru/elib.
4. Гмурман В.Е.. Руководство к решению задач по теории вероятности и математической статистике: Учеб. пособие для студентов вузов. Изд. 4-е, стер. М.: Высш. шк., 1997. – 400 с.: ил. (Приложения)
