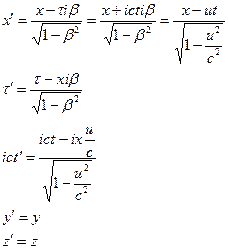Уравнение движения

5) Алгебра 4-векторов

С 4-мерным вектором можно производить те же действия, что и с 3-хмерными векторами в эвклидовой геометрии.

1) При сложении векторов соответствующие компоненты складываются.

Закон сохранения импульса: если несколько частиц , то сум-марный 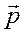до столкновения и после не меняются:

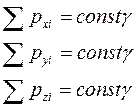
В 4-хмерном мире сумма x, y, z- компонент = const, но определения закона сохранения импульса является не полным. Должна сохраняться и компонента 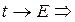в пространстве добавляется закон сохранения энергии.

Вводим обозначения:

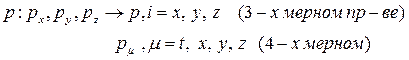
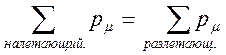
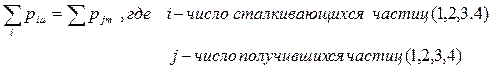
2) Скалярные произведения векторов

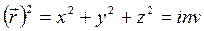- квадрат длины вектора в 3-хмерном пространстве. Квадрат длины интервала:

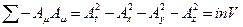- скалярное произведение

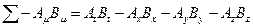
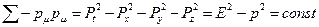в системе координат.

Если движется какой-то объект или частица, то мы можем выбрать систему, которая связана с движущимся объектом. В этой СК объект- частица находится в покое, ;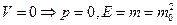

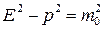
В системе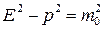

Рассмотрим фотон- частицу, движущуюся со скоростью света:

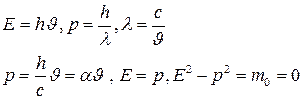
Вывод: масса покоя фотона =0

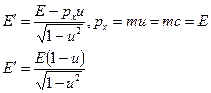
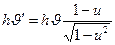- эффект Топплера.

6) Вывод преобразования Лоренца

Введём обозначения Миаковского

Т. Р характеризуется интервалом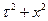

При вращении системы (y-x)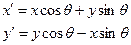

При вращении системы ( )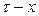

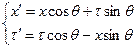(6.1)

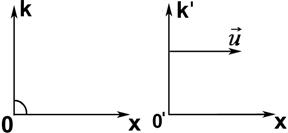
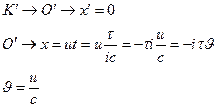
Тогда имеем (6.1) в виде:

;

;
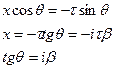
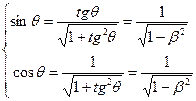